Ответы на вопросы по эконометрике (теория) (шпоры). Автокорреляция случайного возмущения. Причины. Последствия. Алгоритм проверки адекватности парной регрессионной модели
 Скачать 487.3 Kb. Скачать 487.3 Kb.
|
56, 57. Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам.В моделях, нелинейных по параметрам, например степенных или показательных, непосредственное применение МНК для их оценки невозможно, так как необходимым условием применимости МНК является линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование. Логарифмические модели: Y = AXb, где А и b— параметры модели. Прологарифмируем обе части данного уравнения: ln(Y)=ln(A) + b*ln(X) = a+b*ln(X), где а= ln(A) (*). Спецификация, соответствующая (*) называется двойной логарифмической моделью: ln(Y)= a+ b*ln(X)+u, поскольку и эндогенная переменная, и регрессор используются в логарифмической форме. Введем обозначения: Y*=ln(Y), X*=ln(X) Y*=a+b*X+u Получаем спецификацию линейной модели, к которой при соответствующем включении случайного возмущения применим МНК. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Пусть получена МНК-оценка моделиY*=a+b*X+u: y*=ā + bx+u (Sā) (Sb) (Su) Коэффициенты исходной модели и их стандартные ошибки вычисляются с учетом замены. Нелинейный МНК. В общем случае оценка нелинейных по параметрам уравнений выполняется с помощью так называемого нелинейного метода наименьших квадратов (НМНК). Обозначим нелинейное по параметрам уравнение регрессии f(X, ß) (X— матрица рсгрсссоров,ß — вектор параметров). Параметры уравнений в данном методе подбираются таким образом, чтобы максимально приблизить кривую f(X, ß) к результатам наблюдений эндогенной переменной Y. Таким образом, здесь, как и в обычном МНК, минимизируется сумма квадратов отклонений: F= 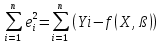 2 (**) 2 (**)Если продифференцировать F по параметрам и приравнять производные нулю, то получим нелинейную систему нормальных уравнений. В случае линейного уравнения регрессии нормальные уравнения представляли собой систему линейных уравнений, решение которой не составляло труда. Нелинейный метод наименьших квадратов сводится к задаче минимизации функции (**) нескольких переменных ß=(ß1,…,ßn) 58.Спецификация моделей со случайными возмущениями и преобразование их к системе нормальных уравнений. Один из принципов спецификации - включение в спецификацию экономической модели случайных возмущений. На практике не всегда удается учесть влияние всех факторов на изучаемую переменную (например, в функции спроса учесть возрастные особенности потребителя), выбрать правильную форму математической зависимости между экономическими переменными (например, нелинейную вместо линейной), безошибочно выполнить измерения (правильно провести опрос). Поэтому необходимо включать некоторые случайные величины, называемые случайные возмущения. Y = f(x)+ε , где f(x)- часть эндогенной переменной, объясняемая значением экзогенной переменной Х; ε – случайное возмущение. Для того чтобы среди множества уравнений регрессии выбрать одно, необходим критерий отбора. При оценивании параметров регрессионных моделей наиболее часто применяется МНК. Его оценки обладают свойствами несмещённости, состоятельности, эффективности: 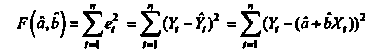 (1) (1)То есть оценки параметров должны быть подобраны таким образом, чтобы сумма квадратов случайных возмущений стремилась к минимуму Для нахождения минимума дифференцируем (1): 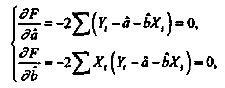 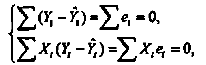 Получаем стандартную форму нормальных уравнений: 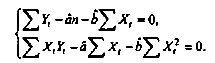 Из которых находим параметры. Из которых находим параметры.59.Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов.Гетеро-сть приводит к неэффективности оценок несмотря на их несмещенность. Это может привести к необоснованным выводам по качеству модели. Поэтому при установлении гетеро-сти возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии отклонений случайных возмущений. Если такие дисперсии известны, применяется метод взвешенных наименьших квадратов (ВНК). Опишем метод ВНК на примере парной регрессии: Разделим обе части на известное СКО: Перейдем к новым переменным: При этом для vi выполняется условие гомоскедастичности: Так как по первой предпосылки МНК 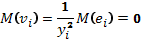 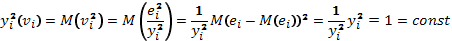 То есть выполняются все предпосылки МНК, то есть все полученные оценки будут наилучшими линейными несмещенными оценками. 60.Статистические свойства оценок параметров парной регрессионной модели Исходя из теоремы Гаусса-Маркова, МНК-оценки параметров парной регрессии обладают следующими свойствами:
61.Статистические характеристики выборки и генеральной совокупности статистических данных. Их соотношения. Генеральная совокупность – это всё множество объектов, обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени, входящих в предмет изучения в соответствии с программой исследования. Выборка (Выборочная совокупность) – часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности. В основе статистических выводов проведенного исследования лежит распределение случайной величины X, наблюдаемые же значения(х1, х2, … ,хn)называются реализациями случайной величины Х (n — объем выборки). Распределение случайной величины X в генеральной совокупности носит теоретический, идеальный характер, а выборочный аналог является эмпирическим распределением. Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому параметры оценивают по эмпирическим данным, а затем их подставляют в аналитическое выражение, описывающее теоретическое распределение. В любом случае восстановленное по выборке эмпирическое распределение лишь грубо характеризует истинное. Важнейшими параметрами распределений являются математическое ожиданиеE(x) и дисперсия 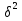 . .По своей природе распределения бывают непрерывными и дискретными. Наиболее известным непрерывным распределением является нормальное. Выборочными аналогами параметров E(x) и 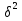 для него являются: среднее значение для него являются: среднее значение 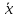 и эмпирическая дисперсия и эмпирическая дисперсия 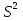 . Среди дискретных в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение. Параметр математического ожидания E(x) этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком X (она обозначена буквой p); доля совокупности, не обладающая этим признаком, обозначается буквой q (q = 1 — p). Дисперсия же . Среди дискретных в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение. Параметр математического ожидания E(x) этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком X (она обозначена буквой p); доля совокупности, не обладающая этим признаком, обозначается буквой q (q = 1 — p). Дисперсия же 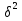 альтернативного распределения также имеет эмпирический аналог альтернативного распределения также имеет эмпирический аналог 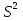 . .В зависимости от вида распределения и от способа отбора единиц совокупности по-разному вычисляются характеристики параметров распределения. Долей выборки kn называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности: kn = n/N. Выборочная доля w — это отношение единиц, обладающих изучаемым признаком x к объему выборки n: w = nn/n. Так как выборочная совокупность отлична от генеральной, то возникают ошибки выборки. Связь: E(Xв(с чертой))=Хо(с чертой). Е(Дв)=((n -1)/³)*До Д(Хв(с чертой))=До/n 62.Схема Гаусса – Маркова В рамках модели (1) 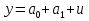 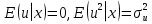 величины выборки (2) 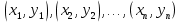 связаны следующей системой линейных алгебраических уравнений: связаны следующей системой линейных алгебраических уравнений: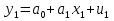 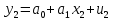 …………………….. 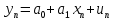 Она называется системой уравнений наблюдений объекта в рамках линейной модели (1), или, иначе, схемой Гаусса – Маркова. Компактная запись: 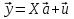 где 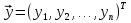 – вектор наблюденных значений эндогенной переменной y модели (1); – вектор наблюденных значений эндогенной переменной y модели (1);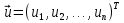 - ненаблюдаемый вектор случайных возмущений (остатков); - ненаблюдаемый вектор случайных возмущений (остатков);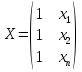 – матрица наблюденных значений предопределенной переменной x модели (1), расширенная (при наличии в функции регрессии определяемого коэффициента – матрица наблюденных значений предопределенной переменной x модели (1), расширенная (при наличии в функции регрессии определяемого коэффициента 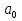 ) столбцом единиц; ) столбцом единиц;Наконец, 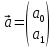 - вектор неизвестных коэффициентов функции регрессии модели, подлежащий оцениванию по выборке (2). - вектор неизвестных коэффициентов функции регрессии модели, подлежащий оцениванию по выборке (2).63.Теорема Гаусса-Маркова Пусть матрица X уравнений наблюдений 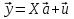 имеет размер имеет размер 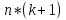 , где , где 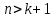 , и обладает линейно-независимыми столбцами, а случайные возмущения , и обладает линейно-независимыми столбцами, а случайные возмущения 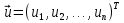 удовлетворяют четырем условиям: удовлетворяют четырем условиям: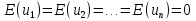 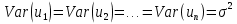 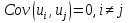 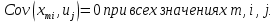 Тогда: А) Наилучшая линейная процедура 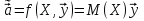 имеет вид: имеет вид: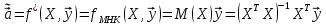 Б) Эффективная линейная несмещенная оценка 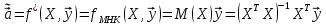 обладает свойством наименьших квадратов: обладает свойством наименьших квадратов: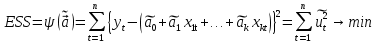 В) Ковариационная матрица оценки 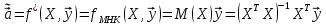 вычисляется по правилу вычисляется по правилу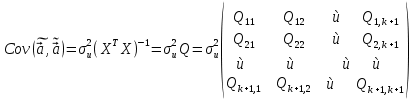 Г) Несмещенная оценка параметра 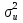 модели находится по формуле модели находится по формуле 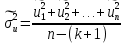 где n – число уравнений наблюдений, k+1 – количество неизвестных коэффициентов функции регрессии модели. 64. Тест ошибочной спецификации Рамсея. Тест Рамсея позволяет проверить, стоит ли начинать поиск дополнительной переменной для включения в уравнение 1. Оценивается уравнение регрессии 2. Вычисляются степени оценок зависимой переменной 3. Оценивается уравнение регрессии с этими степенями 4. Проводится оценка улучшения по F-критерию
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т.е. определяют фактическое значение t-критерия Стьюдента 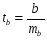 где mb – стандартная ошибка параметра где mb – стандартная ошибка параметра 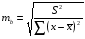 , ,где S остаточная дисперсия на одну степень свободы Данный критерий затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n-2). Этот же результат можно получить после извлечения корня из F-критерия, т.е. tb= 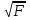 . Аналогично для параметра а. . Аналогично для параметра а. Фактическое значение t-критерия Стьюдента определяется как 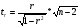 Данная формула свидетельствует о том, что в парной линейной регрессии t2r=F. Кроме того t2b=F, следовательно, t2r= t2b. Таким образом проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о значимости линейного уравнения регрессии. Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт - принимаем или отвергаем гипотезу H0. Если tтабл < tфакт, то H0 отклоняется, т.е. a иbне случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tтабл > tфакт, то гипотеза Ноне откло няется и признается случайная природа формирования a иb. 66, 67. Типы переменных в эконометрических моделях. Структурная и приве дённая формы спецификации эконометрических моделей. Типы переменных: эндогенные – образуются внутри модели. Экзогенные – не зависят от модели, внешние для модели. Модель, возникающая на этапе спецификации, как правило, имеет структурную форму, отражающую заложенные в модель экономические утверждения. В такой форме эндогенные переменные модели, как правило, не выражены явно через ее экзогенные переменные. При помощи алгебраических преобразований модель от структурной формы может быть трансформирована к приведенной форме, где каждая эндогенная переменная представляется в виде явной функции только экзогенных переменных модели. Приведенная форма модели непосредственно предназначена для прогноза (объяснения) эндогенных переменных при помощи экзогенных переменных. В частном случае структурная форма модели может совпадать с приведенной формой. Переход от структурной к приведенной форме возможен всегда и однозначно, а обратное неверно. Приведенная форма. 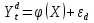 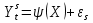 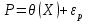 Структурная форма. 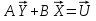 68. Устранение автокорреляции в парной регрессии Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов. Причина – неправильный выбор спецификации модели. Последствия автокорреляции (оценки коэффициентов теряют эффективность, стандартные ошибки коэффициентов занижены). Для устранения автокорреляции можно воспользоваться процедурой Кохрейна-Орката: 1)По выборочным данным выполняется настройка модели и вычисляется вектор остатков регрессии е. 2)По остаткам регрессии оценивается модель авторегрессии: 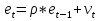 3)С оценкой 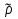 выполняются преобразования (1) и (2). выполняются преобразования (1) и (2).4)Строится новый вектор остатков, и процедура повторяется (начиная с П.2). Итерационный процесс заканчивается при условии совпадения оценок на последней и предпоследней итерациях с заданной степенью точности. 69. F-тест качества спецификации множественной регрессионной модели. Статистикой обсуждаемого ниже критерия гипотезы H0: R2=0 (гипотеза о том что модель абсолютно плохая) против альтернативы H1: 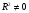 служит случайная переменная: служит случайная переменная: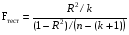 (1) (1)Здесь k — количество регрессоров в модели множественной регрессии, п — объ ем обучающей выборки (у,X),по которой оценена МНК-модель. В ситуации, когда гипотеза H0 справедлива, а слу чайный остаток и в модели обладает нормальным законом распределения, случайная переменная Fтест имеет распределение Фишера с количествами степеней сво боды ν1 и ν2, где ν1=k и ν2=n-(k+1) (2) Данное утверждение положено в основу F-теста. Вот этапы выполнения этой процедуры. 1) вычислить величину (1); 2) задаться уровнем значимости а € (0, 0,05] и при помощи функции FPACПOБP Excel при количествах степеней свободы (2) отыскать (1-α)-квантиль распределения Фишера Fкрит 3) проверить справедливость неравенства F Если оно справедливо, то принять гипотезу H0 и сделать вывод о неудовлетворительном качестве регрессии, т.е. об отсутствии какой-либо объясняющей способности регрессоров в рамках линейной модели. Напротив, когда неравенство (3) несправедливо —следует от клонить гипотезу H0 в пользу альтернативыH1.Другими словами, сделать вывод о том, что качество регрессии удовлетвори тельно, т.е. регрессоры в рамках линейной модели обладают способностью объяснять значения эндогенной переменной у. 70. Фиктивная переменная наклона: назначение; спецификация Фиктивные (искусственные) переменные (dummyvariables)- это переменные с дискретным множеством значений, которые количественным образом описывают качественные признаки. В регрессионных моделях применяются фиктивные переменные двух типов: переменные сдвига и переменные наклона. Фиктивная переменная наклона изменяет наклон линии регрессии. При помощи фиктивных переменных наклона можно построить кусочно-линейные модели, которые позволяют учесть структурные изменения в экономических процессах (например, введение новых правовых или нало говых ограничений, изменение политической ситуации и т. д.). Спецификация регрессионной модели в этом случае (например, для парной регрессионной модели, для простоты) имеет вид: 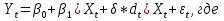 0 – до структурных изменений dt = 1 – после структурных изменений, dt - бинарная переменная Фиктивная переменная входит в уравнение в мультипликативной форме. 71.Функция регрессии как оптимальный прогноз Конечной целью статистического анализа временных рядов является прогнозирование будущих значений исследуемого показателя. Различают д/ср и кр/ср прогнозирование. В первом анализируется долговременная динамика исследуемого процесса, и главным считается выделение общего направления его изменения (тренда). Для предсказания кр/ср колебаний проводится более детальный регрессионный анализ с целью выявления большого числа показателей, определяющих поведение исследуемой величины. Пусть оценивается модель вида Y^t = b0+b1*xt в момент времени ( 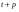 ). Значение Y^t+p – значение по уравнению регрессии, построенному по МНК. Тогда доверительный интервал для действительного значения ). Значение Y^t+p – значение по уравнению регрессии, построенному по МНК. Тогда доверительный интервал для действительного значения 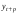 множественной регрессии имеет вид: множественной регрессии имеет вид: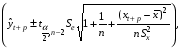 где 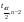 – критическое значение, определяемое для соответствующего уровня значимости – критическое значение, определяемое для соответствующего уровня значимости  и числа степеней свободы и числа степеней свободы 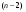 ; ; 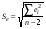 – стандартная ошибка оценки (стандартная ошибка регрессии); – стандартная ошибка оценки (стандартная ошибка регрессии); 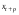 – значение объясняющей переменной в момент ( – значение объясняющей переменной в момент (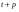 ); ); 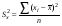 – дисперсия переменной – дисперсия переменной 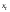 . . После получения прогнозных значений необходимо проверить качество прогноза. Для этого используются следующие показатели: |
