деньгт. Вариант 13. Контрольное задание по финансовой математике
 Скачать 31.47 Kb. Скачать 31.47 Kb.
|
Контрольное задание по финансовой математикеВариант № 131. Цена товара в этом году уменьшилась на 48 руб., что составляет 12% от цены прошлого года. Определить современную стоимость товара. Решение: Для решения задачи запишем пропорцию: 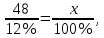 где в качестве переменной x обозначена цена товара в прошлом году 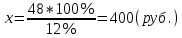 По условию цена в текущем году уменьшилась на 48 руб., значит цена текущего года составляет 352 руб. (400 – 48) Ответ: современная стоимость товара 352 руб. 2. Ссуда в размере 40000 руб. была выдана на 9 месяца под 16% годовых. Какую сумму заплатит должник в конце срока? (Простые проценты) Решение: Формула простых процентов: 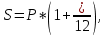 где S – наращенная сумма; Р – первоначальная сумма долга; i – ставка наращения процентов; n – период дисконтирования (количество месяцев). Подставим имеющиеся значения: 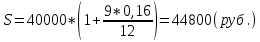 Ответ: в конце срока должник заплатит 44 800 руб. 3. Какова была годовая ставка простых процентов, если сумма в 30000 руб. увеличилась за 2 года на 6000 руб.?Решение: Запишем формулу простых процентов: 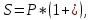 где S – наращенная сумма; Р – первоначальная сумма долга; i – ставка наращения процентов; n – период дисконтирования. Подставим имеющиеся значения: 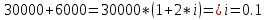 (10%) (10%)Ответ:годовая ставка равна 10% 4. Определить период удвоения вклада при начислении сложных процентов с годовой ставкой 15%.Решение: Формула сложных процентов: 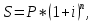 где S – наращенная сумма; Р – первоначальная сумма вклада; i – ставка наращения процентов; n – период дисконтирования. По условию задачи величина вклада удвоилась, значит S = 2P. Подставим имеющиеся значения в формулу: 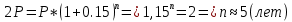 Ответ: период удвоения вклада равен 5 годам 5. Какую сумму надо положить на накопительный счет сегодня, чтобы при годовой ставке сложных процентов i = 16% приобрести через 3 года автомобиль стоимостью 12000 долл.? Решение: Формула сложных процентов: 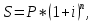 где S – наращенная сумма; Р – первоначальная сумма вклада; i – ставка наращения процентов; n – период дисконтирования. Подставим имеющиеся значения в формулу: 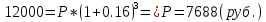 Ответ: на накопительный счет под 16% годовых нужно разместить 7688 руб. 6. Какова была годовая учетная ставка, если вексель на сумму 20000 руб. был учтен в банке за три месяца до срока платежа по цене 19000 руб.? Решение: 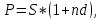 где d–годовая учетная ставка. Подставим имеющиеся данные: 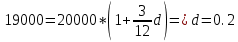 (20%) (20%)Ответ: годовая учетная ставка векселя 20% 7. Какой величины достигнет долг, равный 30000 руб. через 10 лет при росте по сложной ставке 5% годовых? Решение: Формула сложных процентов: 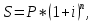 где S – наращенная сумма; Р – первоначальная сумма долга; i – ставка наращения процентов; n – период дисконтирования. 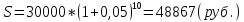 Ответ: через 10 лет долг достигнет величины 48 867 руб. 8. Определить коэффициент наращения при ежеквартальном начислении сложных процентов с номинальной годовой ставкой 20% в течение одного года. Решение: Формула сложных процентов при ежеквартальном начислении процентов: 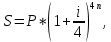 где S – наращенная сумма; Р – первоначальная сумма долга; i – ставка наращения процентов; n – период дисконтирования (в годах). 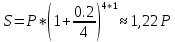 Коэффициент наращения равен отношению наращенной и первоначальной суммы – 1,22. Ответ: коэффициент наращения равен 1,22. 9. 01.03.15 был выдан вексель на 100 000 руб. с обязательством выплатить указанную сумму 20.12.15 с процентами по ставке 15% в год. 20.07.15 вексель был продан банку с дисконтом по годовой учетной ставке 20%. По какой цене вексель был куплен банком? (Обыкновенные проценты с точным числом дней). Решение: Цена векселя – это его номинал за вычетом дисконта. Будущая стоимость векселя по формуле простых процентов с точным числом дней: 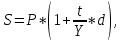 где t - количество дней до срока погашения векселя; Y – количество дней в году (360); d –годовая учетная ставка. Подставим в формулу имеющиеся данные: 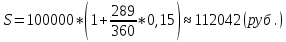 Дисконт банка: 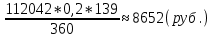 Цена векселя: 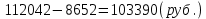 Ответ: вексель был куплен банком за 103390 руб. 10. Пенсионер в течение трех с половиной лет пополнял свой счет в банке в конце каждого месяца на 7000 руб. Определить накопленную пенсионером сумму, если годовая процентная ставка банка составляет 16% и проценты начисляются ежемесячно. Решение: Формула сложных процентов при ежемесячном начислении: 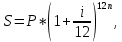 где S – наращенная сумма; Р – первоначальная сумма вклада; i – ставка наращения процентов; n – период дисконтирования (лет). Составим расчетную таблицу:
Ответ: накопленная сумма равна 402917,6 руб. |

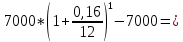 93,3
93,3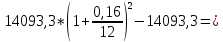 187,9
187,9