Экзамен задачи. Решение Наращенную сумму определим по формуле где s наращенная сумма p первоначальная сумма
 Скачать 24.71 Kb.
|
|
1. Найти сумму накопленного долга и проценты, если ссуда 2280000 руб. выдана на три года под простые 17% годовых. Во сколько раз увеличится наращенная сумма при увеличении ставки на 2%? (10 баллов) Дано: P = 2280000 руб., |n = 3 года, i1 = 17% = 0,17, i2 = 19% = 0,19 Найти: S1 < S2 Решение: Наращенную сумму определим по формуле: 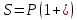 где S – наращенная сумма; P – первоначальная сумма; i – процентная ставка n- срок 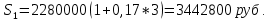 Проценты будут равны I = 3442800 – 2280000 = 1162800 руб. 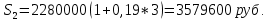 Проценты будут равны I = 3579600 – 2280000 = 1299600руб. Определим во сколько раз увеличится наращенная сумма 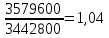 Ответ: в 1,04 раза наращенная сумма увеличится при увеличении ставки на 2% 2. Найти простую процентную ставку  , эквивалентную сложной ставке 8% при сроке 3 года. Ответ привести в процентах с точностью до 0,01. (10 баллов) Дано: ic = 8% = 0,08, n = 3 года Найти: iп Решение: Простую ставку определим по формуле 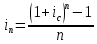 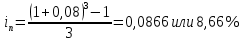 Ответ: простая ставка равна 8,66% 3. Какую сумму нужно положить в банк под 10% годовых мужчине 57 лет, чтобы по достижении им пенсионного возраста 60 лет в течение 15 лет в начале каждого месяца снимать по 25000 рублей, если проценты капитализируются: в конце года; в конце каждого полугодия; в конце каждого квартала; в конце каждого месяца? (10 баллов) Дано: i = 10% = 0,1, n = 3 года, n = 15 лет, R = 25000 руб. Найти: P 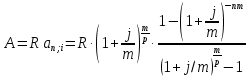 где R - размер годового платежа; j – процентная ставка; n – срок ренты в годах; m – периодичность начисления процентов 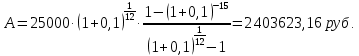 То есть 2403623.16 руб. должно находиться на вкладе по достижении им пенсионного возраста 60 лет. 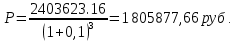 Таким образом, мужчине необходимо положить в банк 1805877.66 руб. В конце каждого полугодия 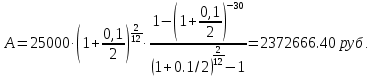 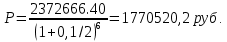 В конце каждого квартала 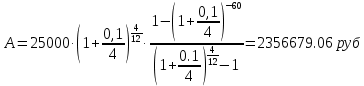 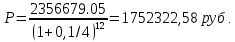 В конце каждого месяца 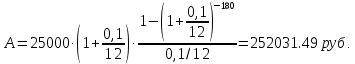 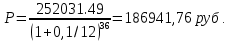 4. Какова простая ставка процентов, при которой первоначальный капитал в размере 4500000 руб., достигнет через 160 дней 4865000 руб.? Число дней году считается приближённо и равно 360. Ответ привести с точностью до 0,01%. (10 баллов) Дано: P = 4500000 руб., t = 160 дней, S = 4865000 руб., T = 360 дней Найти: i Решение: Простую ставку процентов определим по формуле 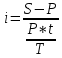 где S – наращенная сумма; P – первоначальная сумма; i – процентная ставка n- срок 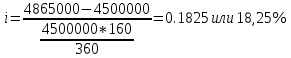 Ответ: ставка простых процентов равна 18,25% 5. Найдите величину дисконта облигации со сроком обращения 5 лет, номинальной стоимостью N=1200 у.е. и купонными выплатами 120 у.е. в конце каждого года, если облигация продаётся в настоящий момент времени по цене 1000 у.е., а процентная ставка составляет 8%. (10 баллов) Дано: N = 1200 у.е, С = 120 у.е., n = 5 лет, i = 8%, P = 1000 у.е. Найти: D Решение: Сначала определим курсовую стоимость облигации: 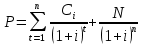 Где N – номинал облигации; C – купон; i – процентная ставка; n – срок 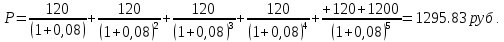 D = 1295.83 – 1000 = 295.83 руб. Ответ: дисконт равен 295,83 руб. 6. Найти сложную процентную ставку 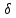 , эквивалентную непрерывной ставке 7%. Ответ привести с точностью до 0,01%. (10 баллов) Дано:  = 7% = 0,07Найти: ic Решение: Эквивалентную сложную процентную ставку определим по формуле:   Ответ: сложная процентная ставка равна 7,25% |