КОНТРОЛЬНОЕ ЗАДАНИЕ ПО ОП.08 Теория алгоритмов для студентов заочной формы обучения специальности 09.02.03 Программирование в ко. КОНТРОЛЬНОЕ ЗАДАНИЕ ПО ОП.08 Теория алгоритмов для студентов зао. Контрольное задание по оп. 08 Теория алгоритмов
 Скачать 217.5 Kb. Скачать 217.5 Kb.
|
1 2 Задание 5. Выполнить задание согласно варианту. Вариант 1. Составить алгоритм нахождения значения функции у= 5/х-1. Вариант 2. Составить блок-схему нахождения корней квадратного уравнения. Вариант 3. Составить схему алгоритма для вычисления значений функции Вариант 4. Составить алгоритм вычисления значений функции 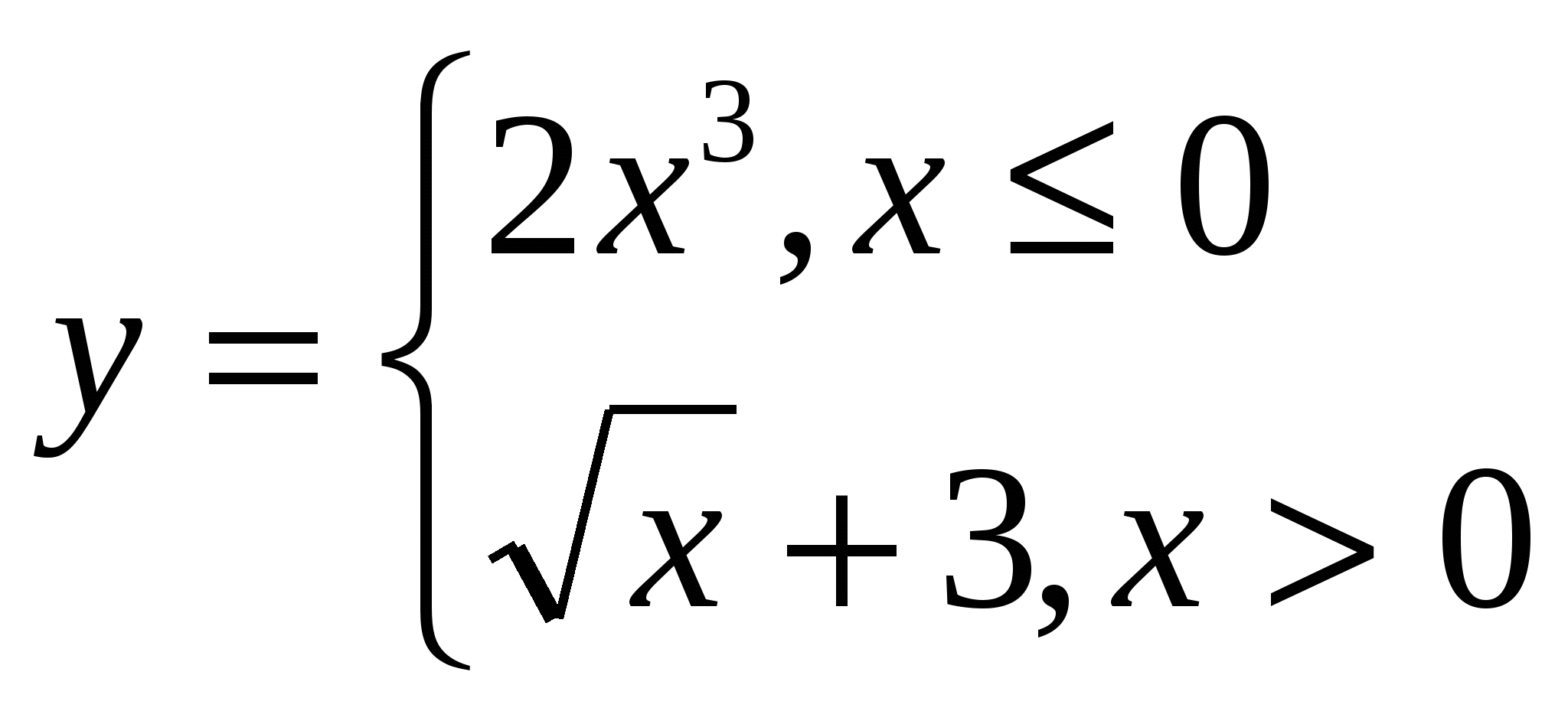 для всех x. для всех x.Вариант 5. Составить алгоритм вычисления значений функции Вариант 6. Составить алгоритм вычисления значений функции 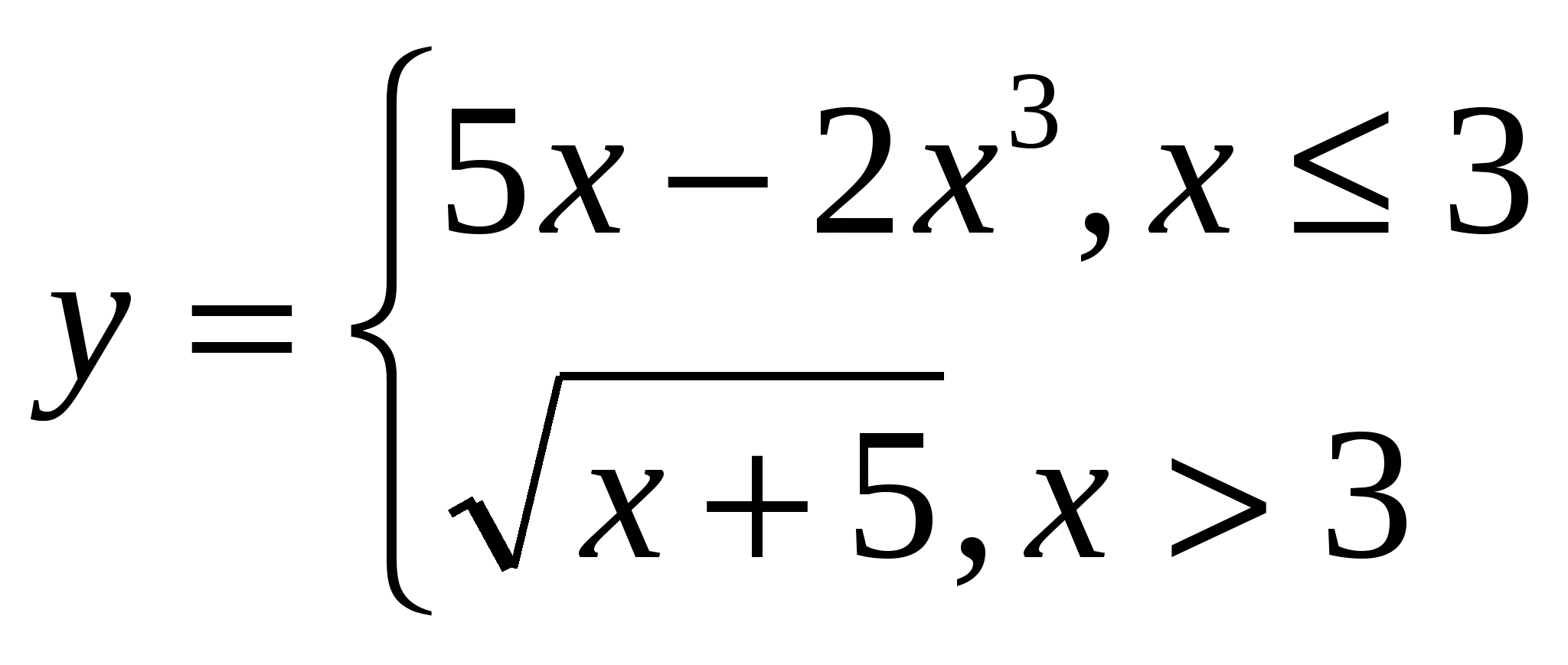 для всех x, принадлежащих отрезку [-8,8], с шагом 1. Записать его в виде блок-схемы. для всех x, принадлежащих отрезку [-8,8], с шагом 1. Записать его в виде блок-схемы.Вариант 7. Составить алгоритм вычисления значений функции 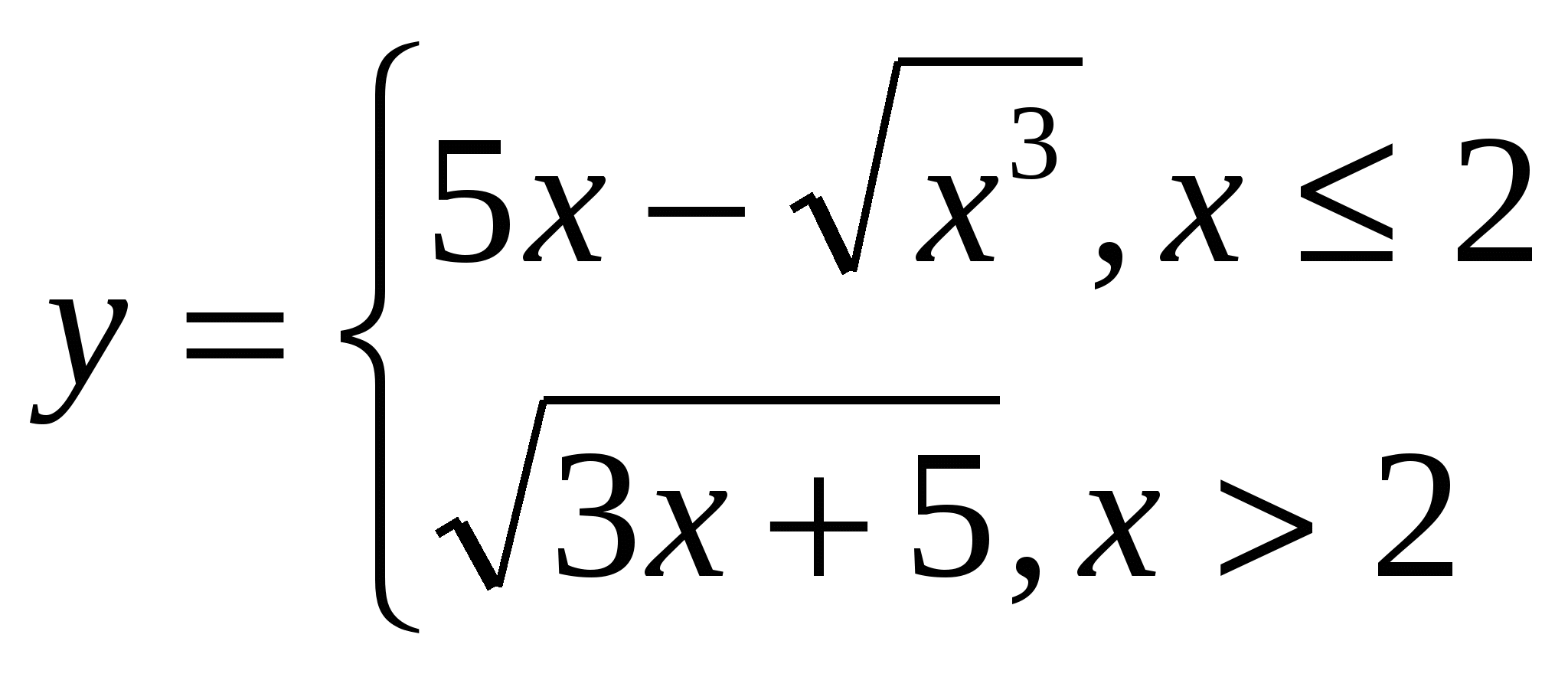 для всех x, принадлежащих отрезку [-7,10], с шагом 1. Записать его в виде блок-схемы. для всех x, принадлежащих отрезку [-7,10], с шагом 1. Записать его в виде блок-схемы.Вариант 8. Составить алгоритм вычисления значений функции Вариант 9. Составить алгоритм вычисления значений функции Вариант 10. Составить алгоритм вычисления значений функции Коды проверяемых профессиональных и общих компетенций при выполнении данного контрольного задания: ПК 1.1. Выполнять разработку спецификаций отдельных компонент. ПК 1.2. Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля. ОК1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес; ОК2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество; ОК3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность; ОК4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития; ОК8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. Теоретические сведения Алгоритмизация задачи — процесс разработки (проектирования) алгоритма для решения задачи с помощью ЭВМ. На этапе постановки задачи описываются исходные данные и предпосылки, формируются правила начала и окончания решения задачи (достижения цели), т. е. разрабатывается информационная или эквивалентная ей математическая модель. Алгоритмов построения моделей не существует. Методом проб и ошибок ведется поиск метода решения задачи. На основании этого метода разрабатывается исходный алгоритм, реализация которого принципиально возможна с помощью ЭВМ. При разработке исходного алгоритма и даже при выборе модели пользователь, решающий конкретную задачу, должен иметь представление о математическом обеспечении ВС или ЭВМ. Алгоритм — понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение указанной цели или на решение поставленной задачи. Таким образом, изучающиеся в школе правила сложения, вычитания, деления, умножения чисел, правила преобразования алгебраических выражений, правила построения геометрических фигур, грамматические правила правописания слов и предложений — все это алгоритмы. Многие правила, инструкции, записанные в воинских уставах, функциональных, должностных обязанностях, представляют собой подробнейшие указания, годные во всевозможных ситуациях. Еще одна причина для изучения алгоритмов заключается в том, что этот процесс развивает у учащихся умение аналитически мыслить. В конце концов, алгоритмы можно рассматривать как особый подход к решению задач, когда важны не столько сами ответы, сколько точные инструкции для их получения. Следовательно, специальные методы проектирования алгоритмов можно считать стратегическим планом решения задачи, который пригодится в любом случае, независимо от того, используется компьютер или нет. Само собой разумеется, что круг задач, которые могут быть решены с помощью какого-либо алгоритма, по существу зависит от точности алгоритмического мышления. Например, невозможно сформулировать алгоритм, который позволит прожить счастливую жизнь или стать богатым и знаменитым. Свойства алгоритма. - Дискретность – выполнение алгоритма разбивается на последовательность законченных шагов, каждое действие должно быть закончено прежде, чем наступит следующее действие. - Понятность – Алгоритм должен быть понятен исполнителю. -Определенность (точность) — будучи понятным, алгоритм не должен содержать предписаний, смысл которых может пониматься неоднозначно, т.е. алгоритм должен исключить произвольное толкование как каждого из предписаний, так и последовательности их выполнения. - Результативность — либо завершение решения задачи после выполнения алгоритма, либо вывод о невозможности продолжения решения по какой-либо из причин, т. е. алгоритм должен oбeспечивать возможность получения результата после конечного числа шагов. - Массовость — единообразное применение алгоритма к любой конкретной формулировке, для решения которой он разработан, т.е. алгоритм должен обеспечивать возможность его применения для решения класса однотипных задач. Команда алгоритма - предписание о выполнении отдельного законченного действия исполнителя. В процессе алгоритмизации задачи исходный алгоритм разбивают на отдельные частные алгоритмы (шаги). Виды алгоритмов: Частные алгоритмы могут быть линейными, разветвляющимися и циклическими. Практически любой сложный алгоритм можно представить в виде комбинации этих трех базовых алгоритмических структур. Линейный алгоритм (последовательность)—последовательность команд (указаний), выполняемых только один раз в порядке их следования. Разветвляющийся алгоритм (альтернатива)- алгоритм, содержащий хотя бы одно условие, в результате проверки которого обеспечивается переход на один из двух возможных шагов. Циклический алгоритм - алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. Оценка корректности алгоритма После представления алгоритма в какой-либо форме, необходимо оценить его корректность. Это означает, что вы должны доказать, что выбранный алгоритм за ограниченный промежуток времени выдает требуемый результат для любых корректных значений входных данных. Например, корректность алгоритма Евклида для вычисления НОД двух чисел, тип, следует из правильности равенства gcd (т, n) = gcd (n, mmod n), которое, в свою очередь, должно быть доказано, а также из простого наблюдения, что второе число на каждой итерации будет все время уменьшаться, и по достижении им нуля, выполнение алгоритма прекращается. Доказать корректность одних алгоритмов очень легко, других — невероятно сложно. Универсальным методом доказательства корректности алгоритма считается метод математической индукции. Дело в том, что алгоритмы по своей природе являются итеративными и описываются в виде последовательности пошаговых инструкций, которые как раз и используются при доказательстве методом индукции. Стоит отметить, что, хотя отслеживание быстродействия алгоритма с помощью нескольких наборов тщательно подобранных входных данных приводит к очень полезным результатам, подобную проверку нельзя считать убедительной при доказательстве корректности алгоритма. Однако доказательством некорректной работы алгоритма может служить лишь один набор входных данных, при обработке которых получается неправильный результат. Если некорректная работа алгоритма будет доказана, придется либо несколько видоизменить его, не выходя за рамки принятых структур данных, методов проектирования и т.п., либо решать проблему более кардинально, пересмотрев принятые ранее принципы и подходы. Анализ алгоритма Обычно создатели алгоритмов стараются, чтобы они удовлетворяли нескольким требованиям. После проверки корректности алгоритма одной из самых важных характеристик является оценка его эффективности. На практике существует два вида оценки эффективности алгоритма: временная и пространственная. Временная эффективность (time efficiency) является индикатором скорости работы алгоритма. Что касается пространственной эффективности (space efficiency), то эта оценка показывает количество дополнительной оперативной памяти, необходимой для работы алгоритма. Еще одной важной характеристикой алгоритма является его простота (simplicity). В отличие от эффективности, которую можно точно определить и оценить с помощью строгих математических выражений, простота алгоритма чем-то напоминает человеческую красоту, понятие которой настолько субъективно, что выработать объективные критерии ее оценки весьма непросто. Например, большинство людей считают, что алгоритм Евклида поиска НОД двух чисел проще, чем тот, которому нас учили в школе, но это вовсе не означает, что он понятнее. В то же время алгоритм Евклида проще алгоритма последовательного перебора целых чисел. Тем не менее простота является важной характеристикой алгоритма, и к ней нужно стремиться. Вы спросите, почему? Дело в том, что простые алгоритмы легче понять и запрограммировать. Следовательно, в полученной программе будет содержаться меньше ошибок. Кроме того, в простоте существует неоспоримая эстетическая привлекательность. Ну и наконец, простые алгоритмы зачастую более эффективны, чем их сложные аналоги. К сожалению, последнее утверждение не всегда выполняется. В подобных случаях необходимо руководствоваться здравым смыслом и принимать компромиссные решения. Следующей важной характеристикой алгоритма является его общность, или универсальность (generality). По сути, здесь можно выделить два момента: общность задачи, для решения которой разработан алгоритм, и диапазон допустимых значений его входных данных. По поводу первого замечания следует сказать, что иногда легче разработать алгоритм для решения общей задачи, чем заниматься поиском решения ее частного случая. В качестве примера рассмотрим такую задачу: определить, являются ли два целых числа взаимно простыми. Напомним, что два числа считаются взаимно простыми, если у них нет общих делителей, кроме 1. В данном случае легче разработать алгоритм для решения общей задачи вычисления НОД двух целых чисел. Затем, чтобы решить исходную задачу, достаточно подставить заданные числа в функцию gcd и проверить, равно ли ее значение 1. Однако бывают случаи, когда разработка более общего алгоритма нежелательна, затруднена или даже невозможна. Например, излишне выполнять сортировку всего списка, содержащего п чисел, чтобы определить их медиану, поскольку достаточно просто найти значение лг-го наименьшего элемента, где т = \п/2]. Еще один пример: известно, что стандартную формулу для поиска корней квадратного уравнения нельзя обобщить для поиска корней полиномов более высоких степеней. Что касается диапазона допустимых значений входных данных алгоритма, то здесь нужно отметить следующее. При разработке алгоритма нужно учитывать, что диапазон изменения значений входных параметров может колебаться в очень широких пределах и должен естественным образом соответствовать решаемой задаче. Например, неестественно в алгоритме поиска НОД исключать из рассмотрения значения входных параметров, равные 1. С другой стороны, хотя стандартную формулу корней квадратного уравнения можно использовать и в случае комплексных коэффициентов, при принятом уровне обобщения этот случай исключают из рассмотрения, поскольку он должен оговариваться отдельно. Если вас не устраивает эффективность, простота или общность алгоритма, придется снова взять в руки карандаш и перепроектировать алгоритм. И даже если анализ алгоритма привел к положительным результатам, имеет смысл поискать другое алгоритмическое решение задачи. Достаточно вспомнить три алгоритма определения НОД, рассмотренных в предыдущем разделе. Вообще говоря, не стоит надеяться, что вы с первой попытки найдете оптимальное решение задачи. Самое меньшее, что можно сделать, попытаться оптимизировать созданный алгоритм. Всегда помните высказывание Антуана де Сент-Экзюпери (Antoine de Saint-Exupery), известного французского писателя, летчика и авиаконструктора: "Конструктор достигает совершенства не тогда, когда ему больше нечего добавить к своему детищу, а тогда, когда больше ничего удалить". Важные типы задач Среди огромного количества задач, встречающихся в вычислительной технике, можно выделить несколько типов, которым ученые всегда уделяли особое внимание. Подобный интерес вызван либо практическим значением задачи, либо какими-то ценными ее свойствами, представляющими особый интерес для исследования. В этом разделе кратко рассматриваются наиболее важные типы задач:
Сортировка Задача сортировки (sorting problem) заключается в упорядочении заданного списка каких-либо элементов в возрастающем порядке. Само собой разумеется, что для определенности задачи структура этих элементов списка должна позволять их упорядочить. На практике обычно требуется отсортировать по возрастанию список чисел, расположить символы и строки в алфавитном порядке или, что наиболее важно, упорядочить набор записей, содержащих различную информацию, наподобие той, что хранится в папках со сведениями об учащихся школы, в читательских формулярах библиотеки, в отделе кадров о сотрудниках организации. В случае набора записей необходимо выбрать фрагмент записи, содержащий данные, по которым будет осуществляться сортировка. Например, набор записей о студентах можно отсортировать по фамилии, идентификационному номеру или по среднему баллу. Специально отобранный фрагмент данных называется ключом (key). Специалисты по информатике часто говорят о сортировке списка ключей, даже если элементы этого списка являются не записями, а, скажем, целыми числами. Поиск Задача поиска связана с нахождением заданного значения, называемого ключом поиска (search key), среди заданного множества. Существует огромное количество алгоритмов поиска, так что есть из чего выбирать. Их сложность варьируется от самых простых алгоритмов поиска методом последовательного сравнения, до чрезвычайно эффективных, но ограниченных алгоритмов бинарного поиска, а также алгоритмов, основанных на представлении базового множества в иной, более подходящей для выполнения поиска форме. Последние из упомянутых здесь алгоритмов имеют особое практическое значение, поскольку применяются в реально действующих приложениях, выполняющих выборку и хранение массивов информации в огромных базах данных. Для решения задачи поиска также не существует единого алгоритма, который бы наилучшим образом подходил для всех случаев. Некоторые из алгоритмов выполняются быстрее остальных, но для их работы требуется дополнительная оперативная память. Другие выполняются очень быстро, но их можно применять только для предварительно отсортированных массивов, и т.п. В отличие от алгоритмов сортировки в алгоритмах поиска нет проблемы устойчивости, но при их использовании могут возникать другие сложности. В частности, в тех приложениях, где обрабатываемые данные могут часто изменяться, причем количество изменений сравнимо с количеством операций поиска, поиск следует рассматривать в неразрывной связи с двумя другими операциями — добавления элемента в набор данных и удаления из него. В подобных ситуациях необходимо видоизменить структуры данных и алгоритмы так, чтобы достигалось равновесие между требованиями, выдвигаемыми к каждой операции. Кроме того, организация очень больших наборов данных с целью выполнения в них эффективного поиска (а также добавления и удаления элементов) представляет собой чрезвычайно сложную задачу, решение которой особенно важно с точки зрения практического применения. Обработка строк В связи с быстрым увеличением в последнее время количества приложений, связанных с обработкой нечисловых данных, интерес ученых и специалистов-практиков все больше привлекают алгоритмы обработки строк. Строкой (string) называется последовательность символов, взятых из заранее определенного алфавита. Практический интерес представляют, например, текстовые строки, состоящие из букв, цифр и специальных символов; битовые строки, состоящие из нулей и единиц; последовательности генов, которые могут быть смоделированы с помощью строк символов, взятых из четырехсимвольного алфавита {А, С, G, Т}. Тем не менее стоит отметить, что алгоритмы обработки строк стали важны для вычислительной техники очень давно — с тех пор, как появились первые языки программирования и соответствующие им программы — компиляторы. Существует одна специфическая задача, которая привлекла особое внимание специалистов по информатике. Речь идет о поиске заданного слова в строке текста. Ее назвали поиском подстрок (string matching). Для выполнения такого специфического поиска разработано несколько алгоритмов. Задачи из теории графов Одной из самых старых и, пожалуй, наиболее интересных областей алгоритмики является обработка графов. Нестрого граф можно определить как набор точек, называемых вершинами, часть из которых соединена отрезками, называемыми ребрами. (Более строгое определение графа будет дано в следующем разделе.) Графы являются довольно интересным объектом для изучения как с теоретической, так и с практической точек зрения. С помощью графов можно смоделировать довольно большое количество процессов, происходящих в реальной жизни, например функционирование транспортных и коммуникационных сетей, календарное планирование проекта и т.д. Одна из последних интересных задач — оценка "диаметра" Web, заключающаяся в определении максимального количества ссылок, которые нужно пройти от одной Web-страницы до другой по оптимальному маршруту. К числу основных алгоритмов теории графов относят следующие:
Вопросы по ОП.08 Теория алгоритмов
ЛИТЕРАТУРА: Основная:
Дополнительная:
1 2 |
