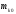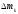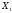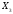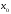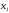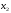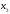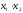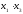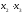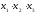Корреляционный анализ
 Скачать 212.5 Kb. Скачать 212.5 Kb.
|
|
2.2 Определение центра плана (основной уровень) и уровня варьирования факторов Находим центр плана: 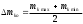 . .Находим полуразмах: 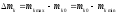 . .Рассчитываем и оформляем в виде таблицы. 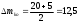 , , 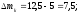 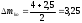 , , 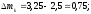 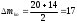 , , 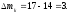 Таблица 3 – Центр плана и полуразмах
Рассчитываем нижний уровень варьирования факторов: 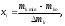 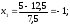 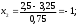 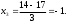 Рассчитываем верхний уровень варьирования факторов:  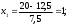 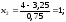 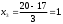 2.3 Построение матрицы планирования Так как мы имеем 2 уровня варьирования факторов и 3 фактора, то получаем матрицу 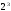 . Число опытов равно 8. . Число опытов равно 8.Таблица 3 – Матрица планирования типа 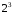
Составляем расширенную матрицу планирования для того, чтобы учесть взаимодействие факторов. Таблица 4 – Расширенная матрица планирования
2.4 Проверка однородности дисперсии и равноточности измерения в разных сериях Для проверки однородности дисперсии был выбран критерий Кохрена. Для этого рассчитываем дисперсию в каждом опыте по формуле: 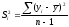 . .Находим: 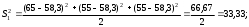 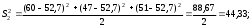 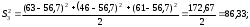 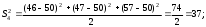 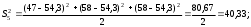 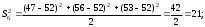 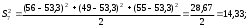 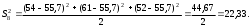 Условия проверки однородности дисперсий по критерию Кохрена: 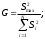 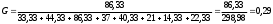 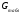 для уровня значимости 0,05 равна 0,32. для уровня значимости 0,05 равна 0,32.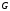 < <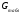 , следовательно, дисперсия однородна и измерения в разных сериях равноточны. , следовательно, дисперсия однородна и измерения в разных сериях равноточны.2.5 Коэффициенты уравнения регрессии Находим коэффициенты уравнения регрессии. 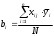 . .Находим: 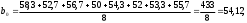 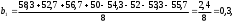 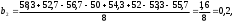 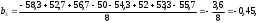 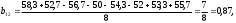 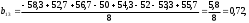 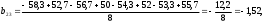 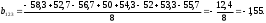 Следовательно, уравнение регрессии примет вид: 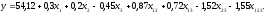 2.6 Дисперсия воспроизводимости Вычисляем значение дисперсии воспроизводимости по формуле: 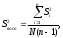 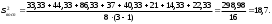 2.7 Проверка значимости коэффициентов уравнения регрессии Проверяем значимость коэффициентов уравнения регрессии по критерию Стьюдента: 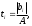 где где 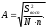 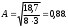 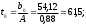 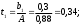 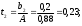 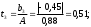 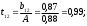 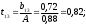 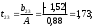 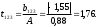 Условие значимости 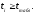 Для уровня значимости α = 0,05 и числа степеней свободы f = N - 1 =8 - 1 = 7 находим табличное значение критерия Стьюдента Для уровня значимости α = 0,05 и числа степеней свободы f = N - 1 =8 - 1 = 7 находим табличное значение критерия Стьюдента 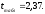 Сравниваем расчетное значение с табличным и видим, что значение 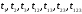 незначительные и их коэффициенты следует исключить из уравнения регрессии. Так как коэффициенты получились незначимы и мы не имеем возможности заново поставить новый эксперимент и продолжаем вычисления, выбрав наиболее близкие к значимым коэффициенты. незначительные и их коэффициенты следует исключить из уравнения регрессии. Так как коэффициенты получились незначимы и мы не имеем возможности заново поставить новый эксперимент и продолжаем вычисления, выбрав наиболее близкие к значимым коэффициенты.Уравнение регрессии примет вид: 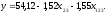 2.8 Проверка адекватности уравнения регрессии Для проверки используется критерий Фишера: 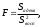 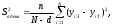 где d – количество коэффициентов уравнения регрессии. Находим значения 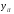 : :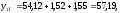 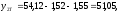 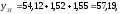 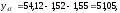 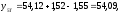 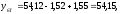 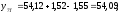 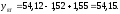 Найдем значение 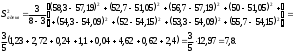 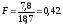 Находим табличное значение критерия Фишера для степеней свободы 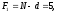 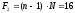 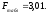 Сравниваем условие 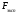 < <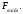 , значит, модель адекватна. , значит, модель адекватна.Выводы: Уравнение регрессии имеет вид: 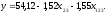 Анализ значимости коэффициентов уравнении регрессии показал, что влияние всех факторов незначимо. Модель адекватна, так как критерий адекватности меньше табличного. Измерения в различных серий равноточны. ЗАКЛЮЧЕНИЕ Термин «корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальтоном в 1886 году. Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон. Задачи с одним выходным параметром имеют очевидные преимущества. Но на практике чаще всего приходится учитывать несколько выходных параметров. Иногда их число довольно велико. Так, например, при производстве резиновых и пластмассовых изделий приходится учитывать физико-механические, технологические, экономические, художественно-эстетические и другие параметры (прочность, эластичность, относительное удлинение и т.д.). Математические модели можно построить для каждого из параметров, но одновременно оптимизировать несколько функций невозможно. Обычно оптимизируется одна функция, наиболее важная с точки зрения цели исследования, при ограничениях, налагаемых другими функциями. Поэтому из многих выходных параметров выбирается один в качестве параметра оптимизации, а остальные служат ограничениями. Всегда полезно исследовать возможность уменьшения числа выходных параметров. Для этого и используется корреляционный анализ. С использованием результатов корреляционного анализа исследователь может делать определённые выводы о наличии и характере взаимозависимости, что уже само по себе может представлять существенную информацию об исследуемом объекте. Результаты могут подсказать и направление дальнейших исследований, и совокупность требуемых методов, в том числе статистических, необходимых для более полного изучения объекта[7]. Особенно реальную пользу применение аппарата корреляционного анализа может принести на стадии ранних исследований в областях, где характеры причин определённых явлений ещё недостаточно понятны. Это может касаться изучения очень сложных систем различного характера: как технических, так и социальных. СПИСОК ЛИТЕРАТУРЫ Сидоренко Е.В. Методы математической обработки в психологии. Спб.: ООО «Речь», 2000. – 350 с. Лекция на тему: "Корреляционный анализ''// www.kgafk.ru, 2006, 8 с. Ковалев В.В, Волкова О.Н., Анализ хозяйственной деятельности предприятия// polbu.ru, 2005, 2 с. Поляков Л.Е., Коэффициент ранговой корреляции Спирмена// www.eduhmao.ru, 1971, 2 с. Бондарь А.Г., Статюха Г.А. Планирование эксперимента в химической технологии. Киев: Высшая школа, 1976 – 335 с. Адлер Ю.П., Грановский Ю.В., Маркова Е.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976.–278 с. Андерсон Т., Введение в многомерный статистический анализ// www.ami.nstu.ru, 1963, 24 с. |