ТЕОРИЯ ПЛАНИРОВАНИЯ. Составление матрицы планирования пфэ 2

• Название: Составление матрицы планирования пфэ 2
• Дата: 21.07.2021
• Размер: 145.62 Kb.
• Имя файла: ТЕОРИЯ ПЛАНИРОВАНИЯ.docx
• Тип: Документы; #224993

Оглавление:

Составление матрицы планирования ПФЭ 2² 2

Проверка свойств планов-матриц ПФЭ 2^k и ДФЭ 2^k-p 11

Список литературы: 12

Составление матрицы планирования ПФЭ 2²

Полным факторным экспериментом называется такой эксперимент, при котором определяется значение выходного параметра или параметра оптимизации Y при всех возможных сочетаниях уровней варьирования факторов.

В эксперимент включают х₁, х₃, …, х_k т.е. k – факторов, для каждого из которых следует установить q уровней.

Для осуществления ПФЭ нужно поставить N = q^k опытов. Наиболее распространены эксперименты, у которых факторы варьируют на двух уровнях – верхнем и нижнем, т.е. q = 2. Это эксперименты типа 2^k.

Планирование, проведение и обработка результатов ПФЭ включают следующие этапы:

• 
  кодирование факторов;
  
• 
  составление плана эксперимента или плана-матрицы;
  
• 
  рандомизацию опытов;
  
• 
  реализацию плана эксперимента;
  
• 
  проверку воспроизводимости опытов;
  
• 
  вычисление и проверку значимости коэффициентов регрессии;
  
• 
  проверку адекватности регрессионной модели.
  

Поскольку факторы процесса неоднородны и имеют различные единицы измерения, а числа, выражающие величины факторов, имеют различные порядки, их следует привести к единой системе счисления путем перехода от действительных значений факторов к кодированным по формулам: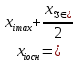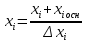





D ,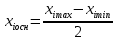
Где

• 
  х_iосн – основной уровень фактора;
  
• 
  X_i – кодированное значение фактора;
  
• 
  х_imax– верхний уровень фактора;
  
• 
  х_imin – нижний уровень фактора;
  
• 
  D х_i - интервал варьирования фактора;
  
• 
  i – номер фактора.
  

Вводят условное обозначение верхнего, нижнего и основного уровней фактора соответственно +1, -1, 0. При построении планов-матриц планирования эксперимента цифры (единицы) можно опускать и писать только их знаки «+» или «-».

Затем строят план-матрицу эксперимента. Построение плана-матрицы сводится к стандартной форме записи условий проведения экспериментов в виде таблицы, в строках которой записывают данные опытов, в столбцах – факторы (в кодах «+» и «-») с реализацией всех возможных сочетаний комбинаций факторов.

В первом столбце таблицы следует менять знаки поочередно, во втором столбце – чередовать их через два, в третьем – через четыре, в четвертом – через восемь и т.д., т.е. по степеням двойки. Общее количество строк в матрице плана для реализации всех возможных сочетаний уровней факторов определяют по формуле N = 2^k.

Пользуясь результатами факторного эксперимента, можно получить описание изучаемой системы или процесса в виде полиномиального уравнения линейной регрессии Y=b₀+b₁X₁+b₂X₂+…+b_kX_k, где выборочные коэффициенты параметров модели процесса b₀, b₁, b₂ и т.д. являются статистическими оценками теоретических коэффициентов  и т.д., а Y – оценка математического ожидания выходного параметра или параметра оптимизации процесса. Можно также получить описание изучаемого процесса в виде полиномиальных уравнений, содержащих эффекты взаимодействия факторов, а также квадратичные члены.

Первый этап планирования эксперимента для получения линейной модели основан на варьировании факторов на двух уровнях. В случае если число факторов известно, можно сразу найти число опытов, необходимое для реализации всех возможных сочетаний уровней факторов.

Формула, которая для этого используется: N=2^k. Где N — число опытов; к — число факторов; 2 — число уровней. В нашем случае к=2.

Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.

Если число уровней каждого фактора равно двум, то имеем полный факторный эксперимент типа 2^к, где цифра 2 указывает на число уровней факторов в планируемом эксперименте.

Нетрудно написать все сочетания уровней в эксперименте с двумя факторами. Напомним, что в планировании эксперимента используются кодированные значения факторов: +1 и -1 (часто для простоты записи единицы опускают). Условия эксперимента записывают в виде таблицы где строки соответствуют различным опытам, а столбцы — значениям факторов и параметров оптимизации. Такая таблица называется матрицей планирования эксперимента.

Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку — вектор-строкой. Таким образом, имеем два вектор-столбца независимых переменных и один вектор-столбец параметра оптимизации.

Матрица планирования для двух факторов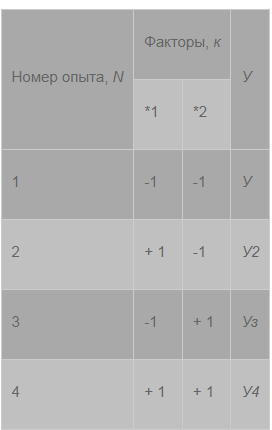



Если для двух факторов все возможные комбинации уровней легко найти прямым перебором, то с ростом числа факторов возникает необходимость в применении существующих приемов построения матриц.

Чаще других используется три приема, основанных на переходе от матриц меньшей размерности к матрицам большей размерности.

Первый прием основан на правиле чередования знаков. В первом столбце знаки меняются поочередно, во втором столбце они чередуются через 2, в третьем — через 4, в четвертом — через 8 и т.д.

Второй прием. При добавлении нового фактора каждая комбинация уровней исходного плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. То есть сначала надо записать все опыты плана для одного уровня нового фактора, допустим, верхнего (+1), а затем повторить его для нижнего уровня (-1). Эффекты х_ь х₂, и х₃ называются линейными эффектами. Вот как это выглядит при переходе от эксперимента 2² к г. Этот прием распространяется на построение матриц любой размерности.


Третий прием основан на правиле перемножения столбцов матрицы. При построчном перемножении двух столбцов матрицы произведение единиц с одноименными знаками дает +1, а с разноименными -1. Воспользовавшись этим правилом, получим для случая, который мы рассматриваем, вектор-столбцы произведений х_{х₂, х₂х₃ и Xj х₃ 

Эффект взаимодействия двух факторов называется эффектом взаимодействия первого порядка.


План полного трехфакторного эксперимента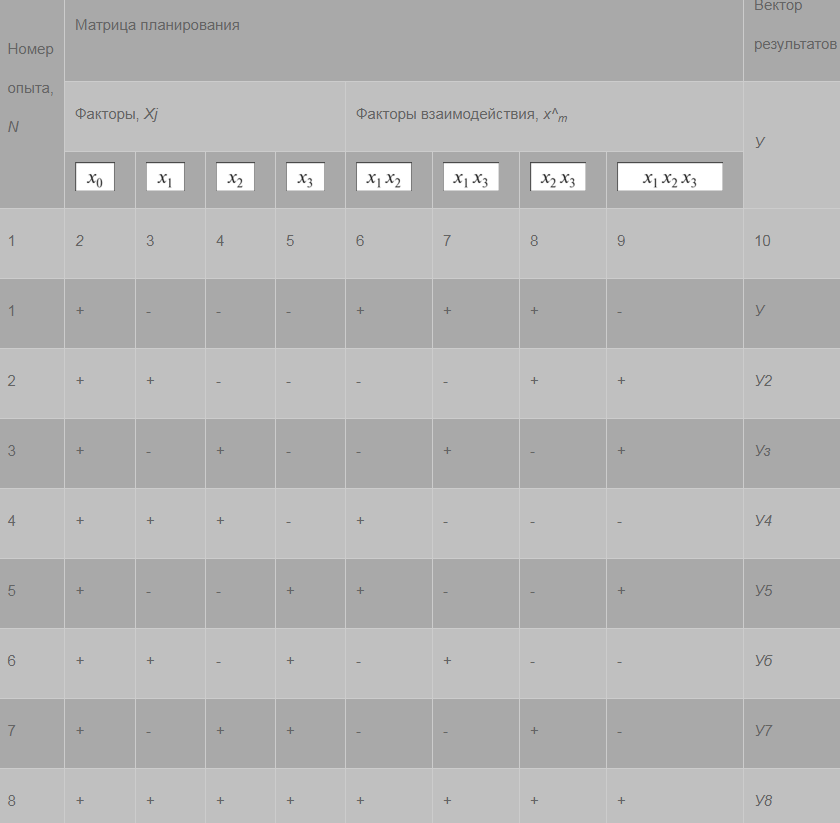



Далее повторим еще раз перемножение знаков уже трех факторов и получим эффект взаимодействия трех факторов, вектор-столбец х,х₂*з которого называется эффектом взаимодействия второго порядка.

Нулевой уровень х₀ вводится для удобства дальнейших расчетов.

Вообще, эффект взаимодействия максимального порядка в ПФЭ имеет порядок, на единицу меньший числа факторов.

Число всех возможных эффектов (включая х₀, линейные и эффекты взаимодействия всех порядков) равно числу опытов полного факторного эксперимента.

Чтобы найти число возможных взаимодействий (С*) некоторого порядка, можно воспользоваться обычной формулой числа сочетаний:


г 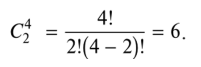де к — число факторов; п — число элементов во взаимодействии. Так, для плана 2³ число взаимодействий первого порядка равно трем, а для плана 2⁴ — шести:

Физический смысл эффекта взаимодействия заключается в следующем: например, пусть на процесс дублирования деталей одежды влияют два фактора: температура и время дублирования. В области низких температур увеличение времени повышает прочность клеевого соединения. При переходе в область высоких температур эта закономерность нарушается. Здесь, напротив, необходимо уменьшать время дублирования, чтобы получить высокую прочность клеевого соединения. Это и есть проявление эффекта взаимодействия.

Зависимость количества взаимодействий различного порядка от числа факторовПФЭ. Полное число всех возможных эффектов, включая их₀, равно числу опытов ПФЭ.

Взаимосвязь характеристик ПФЭ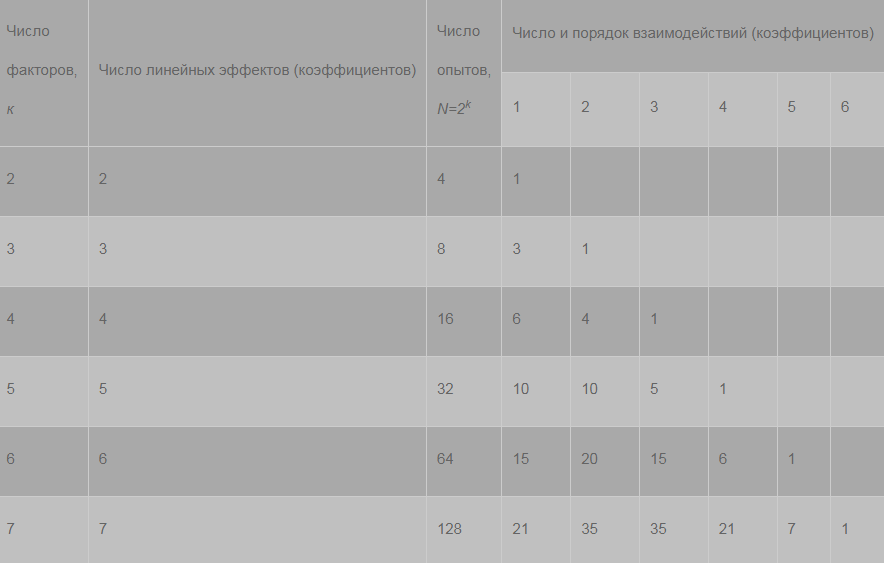



Геометрической интерпретацией полного факторного эксперимента 2³ служит куб, координаты вершин которого задают условия опытов.

Если поместить центр куба в точку основного уровня факторов, а масштабы по осям выбрать так, чтобы интервал варьирования равнялся единице, то получится куб.

К 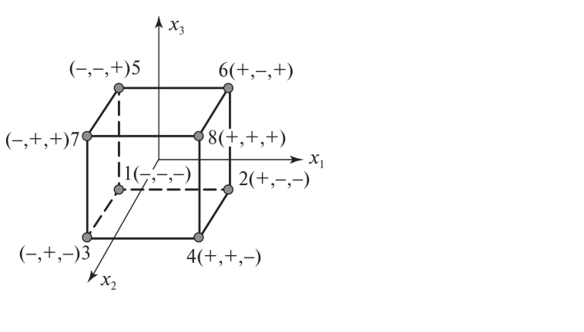уб задает область эксперимента, а центр куба является центром плана ПФЭ.

Если к > 3, то фигура, задающая в пространстве область определения параметра оптимизации, называется гиперкубом

Проверка свойств планов-матриц ПФЭ 2^k и ДФЭ 2^k-p

После построения плана матрицы ПФЭ 2^k и ДФЭ 2^k-p необходимо проверить ее свойства.

Симметричность относительно центра эксперимента: алгебраическая сумма элементов столбца каждого фактора, кроме столбца, отвечающего свободному члену b₀, должна быть равна нулю, т.е.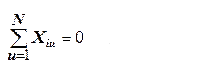



где u – номер строчки плана-матрицы;

i – номер фактора;

N – общее число строчек плана-матрицы.

Нормировка: сумма квадратов элементов каждого столбца должна быть равна числу строчек плана-матрицы, т.е.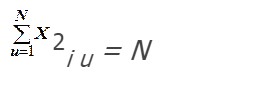



 Ортогональность: сумма построчных произведений любых двух столбцов плана-матрицы должна быть равна нулю, т.е.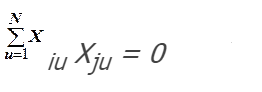



где X_iu X_ju- комбинация факторов в u-й строчке, i ≠ j.

Если план-матрица отвечает вышеперечисленным свойствам, то она соответствует и свойству ротатабельности.

Список литературы:

1.Рогов, В. А. Методика и практика технических экспериментов : учебное пособие для вузов / В. А. Рогов, Г. Г. Позняк. – М. : Академия, 2005. – 283 с.

2. Современный эксперимент : подготовка, проведение, анализ результатов : учебник для вузов / В. Г. Блохин, О. П. Глудких, А. И. Гуров, Н. А. Ханин ; под ред. О. П. Глудких. – М. : Радио и связь, 1997.