Корреляционный анализ
 Скачать 212.5 Kb.
|
|
Рассчитываем эмпирическую величину коэффициента корреляции по формуле расчета коэффициента корреляции Браве–Пирсона:  Определяем критические значения для полученного коэффициента корреляции по таблице. При нахождении критических значений для вычисленного коэффициента линейной корреляции Пирсона число степеней свободы рассчитывается как f = n – 2 = 8. rкрит=0,72 > 0,54 , следовательно, гипотеза Н1 отвергается и принимается гипотеза H0, иными словами, связь между временем решения наглядно-образных и вербальных заданий теста не доказана[1]. Коэффициент ранговой корреляции Спирмена Если потребуется установить связь между двумя признаками, значения которых в генеральной совокупности распределены не по нормальному закону, т. е. предположение о том, что двумерная выборка (xi и yi) получена из двумерной нормальной генеральной совокупности, не принимается, то можно воспользоваться коэффициентом ранговой корреляции Спирмена (  ): 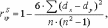где dx и dy – ранги показателей xi и yi; n – число коррелируемых пар. Коэффициент ранговой корреляции также имеет пределы 1 и –1. Если ранги одинаковы для всех значений xi и yi, то все разности рангов (dx - dy) = 0 и = 1. Если ранги xi и yi расположены в обратном порядке, то = -1. Таким образом, коэффициент ранговой корреляции является мерой совпадения рангов значений xi и yi. Когда ранги всех значений xi и yi строго совпадают или расположены в обратном порядке, между случайными величинами Х и Y существует функциональная зависимость, причем эта зависимость не обязательно линейная, как в случае с коэффициентом линейной корреляции Браве-Пирсона, а может быть любой монотонной зависимостью (т. е. постоянно возрастающей или постоянно убывающей зависимостью). Если зависимость монотонно возрастающая, то ранги значений xi и yi совпадают и = 1; если зависимость монотонно убывающая, то ранги обратны и = –1. Следовательно, коэффициент ранговой корреляции является мерой любой монотонной зависимости между случайными величинами Х и Y.Из формулы видно, что для вычисления необходимо сначала проставить ранги (dx и dy) показателей xi и yi, найти разности рангов (dx - dy) для каждой пары показателей и квадраты этих разностей (dx - dy)2. Зная эти значения, находятся суммы  , учитывая, что 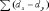 всегда равна нулю. Затем, вычислив значение , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным. Если 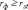 , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если 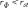 , то между признаками наблюдается недостоверная корреляционная взаимосвязь.Коэффициент ранговой корреляции Спирмена вычисляется значительно проще, чем коэффициент корреляции Браве-Пирсона при одних и тех же исходных данных, поскольку при вычислении используются ранги, представляющие собой обычно целые числа. Коэффициент ранговой корреляции целесообразно использовать в следующих случаях: - если экспериментальные данные представляют собой точно измеренные значения признаков Х и Y и требуется быстро найти приближенную оценку коэффициента корреляции. Тогда даже в случае двумерного нормального распределения генеральной совокупности можно воспользоваться коэффициентом ранговой корреляции вместо точного коэффициента корреляции Браве-Пирсона. Вычисления будут существенно проще, а точность оценки генерального параметра р с помощью коэффициента при больших объемах выборки составляет 91,2% по отношению к точности оценки по коэффициенту корреляций; - когда значения xi и (или) yi заданы в порядковой шкале (например, оценки судей в баллах, места на соревнованиях, количественные градации качественных признаков), т. е. когда признаки не могут быть точно измерены, но их наблюдаемые значения могут быть расставлены в определенном порядке. Пример 2. Определить достоверность взаимосвязи между показателями веса и максимального количества сгибания и разгибания рук в упоре лежа у 10 исследуемых с помощью расчета рангового коэффициента корреляции, если данные выборок таковы: xi,кг55; 45; 43; 47; 47; 51; 48; 60; 53;50 yi, кол-во раз 26; 20; 25; 22; 27; 28; 16; 15; 18; 24 Решение 1. Расчет рангового коэффициента корреляции Спирмена произведем по формуле: 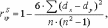где: dx и dy — ранги показателей х и у; n — число коррелируемых пар или исследуемых. 2 Данные тестирования занести в рабочую таблицу и сделать необходимые расчеты. Таблица 2 – Данные тестирования
Тогда 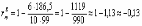 3. Сравнить расчетное значение рангового коэффициента корреляции(rф =-0,13) с табличным значением для n = 10 при α = 5% и сделать вывод. Вывод: 1) т.к. rф = -0,13 < 0, то между данными выборок наблюдается прямая отрицательная взаимосвязь, т.е. увеличением показателей веса вызывает снижение максимального количество сгибаний и разгибаний рук в упоре лежа в группе исследуемых; 2) т.к. rф = -0,13 < rst = 0,64 для n = 10 при α = 5%, то с уверенностью Р = 95% можно говорить о том, что выявленная зависимость недостоверна. Основные свойства коэффициентов корреляции К основным свойствам коэффициента корреляции необходимо отнести следующие: - коэффициенты корреляции способны характеризовать только линейные связи, т.е. такие, которые выражаются уравнением линейной функции. При наличии нелинейной зависимости между варьирующими признаками следует использовать другие показатели связи; - значения коэффициентов корреляции – это отвлеченные числа, лежащее в пределах от —1 до +1, т.е. -1 < r < 1; - при независимом варьировании признаков, когда связь между ними отсутствует, r= 0; - при положительной, или прямой, связи, когда с увеличением значений одного признака возрастают значения другого, коэффициент корреляции приобретает положительный знак и находится в пределах от 0 до +1, т.е. 0 < r < 1; - при отрицательной, или обратной, связи, когда с увеличением значений одного признака соответственно уменьшаются значения другого, коэффициент корреляции сопровождается отрицательным знаком и находится в пределах от 0 до –1, т.е. -1 < r <0; - чем сильнее связь между признаками, тем ближе величина коэффициента корреляции к 1. Если r = ±1, то корреляционная связь переходит в функциональную, т.е. каждому значению признака Х будет соответствовать одно или несколько строго определенных значений признака Y; - только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Этот параметр зависит от числа степеней свободы f= n –2, где n – число коррелируемых пар показателей Х и Y. Чем больше n, тем выше достоверность связи при одном и том же значении коэффициента корреляции. [2] Проверка значимости коэффициентов корреляции Для проверки значимости коэффициентов корреляции чаще всего используют распределение Стьюдента и условие: 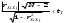 , f = N – 2, α = 0,05.Если условие выполняется, то гипотеза об отсутствии корреляционной связи принимается[5]. Критические значения коэффициента парной корреляции Таблица 3 - Критические значения коэффициента парной корреляции при α=0,05
 Для проверки значимости коэффициента парной корреляции нужно сравнить его значение с табличным (критическим) значением r, которое приведено в таблице 3. Для пользования этой таблицей нужно знать число степеней свободы f = N – 2 и выбрать определенный уровень значимости, например равный 0,05. Такое значение уровня значимости называют еще 5%-ным уровнем риска, что соответствует вероятности верного ответа при проверке нашей гипотезы Р = 1 – α = 0,95, или 95%. Это значит, что в среднем только в 5% случаев возможна ошибка при проверке гипотезы.В практических исследованиях 5%-ный уровень риска применяется наиболее часто. Но экспериментатор всегда свободен в выборе уровня значимости, и возможны ситуации, в которых, например, требуется 1%-ный уровень риска. При этом возрастает надежность ответа. Проверка гипотезы сводится к сравнению абсолютной величины коэффициента парной корреляции с критическим значением. Если экспериментально найденное значение r меньше критического, то нет оснований считать, что имеется тесная линейная связь между параметрами, а если больше или равно, то гипотеза о корреляционной линейной связи не отвергается[6]. 2. РЕШЕНИЕ ЗАДАЧИ 2.1 Условие задачи Рассчитать полным факторным экспериментом влияние давления 5-20 МПа, жирности 4-2,5м.д. и кислотности 14-20°Т на качество продукции. Таблица 1 – Условие задачи
Таблица 2 – Функция отклика
|
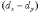
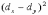
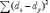= 186,5
