Кр13. 04. 02. Эсм117. 2018. Пз оптимизация развития электроэнергетических систем
 Скачать 256.47 Kb. Скачать 256.47 Kb.
|
«Оптимальное распределение нагрузки между генераторами электростанции»Суммарная мощность генераторов ЭЭС, как правило, превышает суммарную потребляемую мощность. Поэтому в рабочий режим включаются не все агрегаты, а какая-то их большая часть. Одним из основных требований, предъявляемых к ЭЭС, является экономичность ее режима работы, отвечающего минимальным затратам на единицу выработанной электроэнергии. В связи с этим возникает оптимизационная задача экономичного распределения активной мощности между отдельными агрегатами электростанции и между электростанциями в ЭЭС. В качестве критерия оптимальности принимается минимум суммарного расхода топлива при выполнении баланса мощности. Для каждого отдельного агрегата существует так называемая расходная характеристика В(Рг), определяющая зависимость расхода топлива В от мощности, выдаваемой генератором Рг. Минимум функции ищется при условии выполнения баланса активной мощности для станции. Это условие запишем в виде 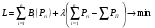 , (3.1) , (3.1)где λ-неопределенный множитель Лагранжа Для целевой функции и баланса активной мощности запишем функцию Лагранжа и вместо условного минимума целевой функции будем искать безусловный минимум функции Лагранжа. Для целевой функции и баланса активной мощности запишем функцию Лагранжа и вместо условного минимума целевой функции будем искать безусловный минимум функции Лагранжа. 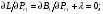 (3.2) (3.2)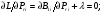 (3.3) (3.3)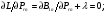 (3.4) (3.4)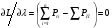 (3.5) (3.5)Из уравнений видно, что искомому решению соответствует условие равенства между собой частных производных Эти частные производные называются относительными приростами расхода топлива и обозначаются (i=1, 2, ...n). Таким образом, оптимальное распределение активной мощности между агрегатами одной станции будет при равенстве относительных приростов расхода топлива отдельных агрегатов станции. Обычно при решении задачи оптимального распределения активных мощностей используются характеристики относительных приростов (Pгi)- получаемые дифференцированием расходных характеристик. 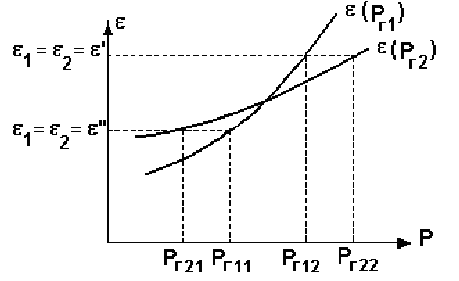 Рисунок 3.1 Распределение активной мощности между двумя агрегатами Принцип равенства относительных приростов расхода топлива при оптимизации распределения активной мощности между двумя агрегатами станции иллюстрируется рис.3.1. При распределении мощности ∑РП1 между двумя агрегатами первый агрегат нужно загрузить мощностью –Pг11, а второй - мощностью Рг21. При этом ∑РП1=РП11+РП21, а относительные приросты расхода топлива ε1=ε2=ε'. При распределении мощности ∑РП2 между двумя агрегатами первый агрегат нужно загрузить мощностью Рг12, а второй - мощностью Рг22. При этом ∑РП2=Рг12+РГ22, а относительные приросты расхода топлива ε1=ε2=ε''. Видно, что до точки пересечения характеристик большую нагрузку следует давать на первый агрегат, а после точки пересечения - на второй. Принцип равенства относительных приростов расхода топлива может быть распространен с определенными дополнениями на задачу оптимального распределения активной мощности между отдельными электростанциями ЭЭС. Электростанции в ЭЭС объединены на параллельную работу электрическими сетями. Экономичность режима работы ЭЭС определяется не только суммарным расходом топлива, но и потерями мощности в электрических сетях. Потерн активной мощности в сетях зависят от перетоков по ним мощностей, связанных с распределением суммарной нагрузки между отдельными электростанциями. Чем длиннее и загруженнее линии связи между отдельными станциями, тем сильнее влияние потерь мощности в сетях на экономичный режим работы ЭЭС и тем ощутимее поправки к распределению мощностей между станциями, выполненному по условию равенства относительных приростов расхода топлива. Таким образом, вопрос об экономичном распределении активной мощности между станциями ЭЭС следует решать с учетом ряда дополнительных условий, характеризующих работу конкретной ЭЭС. Задание: Рн=1150 МВт МВт 450 МВт 450 МВт 450 МВт Рисунок 3.2. Заданные мощности агрегатов и нагрузки Исходные данные: Мощность одного генератора : РГ=450 МВт Мощность нагрузки: РН=1150 МВт   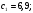 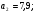 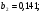 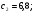 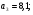 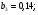 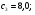 Выражения для определения расходных характеристик: 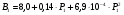 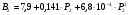 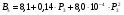 Экв.агр. 1-2 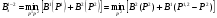 Зададимся точками эквивалентных оптимальных расходных характеристик для генераторов 1,2: Р1,2= 760 ,770,780,790,800,810,820,830,840 МВт Таблица 3.1 Оптимальные расходные характеристики для Р1,2=760 МВт
Таблица 3.2 Оптимальные расходные характеристики для Р1,2=770 МВт
Таблица 3.3 Оптимальные расходные характеристики для Р1,2=780 МВт
Таблица 3.4 Оптимальные расходные характеристики для Р1,2=790 МВт
Таблица 3.5 Оптимальные расходные характеристики для Р1,2=800 МВт
Таблица 3.6 Оптимальные расходные характеристики для Р1,2=810 МВт
Таблица 3.7 Оптимальные расходные характеристики для Р1,2=820 МВт
Таблица 3.8 Оптимальные расходные характеристики для Р1,2=830 МВт
Таблица 3.9 Оптимальные расходные характеристики для Р1,2=840 МВт
Результаты расчетов таблиц 3.1-3.9 занесем в Таблицу 3.10 Таблица 3.10 Оптимальные расходные характеристики для Р1,2
Рассчитаем оптимальную эквивалентную расчетную характеристику для всех трёх генераторов станции. 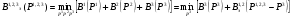 Таблица 3.11 Оптимальные расходные характеристики для Р1,2,3
Вывод: Из последней таблицы видно , что наиболее оптимальные нагрузки генераторов : P1=400 МВт ; Р2= 410 МВт ; Р3=340 МВт. ЗаключениеОптимизация режимов работы электроэнергетической системы (ЭЭС) сложная многоуровневая задача. К ее решению необходимо подходить комплексно на всех иерархических уровнях ЭЭС. Оптимальный режим энергосистемы – это такой режим из допустимых, т.е. удовлетворяющих условиям надежности и качества электроэнергии, при котором обеспечивается минимум затрат при заданной в каждый момент времени нагрузке потребителей. Оптимальное управление режимами достигается различными способами:
В курсовом проекте рассмотрены основные задачи ,решаемые при оптимизации режима:
Список использованной литературы
|
