Кр13. 04. 02. Эсм117. 2018. Пз оптимизация развития электроэнергетических систем
 Скачать 256.47 Kb. Скачать 256.47 Kb.
|
|
Изм. Лист № докум. Подпись Дата Лист 5 КР-13.04.02.ЭСм-1-17.2018.ПЗ Оптимизация развития электроэнергетических систем Лит. Листов 23 КГЭУ гр. ЭСм-1-17 Масса Масштаб Пояснительная записка Разраб. Исмагилов А.А. Провер. Муратаев И.А. Т. Контр. Н. Контр. Муратаев И.А. Утверд.                  Содержание: Содержание: Введение 2 1.«Выбор КУ в сложной сети» 4 2. «Оценка влияния напряжения на технико-экономические 10 показатели сети» 10 3.«Оптимальное распределение нагрузки между генераторами электростанции» 21 Заключение 29 Список использованной литературы 31 ВведениеПроблема оптимизации параметров и режимов систем передачи и распределения электроэнергии весьма сложна и многогранна. Задачи оптимизации параметров объектов приходится решать на стадии проектирования развития или конструкции электрической сети. Текущая оптимизация режимов осуществляет при эксплуатации сети. Проектирование, сооружение объектов электрической сети и их эксплуатация связаны с большими материальными затратами. Поэтому важно, чтобы эти затраты были использованы с наибольшей эффективностью. При этом следует учитывать, что правильность решений по развитию систем передачи и распределения электроэнергии, принимаемых в какой-то момент, может проявляться через достаточно длительное время, когда допущенные ошибки исправить невозможно или очень трудно. Дополнительные трудности при выработке решения связаны тем, что обычно присутствует неопределенность недостаточная достоверности исходной информации. Например, заранее точно обычно неизвестна перспективная нагрузка в каких-то узлах сети. При упрощенном подходе к решению такой задачи задаются тремя уровнями нагрузки (возможным наибольшим, возможны наименьшим и средним) и производят выбор параметров для всех этих уровней. Окончательное решение принимают на основе соответствующих приемов, описанных в специальной литературе. В любом случае для оптимизации параметров предварительно должен был выбран критерий оптимизации. Например качестве критериев могут выступать капитальные затраты, потери электроэнергии, пропускная способность сети, степень надежности электроснабжения, ее степень воздействия на окружающую среду и др. В простейшем случае многокритериальная задача сводится к однокритериальной в которой оптимизация параметров объекта осуществляется по одному критерии принятому за главный, а остальные критерии учитываются в виде ограничений.
Под сложной сетью в данном случае понимается сеть со многими узлами. В такой сети нельзя определить оптимальную мощность КУ в каждом узле, рассматривая его отдельно. Изменение потока реактивной мощности на каждом участке сети определяется КУ, установленными во всех ее узлах. Установка КУ в одном узле изменяет показатели эффективности их установки в других узлах. В этом случае ставится задача определения оптимального сочетания мощности и мест установки КУ, обеспечивающих минимум суммарных затрат. Такое решение должно также обеспечивать допустимые уровни напряжений в узлах. Последние обычно задаются ограничениями в форме неравенств (не ниже Uмин и не выше Uмакс). Для решения таких задач обычно используются градиентные методы оптимизации, реализующие итерационные алгоритмы постепенного приближения к оптимальному решению. Для определения направления движения к минимуму рассчитывают частные производные суммарных затрат (целевой функции) по мощности КУ в каждом узле. Физически они представляют собой удельные парциальные снижения суммарных затрат, руб./квар в год, при установке единичной мощности КУ в различных узлах. Далее малую мощность КУ (порцию КУ) распределяют между узлами пропорционально значениям производных. Очевидно, что при таком распределении большая часть порции КУ попадет в узлы с большими значениями производных, так как снижение реактивной мощности в этих узлах наиболее сильно снижает суммарные затраты. При новых значениях реактивной мощности в узлах вновь определяют частные производные, которые будут иметь меньшие значения, чем на предыдущем шаге. Следующую порцию суммарной мощности КУ распределяют между узлами пропорционально новым значениям производных и т.д. На каждом шаге оптимизации рассчитывают УР сети и проверяют соблюдение условия по допустимым уровням напряжения в узлах. В расчет вовлекаются также трансформаторы связи сетей различных классов напряжения, выбор оптимальных коэффициентов трансформации которых позволяет ввести уровни напряжения в узлах в допустимые пределы. При изменившихся через несколько итераций реактивных нагрузках узлов некоторые производные могут стать отрицательными, что говорит о завышенной мощности КУ, определенной для этих узлов на предыдущих итерациях. При распределении новой порции КУ в эти узлы будет добавляться отрицательная порция мощности КУ и мощность КУ в них снизится, а в узлах с положительными значениями производных продолжит увеличиваться. Расчет заканчивается, когда производные в узлах с накопившейся мощностью КУ становятся близкими к нулю, что говорит о том, что дальнейшее увеличение или уменьшение мощности КУ приведет только к увеличению суммарных затрат (достигнута точка 0 на рис. 7.1, а для всех узлов). Для проведения итерационных расчетов целевую функцию выразим через передаваемую в узел реактивную мощность, произведя замену Q = Qн - Qк и исключив неиспользуемую величину Рн: 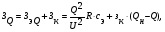 (1.1) (1.1)где Зэ Q — затраты на потери. Вектор частных производных (обозначим их для простоты σ) с использованием матричных обозначений имеет вид: 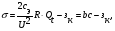 (1.2) (1.2)где 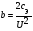 с — столбцевая матрица, элементами которой являются произведения i-й строки матрицы R и столбцевой матрицы Qt; зк — столбцевая матрица удельных годовых затрат на КУ (при одинаковых удельных затратах на КУ во всех узлах представляет собой столбец с одинаковыми значениями, равными Зк). Задание: выбрать оптимальные мощности КУ в узлах 1,2,3 при следующих условиях: TMAX=4000 час/год (число часов максимальных потерь); b0=2 руб/кВт*час (стоимость потерь электроэнергии), СЭ=2*4000=8000 руб/кВт=8 млн.руб/МВт; ККУ=800 руб/кВАр=0,8 млн.руб/МВАр(удельная стоимость КУ); Р0=5% (годовые затраты на обслуживание КУ в % от стоимости КУ); tок.пр.=5 лет. 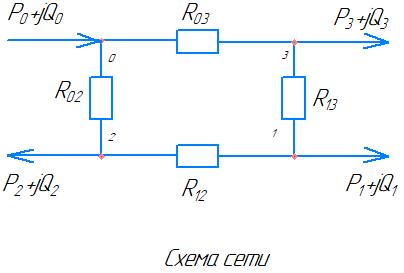 Рисунок 1.1. Схема сети Таблица 1.1 Исходные данные
Приведенные к году удельные затраты на КУ определяем по формуле: 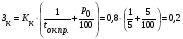 млн.руб./МВАр в год млн.руб./МВАр в годПри заданных условиях: 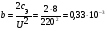 . .Значения узловых сопротивлений R определяется на основе предварительно составленной матрицы узловых проводимостей G, диагональные элементы которой представляют собой сумму проводимости ветвей, присоединенных к данному узлу, а каждый внедиагональный элемент является взятой со знаком минус проводимостью ветви, соединяющей данные узлы. Матрица узловых проводимостей: 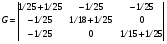 Матрица узловых сопротивлений для замкнутой сети определяется как обратная матрица G-1. Матрица узловых сопротивлений:  Подставим в формулу: 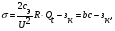 Получаем: 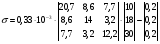 Вычислим значения элементов матрицы с: 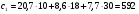 ; ;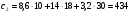 ; ;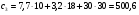 . .Умножая значения с на 0,33 ‧ 10-3 получим: 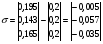 Численные значения элементов матрицы σ означают, что при установке единицы мощности КУ в первом узле суммарные годовые затраты снижаются на 0,005 млн руб., во втором на 0,057 млн руб., в третьем на 0,035 млн руб. Распределим между узлами суммарную мощность КУ, равную 10 Мвар. Распределяя ее пропорционально значениям производных, получим мощности КУ в узлах QК= 0,52; 5,88 и 3,61 Мвар. Реактивные нагрузки узлов Q=Qн - Qк станут равными 10,52; 23,88 и 33,61 Мвар. Таблица 1.2 Результаты итераций
|
