Краткий курс геометрии. Краткий курс геометрии 7 класс. Краткий курс геометрии 7 класс
 Скачать 368.84 Kb. Скачать 368.84 Kb.
|
Краткий курс геометрии 7 класс1. Простейшие геометрические фигуры и их свойства Аксиома. Основное свойство прямой: Через любые две точки можно провести прямую, и притом только одну. Определение. Пересекающиеся прямые: Две прямые, имеющие общую точку, называют пересекающимися. ТЕОРЕМА. О двух пересекающихся прямых: Любые две пересекающиеся прямые имеют только одну общую точку. Два отрезка называют равными, если их можно совместить наложением. Аксиома. Основное свойство длины отрезка: Если точка С является внутренней точкой отрезка АВ, то отрезок АВ равен сумме отрезков АС и т. е. АВ = АС + СВ. Расстоянием между точками называют длину отрезка АВ. Два луча, имеющие общее начало и лежащие на одной прямой, называют дополнительными. 2. Углы Углом называется геометрическая фигура (рис. 1), образованная двумя лучами, исходящими из одной точки. Точка О — вершина угла, а лучи ОА и ОБ — стороны угла. Обозначение: ∠AOB или ∠ab. Угол в 90° называется прямым (рис. 2). Угол, меньший прямого, называется острым (рис. 3). Угол, больший прямого, но меньший развернутого, называется тупым (рис. 4).  Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого (рис. 5). ∠AOC и ∠DOB; ∠BOC и ∠AOD — вертикальные. Вертикальные углы равны: ∠AOC = ∠DOB и ∠BOC = ∠AOD. Два угла называются смежными, если у них одна сторона общая, а две другие составляют прямую линию (рис. 6), ∠AOC и ∠BOC — смежные. 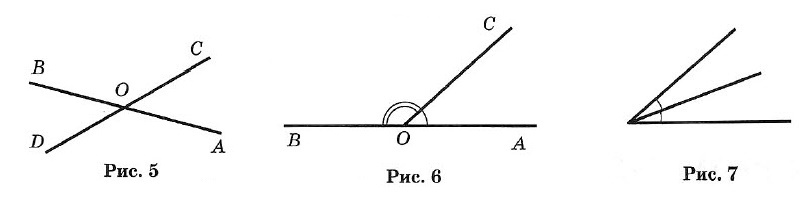 Сумма смежных углов равна 180°. Биссектрисой угла называется луч, проходящий между сторонами угла и делящий его пополам (рис. 7). Биссектрисы вертикальных углов составляют продолжение друг друга (рис. 8). Биссектрисы смежных углов взаимно перпендикулярны (рис. 9). 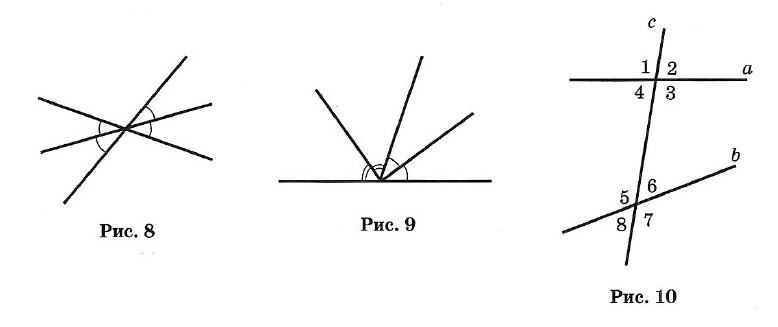 При пересечении двух прямых a и b третьей с (секущей) образуется 8 углов (рис. 10): соответственные углы: ∠1 и ∠5, ∠2 и ∠6, ∠4 и ∠8, ∠3 и ∠7; внутренние накрест лежащие: ∠4 и ∠6, ∠3 и ∠5; внешние накрест лежащие: ∠1 и ∠7, ∠2 и ∠8; внутренние односторонние: ∠4 и ∠5, ∠3 и ∠6; внешние односторонние: ∠1 и ∠8, ∠2 и ∠7. 3. Параллельные прямые Две прямые называют параллельными, если они не пересекаются. Аксиома параллельности прямых: Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Признаки параллельности двух прямых: • Две прямые, перпендикулярные третьей прямой, параллельны. • Если накрест лежащие углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны. • Если сумма односторонних углов, образующихся при пересечении двух прямых секущей, равна 180°, то прямые параллельны. • Если соответственные углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны. Свойства параллельных прямых: • Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны. • Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны. • Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180°. Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой. 4. Треугольник Треугольником называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Точки А, В, С — вершины треугольника АВС. Отрезки АВ, ВС и АС — стороны, ∠A, ∠B и ∠C — углы. ∠A + ∠B + ∠C = 180°. Стороны треугольника часто обозначают малыми буквами (рис. 13): АВ = с, ВС = а, АС = b. Р = а + b + с — периметр треугольника.  Треугольник, у которого все углы острые, называется остроугольным (см. рис. 13). Треугольник, у которого есть прямой угол, называется прямоугольным (рис. 14). Стороны, образующие прямой угол, называются катетами (а и b), а сторона, лежащая против прямого угла, — гипотенузой (с). Треугольник с тупым углом называется тупоугольным (рис. 15).  Треугольник, у которого две стороны равны, называется равнобедренным (рис. 16). Равные стороны называются боковыми, а третья сторона — основанием равнобедренного треугольника. Треугольник, у которого все стороны равны, называется равносторонним (рис. 17). Каждый угол равностороннего треугольника равен 60°. Свойства равнобедренного треугольника: 1. Углы при основании равны. 2. Биссектриса, проведенная к основанию, является одновременно медианой и высотой. 3. Высота, проведенная к основанию, является одновременно медианой и биссектрисой. 4. Медиана, проведенная к основанию, является одновременно высотой и биссектрисой. 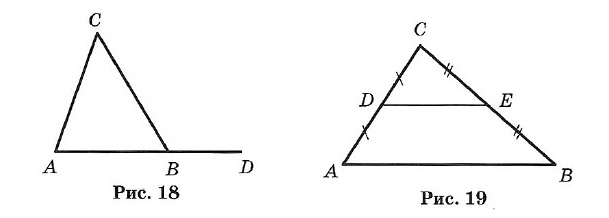 Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника (рис. 18). ∠CBD — внешний угол треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним (см. рис. 18): ∠CBD = ∠A + ∠C. Отрезок, соединяющий середины двух сторон, называется средней линией треугольника (рис. 19). 5. Признаки равенства треугольников I признак (признак равенства по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 20). АВ = А1В1, АС = А1С1, ∠A = ∠A1 II признак (признак равенства по стороне и прилежащим к ней углам). Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 21). АВ = A1B1, ∠A = ∠A1, ∠B = ∠B1 III признак (признак равенства по трем сторонам). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 22). АВ = А1В1, ВС = B1C1, АС =А1С1. 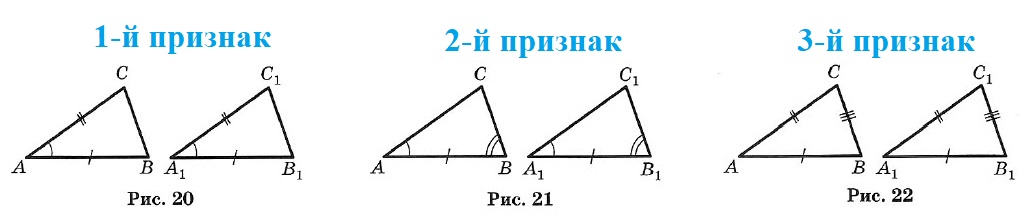 6. Соотношения между сторонами и углами треугольника ТЕОРЕМА о сумме углов треугольника. Сумма углов треугольника равна 180°. ∠A + ∠B + ∠C = 180°. ТЕОРЕМА о соотношениях между сторонами и углами треугольника. В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона. Следствие 1. В прямоугольном треугольнике гипотенуза больше катета. Следствие 2. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника). ТЕОРЕМА о неравенстве треугольника. Каждая сторона треугольника меньше суммы двух других сторон: а < b + с, b < а + с, с < а + b. 7. Прямоугольные треугольники (некоторые свойства) 1. Сумма острых углов равна 90° (рис. 23). ∠A + ∠B = 90°. 2. Катет, лежащий против угла в 30°, равен половине гипотенузы (рис. 24). a = c/2 3. Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30° (рис. 24). 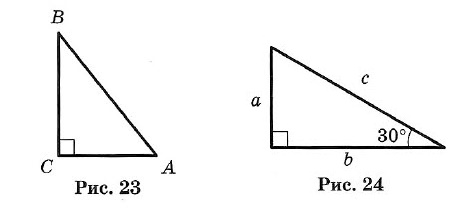 8. Признаки равенства прямоугольных треугольников 1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис. 25). АС = А1С1, ВС = В1С1. 2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны (рис. 26). АС = А1С1, ∠A = ∠A1. 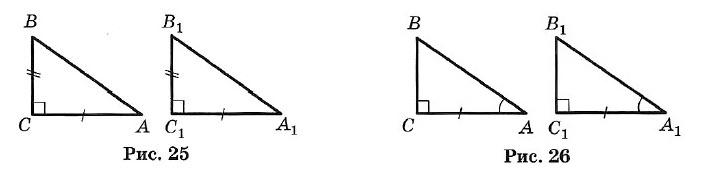 3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны (рис. 27). АВ = А1В1, ∠A = ∠A1. 4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны (рис. 28). АВ = А1В1, АС = А1С1 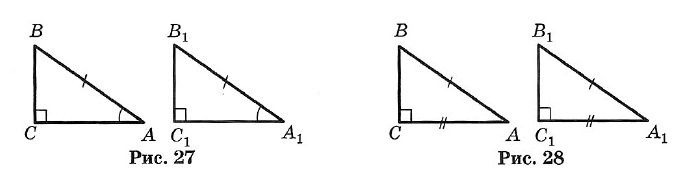 10. Четыре замечательные точки треугольника С каждым треугольником связаны 4 точки: 1) точка пересечения медиан; 2) точка пересечения биссектрис; 3) точка пересечения высот (или их продолжений); 4) точка пересечения серединных перпендикуляров к сторонам. Эти четыре точки называются замечательными точками треугольника. Высотой треугольника называется длина перпендикуляра, опущенного из любой его вершины на противолежащую сторону или ее продолжение. 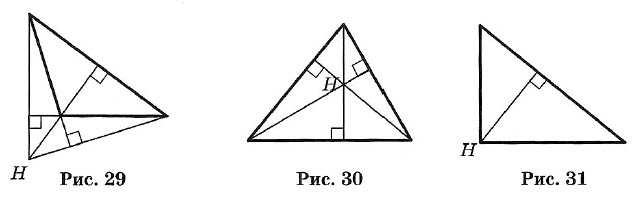 В тупоугольном треугольнике (рис. 29) две высоты падают на продолжение сторон и лежат вне треугольника, а третья внутри. В остроугольном треугольнике (рис. 30) все три высоты лежат внутри треугольника. В прямоугольном треугольнике катеты одновременно служат и высотами (рис. 31). Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром. В тупоугольном треугольнике ортоцентр лежит вне треугольника. В прямоугольном треугольнике он совпадает с вершиной прямого угла. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. 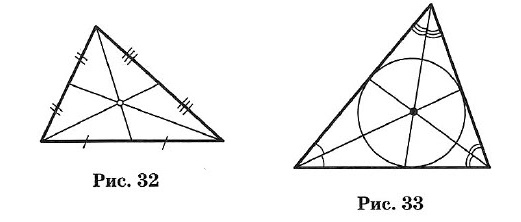 Три медианы треугольника пересекаются в одной точке, которая является центром тяжести треугольника (рис. 32). Эта точка делит каждую медиану в отношении 2 : 1 (считая от соответствующей вершины). Биссектрисой треугольника называется отрезок биссектрисы угла от вершины до пересечения с противолежащей стороной. Три биссектрисы треугольника пересекаются в одной точке, которая является центром вписанного круга (рис. 33). Три перпендикуляра к сторонам треугольника, проведенные через их середины (рис. 34, 35, 36), пересекаются в одной точке, которая является центром описанной окружности. 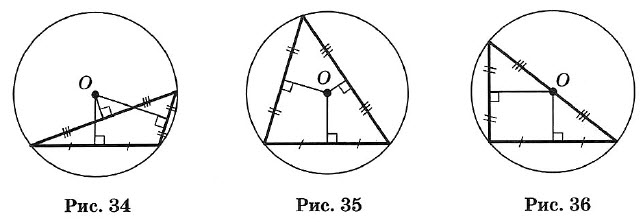 В тупоугольном треугольнике (рис. 34) эта точка лежит вне треугольника, в остроугольном (рис. 35) — внутри, в прямоугольном — на середине гипотенузы (рис. 36). Ортоцентр, центр тяжести, центр вписанной и описанной окружностей совпадают друг с другом только в равностороннем треугольнике. 11. Окружность 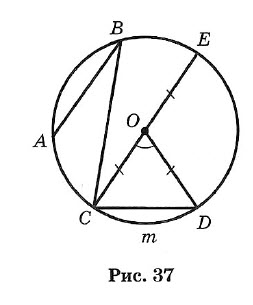 Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37). Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R. На рисунке ОС = ОЕ = OD = R. Часть окружности (например, CmD) называется дугой. Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром. АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр. Обозначение: d или D. D = 2R. Часть плоскости, ограниченная окружностью, называется кругом. Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом. Часть круга, ограниченная двумя радиусами и дугой, называется сектором. Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37). Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC). 12. Свойства касательных к окружности Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38). 1. Радиус, проведенный в точку касания, перпендикулярен касательной. 2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними. 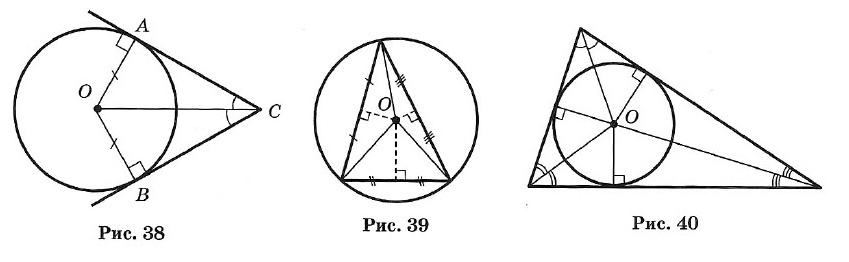 13. Окружность и треугольник 1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39). 2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40). |
