Кудрявцев Павел Степанович Курс истории физики
 Скачать 7.55 Mb. Скачать 7.55 Mb.
|
 В 1867г. Больцман кончает университет и публикует работу «О числе атомов в молекуле газа и внутренней работе в газе». В 1868 г. он издает большую работу «Исследование равновесия живых сил движущихся материальных точек» и другие статьи. Талант крупного теоретика настолько ясно выразился в этих ранних работах Больцмана, что в следующем, 1869 г. двадцатипятилетний Больцман избирается профессором физики в Граце. Отметим, что в Граце Больцман руководил кафедрой экспериментальной физики, на которой была уже создана прекрасная физическая лаборатория, оборудованная всем необходимым как для научных исследований, так и для студенческого практикума. Он занимает здесь кафедру до 1873 г., затем возвращается в Вену, чтобы занять здесь кафедру математики. В Вене Больцман пробыл всего три года и в 1876 г. вновь возвращается в Грац, где остается до 1889 г. В этот период он выполняет свои важнейшие работы по статистической физике. С 1889 по 1894 г. Больцман – профессор в Мюнхене, с 1894 по 1900 г. Больцман опять в Вене, откуда уезжает на два года (1900–1902) в Лейпциг. В 1902 г. Больцман возвращается в Вену, где живет до своей смерти, последовавшей 16 сентября 1906 г. Фундаментальным вкладом Больц-мана в физику является создание статистической механики и статистического обоснования второго начала. Уже в ранней работе «Исследование равновесия живых сил движущихся материальных точек» Больцман ставит задачу «найти общую теорему для вероятности распределения положений и скоростей таких движущихся материальных точек». Для случая частиц, находящихся в сильном поле, потенциальная энергия которого зависит от координаты х и равна f(x), Больцман находит, что «вероятность того, что х находится между х и х + dx..., пропорциональна », и вероятность того, что скорость лежит между с и с + dс, «для каждого х пропорциональна ». Таким образом, Больцман уже в возрасте двадцати четырех лет нашел закон распределения, носящий теперь его имя. Больцман, основываясь на работе Максвелла, обобщил его закон распределения, рассматривая газ в силовом поле. Дальнейшее обобщение Больцман сделал в работе «О тепловом равновесии многоатомных молекул газа». «Для случая, когда каждая молекула является одной материальной точкой, – писал Больцман, – Максвелл определил вероятность различных состояний». Больцман выписывает закон Максвелла в виде: 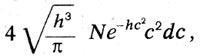 где N - число молекул в единице объема, с - скорость молекул, h - константа, определяемая температурой. «Но встречающиеся в природе молекулы, – писал Больцман, – отнюдь не являются простыми материальными точками. Мы, очевидно, будем ближе к действительности, если будем рассматривать их как систему нескольких материальных точек (так называемых атомов), которые удерживаются вместе определенными силами. Тогда состояние молекулы в определенный момент времени будет определяться не одной переменной, а многими». Максвелл в 1875 г. в статье «О динамическом доказательстве молекулярного строения тел» присоединяется к результатам Больцмана. Он писал: «Опубликованные мной в 1860 г. результаты подверглись затем более строгому исследованию доктора Людвига Больцмана, применившего также свой метод к изучению движения сложных молекул». Указав на трудности теории теплоемкости, Максвелл считает, что теорема Больцмана дает возможность объяснить закон Дальтона, выравнивание температур в вертикальном столбе газа и «открывает, по-видимому, путь в чисто химическую область исследования». Критические замечания Максвелла о кинетической теории теплоемкости также примыкают к рассуждениям Больцмана. Больцман показал, что средняя кинетическая энергия всех атомов, которые считаются точками, одна и та же и равна 3/2h. Отсюда для двухатомных молекул отношение теплоемкостей Ср /Сv должно равняться 1,33, а опыт дает для воздуха 1,41. Больцман считает это расхождение обусловленным взаимодействием молекул с эфиром. Максвеллу это объяснение кажется сомнительным. В 1876 г. Больцман уточнил свою теорию теплоемкости. В статье «О природе газовых молекул» он указал на про тиворечие своей теории с опытом и сослался на обобщение его теоремы, сделанное Максвеллом и Уатсоном. Максвелл и Уатсон понимали молекулу как систему, положение которой определяется т переменными величинами, не зависящими от движения молекул. Это число т называется числом степеней свободы. Для одноатомной молекулы число степеней свободы равно 3 и отношение теплоѐмкостей равно 1и2/3. Для двухатомных молекул число степеней свободы равно пяти: «три координаты центра тяжести и две переменных, определяющих направление центральной линии молекулы». Поэтому для них оно будет λ`/λ=1,4. Если молекулу представлять как твердое тело с шестью степенями свободы, то λ`/λ =1,33. Теорема Больцмана о равномерном распределении кинетической энергии по степеням свободы молекулы, лежащая в основе классической теории теплоемкости, является важным результатом статистики Больцмана. Однако важнейшим результатом многолетних исследований Больцмана по кинетической теории газов было открытие им связи между энтропией и вероятностью. Упорные поиски механического обоснования второго начала термодинамики увенчались успехом. Но это обоснование потребовало введения понятия вероятности и было достигнуто на путях развития статистической механики. Формулировка, развитие и защита «теоремы– Н», которая выражает связь между энтропией и вероятностью данного состояния системы, составили дело жизни Больцмана. Оно началось с его юношеской работы 1866 г. и продолжалось до последней статьи «Кинетическая теория материи», написанной is сотрудничестве с Ноблем для «Математической энциклопедии». Статья была закончена в октябре 1905 г., и выпуск «Энциклопедии», в котором она была опубликована, был снабжен кратким сообщением «Памяти Людвига Больцмана», начинавшимся словами: «В этом выпуске на первом месте помещена статья Больцмана о кинетической теории материи и вместе с тем это последнее создание его рук». Основная работа, в которой Больцман впервые формулирует свою теорему, – это работа 1872 г. «Дальнейшее исследование теплового равновесия газовых молекул». Здесь Больцман со всей четкостью утверждает, что «проблемы механической теории теплоты являются проблемами статистическими». Больцман выводит основное уравнение для функции распределения f и показывает, что существует такая функция Е, зависящая от логарифма f, которая всегда убывает и лишь при достижении статистического равновесия остается постоянной. В этом состоянии равновесия функция распределения совпадает с максвелло-больцмановским распределением. В статье 1877 г. «О связи второго начала механической теории теплоты с исчислением вероятностей» Больцман подробно развивает свой статистический метод. Он указывает в самом начале статьи, что связь между вторым началом термодинамики и исчислением вероятностей «обнаруживается прежде всего в том, что, как мною было показано, аналитическое доказательство второго начала невозможно никакими другими способами, кроме тех, которые заимствуются из теории вероятностей». Чрезвычайно интересно с исторической точки зрения введение Больцманом в этой работе гипотезы, что молекула газа может терять и приобретать только дискретные порции энергии, кратные некоторой наименьшей порции энергии ε. «Перед столкновением, – пишет Больцман, – каждая из обеих сталкивающихся молекул имеет живую силу 0, или ε, или 2ε и т. д. или pε и вследствие какой-то причины будет происходить то, что и после соударения никогда ни одна из сталкивающихся молекул не принимает живой силы, не содержащейся в этом ряде». Так Больцман начинает свои статистические рассуждения, оговариваясь, однако, что это фикция, которой не соответствует ничего реального, но которая облегчает математическую трактовку проблемы. В дальнейших вычислениях Больцман освобождается от гипотезы, полагая в пределе эпсилон ε=0. Больцман ставит задачу найти закон распределения, который позволяет знать, как много из общего числа молекул n обладает энергией 0, ε, 2ε,. Он подсчитывает, сколько комбинаций соответствует такому распределению состояний, полагая, что число этих комбинаций определяет вероятность данного состояния. Если бы Больцман считал молекулы газа неразличимыми, как это делал в квантовой теории идеального газа Эйнштейн, и сохранил предположение о конечной порции энергии, то он получил бы формулу статистики Бозе–Эйнштейна. Но Больцман этого не сделал. Он считал неразличимыми между собой молекулы, находящиеся в одном и том же энергетическом состоянии. Однако когда молекула одной энергетической группы меняется местами с молекулой другой энергетической группы, то, хотя распределение молекул не меняется, тем не менее возникает новая комплексия. Число комплексий, которым может быть осуществлено данное состояние, и определяет, по Болыдману, вероятность этого состояния. Таким образом, она, по Больцману, определяется числом: 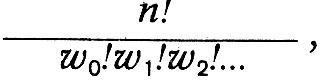 где n - общее число молекул, w0 - число молекул, обладающих энергией, равной нулю (Больцман считает энергию между 0 и ε, отступая от первоначальной квантовой гипотезы), w1, – число молекул, обладающих энергией ε (между ε и 2ε), и т. д. При этом и общая энергия Логарифмируя выражение для вероятности и определяя максимум этой логарифмической функции при условии постоянства n и L, Больцман находит распределение Максвелла – Больцмана, которое оказывается, таким образом, наиболее вероятным распределением. Подсчитывая наиболее вероятное распределение скоростей, Больцман вводит величину Θ, равную среднему логарифму функции распределения, взятой со знаком минус. Максимальное значение этой величины, которую Больцман называет «мерой распределения», при условии постоянства числа молекул и их общей кинетической энергии определяет наиболее вероятное распределение. Величину, которую Больцман обозначал через Е и Θ, в дальнейшем стали обозначать Н, и она оказалась пропорциональной энтропии. Закон возрастания энтропии у Больцмана получает простую интерпретацию: «Система стремится к наиболее вероятному состоянию». Второе начало потеряло характер абсолютного закона природы и стало статистическим законом. В природе возможны процессы, происходящие в направлении убывания энтропии, и это, по мнению Больцмана, избавляет Вселенную от тепловой смерти. Для космоса в целом тепловой смерти нет. Взгляды и выводы Больцмана подвергались ожесточенной критике. Но вместе с тем они воспринимались и развивались другими исследователями: Максвеллом, Лоренцем, Планком. Планк дал простой вывод и простое точное выражение соотношения между энтропией и вероятностью. В обозначениях Планка оно имеет вид: S = k lnW, где S - энтропия, W - вероятность, k -постоянная, равная R/N, которую Планк назвал в честь Больцмана постоянной Больцмана. Из соотношения Планка исчезла неопределенная аддитивная константа, фигурирующая у Больцмана, и это соответствует тепловой теореме Нернста. формула соотношения между энтропией и вероятностью, данная Планком, фигурирует сегодня во всех руководства и монографиях как соотношение Больцмана. В 1912 г., читая лекции по статистическим теориям термодинамики в Париже, Лоренц говорил об успехах кинетической теории газов. Он указывал, как бы подводя итоги многолетней борьбы сторонников феноменологического описания с приверженцами атомистики: «Теперь нельзя сомневаться в их существовании после того, как «реальность молекул» стала фактом, почти что «наблюдаемым» непосредственно; молекулы существуют для нас совершенно так Же, как и многие другие предметы, непосредственно нами не видимые, но в существовании которых наш ум вовсе не сомневается». Далее Лоренц продолжал: «Основываясь на этих блестящих результатах, можно поставить вопрос: нельзя ли найти закон Карно – Клаузиуса при помощи молекулярных теорий, понимая, конечно, последние в очень широком смысле, так как общности результата должна каким-либо образом соответствовать общность предпосылок? Австрийскому физику Больцману принадлежит честь первого успешного подхода к этой задаче и установление связи между понятием вероятности, определенным образом понимаемой, и термодинамическими функциями, в частности энтропией. Рядом с ним нужно считать одним из основателей этой новой ветви теоретической физики – статистической термодинамики – Уилларда Гиббса. Далее следует упомянуть работы Пуанкаре, Планка и Эйнштейна. Общий результат, который можно считать окончательно установленным, это существование связи между энтропией некоторого состояния и вероятностью этого состояния». К именам, упомянутым Лоренцем, следует добавить имена П.Эренфеста и Т. А. Афанасьевой-Эренфест, которым принадлежит ряд работ по статистической термодинамике, и в частности фундаментальная обзорная статья о принципиальных основах статистического понимания, опубликованная в «Математической энциклопедии» в 1911 г. Все эти работы относятся к более позднему времени. Больцман же мог прочитать и оценить лишь книгу Гиббса «Основные принципы статистической механики», вышедшую в 1902 г. Он пришел также к пониманию идей Планка, как об этом писал сам Планк в своей автобиографии. Но все это происходило уже в XX в., когда физика переходила на новые пути, переживая мучительный кризис старого, «классического» понимания природы. В период жизни Больцмана был один физик, разрабатывавший проблемы, которыми занимался и Больцман, и внимательно следивший за его работами. Это был сын знаменитого русского хирурга Н.И.Пирогова Н. Н. Пирогов (1843–1891). В ряде работ, публиковавшихся в Журнале русского физико-химического общества за 1885-1890 гг., Пирогов рассматривал проблемы кинетической теории газов и статистической термодинамики. В них он не только защитил результаты Болыдмана, но и уточнил и развил и-х, сформулировав ряд важных идей, найденных статистической физикой позже. К сожалению, работы Пирогова, публиковавшиеся на русском языке, остались малоизвестными и не оказали своевременного влияния на развитие статистической термодинамики. Советские историки физики «открыли» Н. Н. Пирогова лишь в конце сороковых годов XX в..( См.: Спасский Б. И. Н. Н Пирогов.–Вкн.:Развитиефизики вРоссии.–М.:Просвещение, 1970, с. 300-308.)  Остановимся в заключение на развитии представлений о самом атоме. Максвелл, Клаузиус, Больцман, Гиббс, развивая физическую атомистику, искали законы, управляющие поведением коллектива атомов и молекул, делая по возможности простые гипотезы о строении самих атомов. В XIX в. единственным средством наблюдать взаимодействия атомов и определять их индивидуальные особенности были химические реакции. Именно в недрах химической атомистики родилась первая гипотеза о строении всех атомов из атомов водорода (Проут, 1815). Химия выработала учение об элементе, определила атомные веса различных атомов, установила характерные особенности различных элементов. В 1859 г. было сделано важное открытие в оптике, физик Густав Кирхгоф (1824–1887) и химик Роберт Бунзен (1811–1899) открыли спектральный анализ, давший в руки химикам новое мощное средство исследования. Отметим, что это открытие было сделано в Гейдельбергской физической лаборатории сначала с флинт-призмой, отшлифованной самим фраунгофером, а затем со спектральным аппаратом с четырьмя фраунгоферовыми призмами, сконструированными Кирхгофом совместно с Бунзеном. Сами Кирхгоф и Бунзен методом спектрального анализа обнаружили элементы цезий (1860) и рубидий (1861). В 1861 г Крукс открыл спектроскопическим путем таллий. Через два года Райх и Рихтер обнаружили индий. Чрезвычайно интересна история открытия гелия. Кирхгофу впервые удалось раскрыть загадку фраунгоферовых линий и показать, что они получаются в результате поглощения лучей, испускаемых Солнцем, элементами, входящими в состав солнечной атмосферы. Так было доказано присутствие на Солнце ряда химических элементов. При наблюдении во время затмения соответствующие линии ярко вспыхивают в спектре Солнца. Наблюдая в 1868 г полное солнечное затмение, французский астроном Жан сен и английский астроном Локьер независимо друг от друга открыли в спектре Солнца яркую желтую линию, не принадлежащую ни одному из известных на Земле элементов. Локьер предположил, что эта линия испускается элементом, встречающимся только на Солнце, который он предложил поэтому назвать гелий (от греческого «гелиос» – Солнце) В 1895 г. английский химик Рамзей, исследуя спектроскопически газы, выделяющиеся при обработке кислотой минерала клевеита, нашел желтую линию гелия, который он в том же году выделил химически из газовой смеси. В 1869 г. было известно 63 хими ческих элемента. В этом же году Д.И.Менделеев открыл фундаментальный закон распределения элементов в систему, которую он назвал периодической системой химических элементов. Д.И.Менделеев родился 8 февраля 1834 г. в семье директора Тобольской гимназии. Д.И.Менделеев учился на физико-математическом факультете Петербургского педагогического института. Среди его учителей были известный математик М. В. Остро градский, физик Э.Х. Ленц, «отец русских химиков» А. А. Воскресенский. В этой обстановке научное дарование Менделеева развивалось быстро – и уже студентом он выполнил первую работу о химическом составе минералов ортита и пироксена. Институт он окончил с золотой медалью в 1855 г. и по состоянию здоровья вынужден был уехать в Крым, а затем в Одессу, где работал учителем гимназии. На юге здоровье Менделеева восстановилось, и в 1856 г. он вернулся в Петербург. Успешно сдав магистерские экзамены, он защитил диссертацию «Об удельных объемах». Затем он защитил диссертацию «О строении кремнеземистых соединений» на звание доцента Петербургского университета, в котором в 1857–1858 гг. читал курс теоретической и органической химии. В январе 1859 г. Менделеев был командирован за границу. Там он работал в лабораториях Бунзена, Кирхгофа и Коппа, а также в организованной им домашней лаборатории, в которой выполнил свое исследование по абсолютной температуре кипения. В 1860 г. Менделеев принял участие в съезде химиков в Карлсруэ, где Канниццаро, к которому примкнул и Менделеев, защищал теорию Авогадро – Жерара и новое определение атомных весов. С этого съезда химики стали правильно определять атомные веса элементов,  что имело огромное значение для будущего великого открытия Менделеева. что имело огромное значение для будущего великого открытия Менделеева.После двухлетнего пребывания за границей Менделеев вернулся в Петербург и приступил к чтению курса органической химии в университете. В 1867 г. А.А.Воскресенский уехал в Харьков попечителем учебного округа, и Менделеев занял освободившуюся кафедру неорганической химии Петербургского университета. При подготовке к чтению лекций университетского курса химии Менделеев рассуждал о связи между химическими элементами и составил их картотеку, раскладывая карточки «наподобие пасьянса». Он обратил внимание на периодичность в расположении атомных весов и повторяемости свойств элементов. 17 февраля 1869 г. Д. И. Менделеев составил карточку «Опыт системы элементов», которую и разослал некоторым химикам. Сообщение Д.И.Менделеева Русскому химическому обществу «Соотношение химических свойств с атомным весом элементов» сделал 6 марта (ст. стиля) 1869 г. Н.А.Меншуткин. В этом сообщении Менделеев излагал историю вопроса и причины, побудившие его им заняться. «Предприняв составление руководства к химии, названного «Основы химии», – писал Менделеев, – я должен был остановиться на какой-нибудь системе простых тел, чтобы в распределении их не руководствоваться случайными, как бы инстинктивными, побуждениями, а каким-либо точным началом». Указав, что со времен Жерара и Канниццаро уж нет сомнения в значении атомных весов элементов, «как это было несколько лет тому назад, когда атомный вес столь часто смешивался с эквивалентом и определялся на основании разнородных часто противоположных начал», Менделеев пишет, что он «старался основать систему по величине атомного веса элементов». Приведя результаты предпринятых им проб, которые показали, что между естественными свойствами элементов и величиной атомного веса существует некоторое точное отношение, Менделеев заключает: «Все сличения, сделанные мною в этом направлении, приводят меня к тому заключению, что величина атомного веса определяет природу элемента настолько же, насколько вес частицы определяет свойства и многие реакции сложного тела. Если это убеждение подтвердится дальнейшим применением выставленного начала, то мы приблизимся к эпохе понимания существенного различия и причины сходства элементарных тел». Далее Менделеев пишет: «Отныне, мне кажется, приобретается еще новый интерес в определении атомных весов, в открытии новых простых тел и в отыскании новых между ними аналогий». Так, уже в первом наброске системы, которую сам Менделеев не считал «совершенно законченной», он ясно видел, что открытый им закон приближает эпоху «понимания существенного различия и причины сходства элементарных тел» и что он может служить путеводным началом в открытии новых, еще неизвестных элементов. Менделеев в этом сообщении со всей определенностью писал: «Должно ожидать открытия еще многих неизвестных простых тел, например сходных с А1 и Si элементов с паем 65–75». В качестве первого вывода из своего исследования Менделеев записал: «Элементы, расположенные по величине их атомного веса, представляют явственную периодичность их свойств». Такова первая формулировка периодического закона, сыгравшего фундаментальную роль в истории атомной и ядерной физики. Менделеев продолжал работать над развитием и укреплением своего закона. 3 декабря 1870 г. он выступил в заседании Русского химического общества с сообщением «Естественная система элементов и ее применение к указанию свойств некоторых элементов». Он предсказал существование экабора, открытого шведским химиком Ниль-соном в 1879 г., названного скандием, экаалюминия, открытого французским химиком Лекок де Буабодраном под названием талий в 1875 г., и экакремния, открытого в 1886 г. немецким химиком Винклером под названием германий. Открытие периодического закона и предсказание на его основе новых элементов было высоко оценено Энгельсом, которьй назвал открытие Менделеева научным подвигом и сравнил его с предсказанием Леверье планеты Нептун. Это была очень высокая оценка– закон Менделеева оказался по своей точности и силе сравнимым с законами небесной механики. Эта оценка оправдалась и в дальнейшей истории закона: со времени его открытия было найдено свыше сорока новых элементов с самыми различными свойствами, и все они оказались включенными в систему Менделеева, а при открытии трансурановых элементов она служила руководящей нитью. Американские ученые во главе с Сиборгом, открыв в 1955 г. элемент № 101, назвали его менделевий «в знак признания пионерской роли великого русского химика Дмитрия Менделеева, который первым использовал периодическую систему для предсказания химических свойств еще не открытых элементов – принцип, который послужил ключом для открытия последних, или трансурановых элементов». Великий автор периодического закона отличался необычайной разносторонностью и широтой научной и общественной деятельности. Он был профессором Петербургского университета, в котором совместно с А. М. Бутлеровым и Н. А. Меншуткиным провел всю подготовительную работу по созданию новой химической лаборатории, которая была построена в 1891–1894 гг., когда А.И.Менделеева уже не было в университете. Он был вынужден уйти из университета в начале 1890 г. в знак протеста против действий министерства народного просвещения в связи со студенческими волнениями. В 1893 г А И Менделеев был назначен хранителем Палаты мер и весов, которая под его руководством превратилась в первоклассное научно-метрологическое учреждение – Главную палату мер и весов, ныне Всесоюзный научно-исследовательский институт метрологии и стандартизации (ВНИИМС). Д. И.Менделеева глубоко интересовало развитие промышленности и экономики России. Этому он посвятил немало трудов, активно участвуя в различных правительственных комиссиях, в том числе и по выработке таможенного тарифа. Нефтяное дело, металлургия, заводское дело, земледелие, промышленное развитие России, ее народонаселение–все интересовало ученого, везде он оставил свой неизгладимый след. Кипучая, разносторонняя деятельность Дмитрия Ивановича Менделеева оборвалась в 1907 г. 20 января 1907 г. он скончался в Петербурге от воспаления легких. С открытием спектрального анализа и периодического закона химических элементов стало ясно, что атом представляет сложную структуру с внутренними движениями его составных частей, порождающих характерные спектры. Но прежде чем приступить к изучению этой структуры, физике предстояло сделать новый шаг в развитии электромагнитной теории. Этот шаг был сделан Максвеллом. |
