5.3. Структурная схема лопастной ветроэлектрической
установки и ее основные технические параметры
Л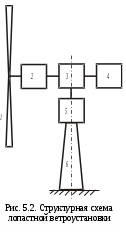 опастная ветроустановка состоит из следующих основных элементов (рис. 5.2): 1 – ветроколесо, 2 – регулятор установки лопастей ветроколеса, который обеспечивает изменение угла поворота лопасти пропорционально изменению скорости ветра и вывод лопастей во флюгерное положение (отключение агрегата) при достижении аварийной скорости ветра, 3 – редуктор, который обеспечивает подключение электрогенератора с соответствующей мощностью и необходимую частоту вращения ротора генератора (50 Гц.), 4 – электрический генератор, 5 – механизм поворота оси ветроколеса параллельно ветровому потоку, 6 – опора. опастная ветроустановка состоит из следующих основных элементов (рис. 5.2): 1 – ветроколесо, 2 – регулятор установки лопастей ветроколеса, который обеспечивает изменение угла поворота лопасти пропорционально изменению скорости ветра и вывод лопастей во флюгерное положение (отключение агрегата) при достижении аварийной скорости ветра, 3 – редуктор, который обеспечивает подключение электрогенератора с соответствующей мощностью и необходимую частоту вращения ротора генератора (50 Гц.), 4 – электрический генератор, 5 – механизм поворота оси ветроколеса параллельно ветровому потоку, 6 – опора.
Передача мощности на горизонтальноосевых установках осуществляется от лопастей через втулку, на больших установках, через многоступенчатый редуктор и, с промежуточным включением элементов сцепления, на генератор. К этому добавилась другая важная подсистема с высокими требованиями к механике и системе управления механизмом поворота в направлении ветра, а у многих современных установок – и механизмом изменения угла лопастей. Эта, значительная, механическая часть установки обуславливает, как правило, в большой степени надежность, необходимость в техническом обслуживании и срок жизни установки.
Одним из наиболее важных показателей работы ветроустановки является ее мощность:
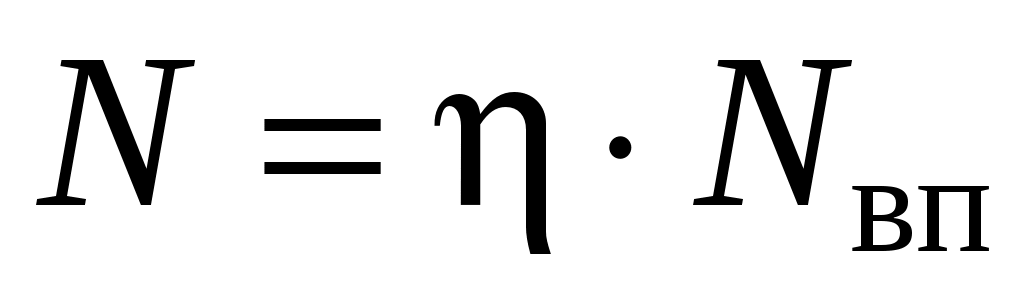
где 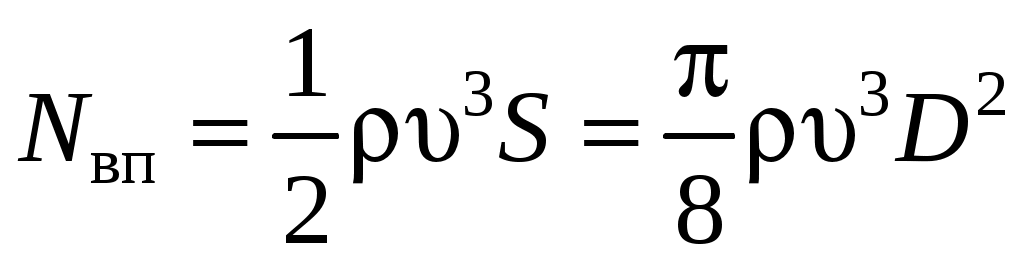 – мощность ветрового потока, Вт; S – оме- – мощность ветрового потока, Вт; S – оме-
таемая площадь ветроколеса, м2; D – диаметр ветроколеса, м; 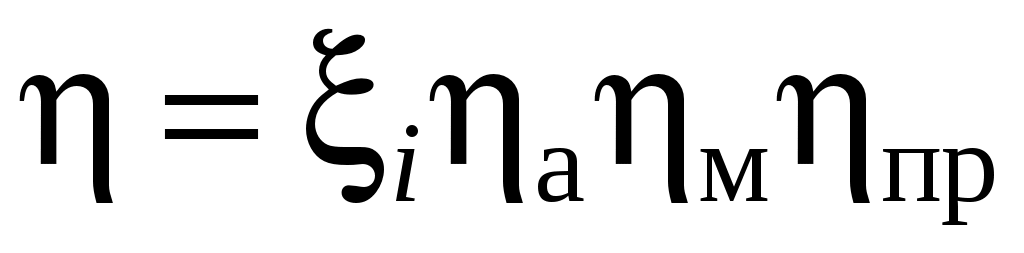 – КПД ветровой установки, – КПД ветровой установки, 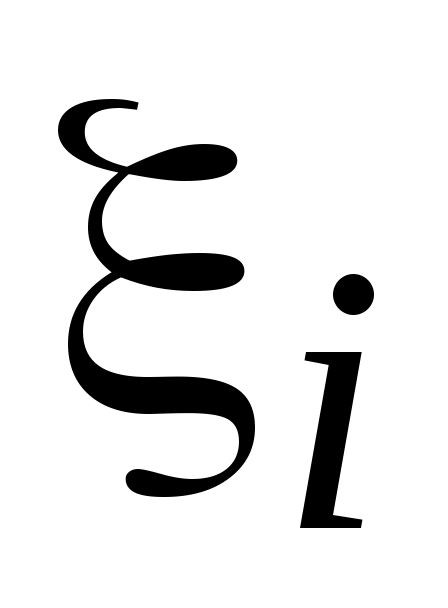 – коэффициент использования ветра идеальным ветроколесом, который представляет собой отношение мощности идеального ветроколеса (т.е при отсутствии аэродинамических потерь) к мощности ветрового потока проходящего через сечение равное ометаемой площади ветроколеса; – коэффициент использования ветра идеальным ветроколесом, который представляет собой отношение мощности идеального ветроколеса (т.е при отсутствии аэродинамических потерь) к мощности ветрового потока проходящего через сечение равное ометаемой площади ветроколеса; 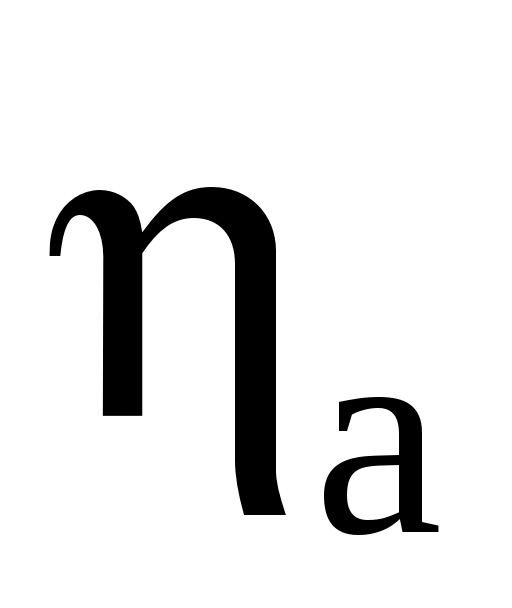 – коэффициент аэродинамических потерь в ветроколесе; – коэффициент аэродинамических потерь в ветроколесе; 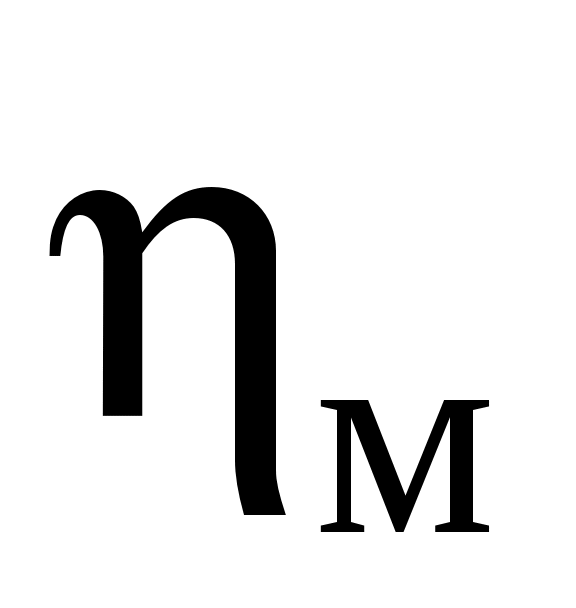 – коэффициент механических потерь (редуктор, подшипник); – коэффициент механических потерь (редуктор, подшипник); 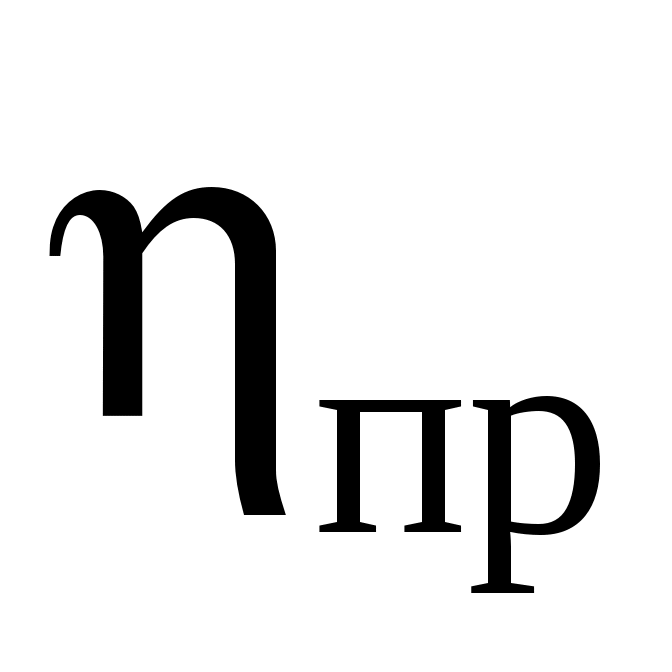 – коэффициент потерь в системе преобразования энергии после редуктора. – коэффициент потерь в системе преобразования энергии после редуктора.
Чтобы при увеличении скорости ветра ограничить повышение числа оборотов и мощности, современные ветродвигатели имеют автоматические системы регулирования. Наиболее широко применяют систему регулирования выводом ветроколеса из-под ветра и поворотом лопасти относительно ее продольной оси. Последняя система регулирования более простая и менее затратная. В зависимости от регулирующего фактора (лобовой или центробежной силы) влияющего на угол установки лопасти она делится на два вида: аэродинамическая и центробежная.
5.4. Работа поверхности при действии на нее силы ветра
Посмотрим, сколько процентов энергии ветра может превратить в полезную работу поверхность, поставленная перпендикулярно к направлению ветра и перемещающаяся в этом же направлении, что имеет место, например, у ветродвигателей карусельного типа.
Р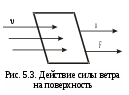 ассмотрим поверхность площадью S, поставленную перпендикулярно к направлению ветра. Воздушный поток вследствие торможения его поверхностью получит подпор и будет обтекать её и производить давление силой F. Вследствие действия этой силы поверхность будет перемещаться в направлении потока с некоторой скоростью u(рис. 5.3). ассмотрим поверхность площадью S, поставленную перпендикулярно к направлению ветра. Воздушный поток вследствие торможения его поверхностью получит подпор и будет обтекать её и производить давление силой F. Вследствие действия этой силы поверхность будет перемещаться в направлении потока с некоторой скоростью u(рис. 5.3).
Мощность N, получаемая пластиной, определяется произведением силы Fна скорость u, с которой перемещается поверхность:
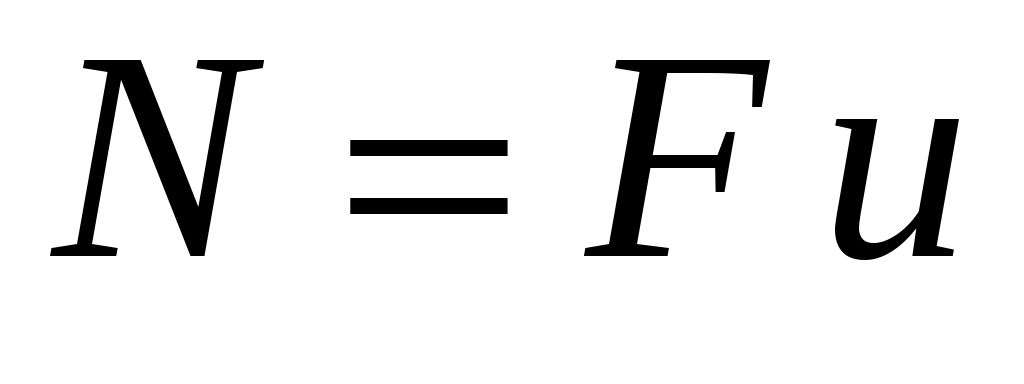 . .
В этом случае ветер набегает на поверхность с относительной скоростью, равной:
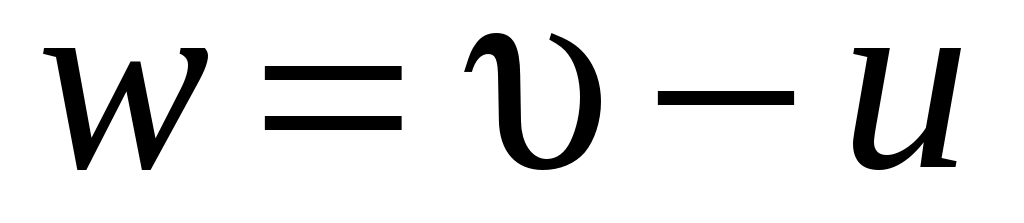 . .
Тогда сила сопротивления без учета ародинамических потерь равна:
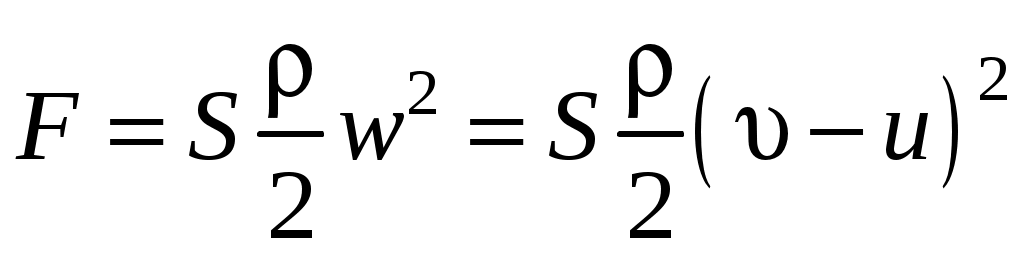 . .
Подставим выражение для силы F в уравнения для мощности:
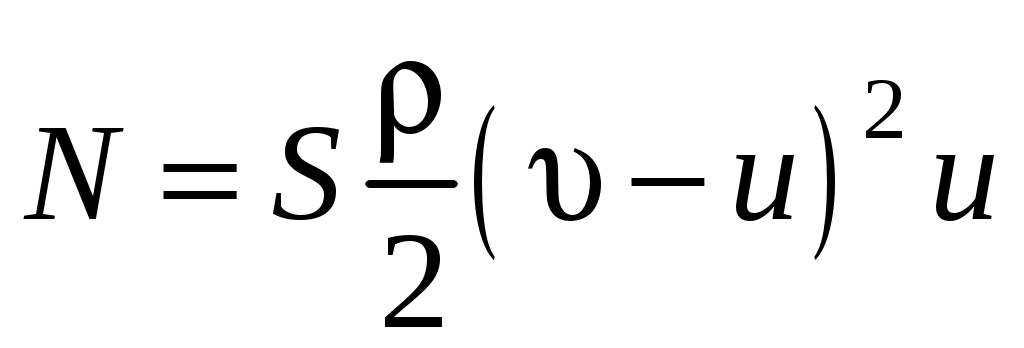 . .
Определим коэффициент использования энергии, т. е. отношение работы, развиваемой движущейся поверхностью, к энергии ветрового потока, имеющего поперечное сечение, равное этой поверхности, а именно:
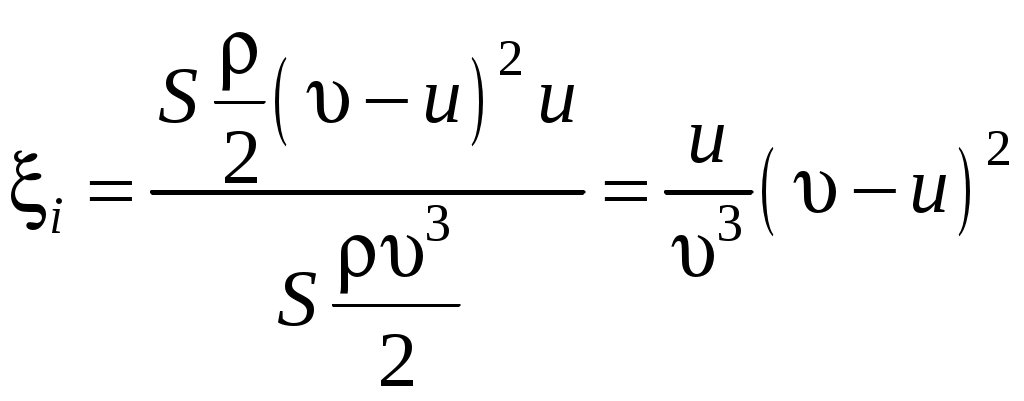 . .
После преобразований получим:
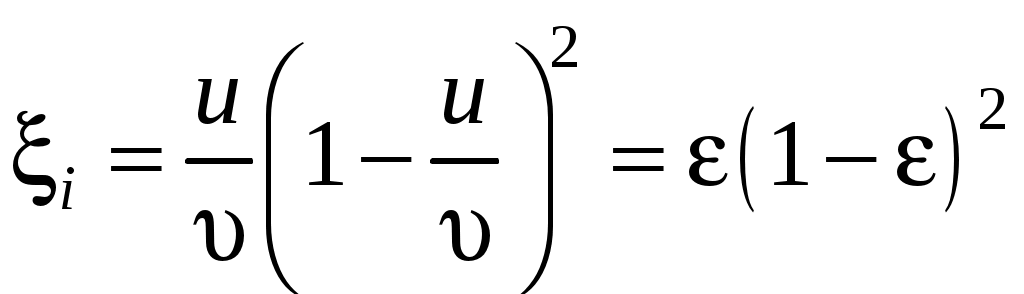 , ,
где 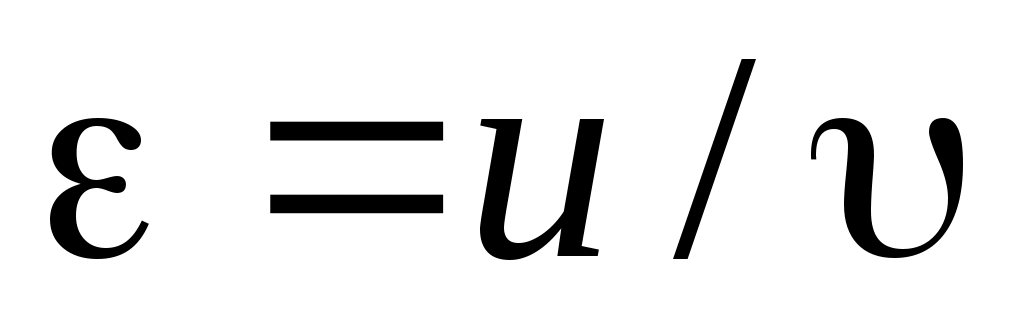 – коэффициент торможения. – коэффициент торможения.
Из уравнения видно, что i зависит от скорости перемещения поверхности в направлении ветра. При некотором значении скорости uкоэффициент получает максимальное значение. В самом деле, если скорость перемещения поверхности равна нулю u = 0, то работа ветра также равна нулю. Если =u, т.е. поверхность перемещается со скоростью ветра, работа также будет равна нулю, так как нет силы сопротивления, за счёт которой совершается работа. Отсюда следует, что значение скорости uзаключено в пределах между u= 0 и u =.
Определим значение , при котором ξiбудет иметь максимальную величину. Для этого возьмём первую производную и приравняем её нулю.
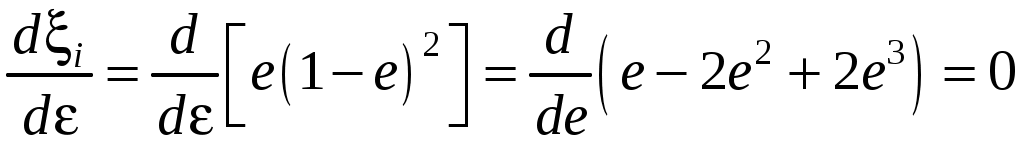
или
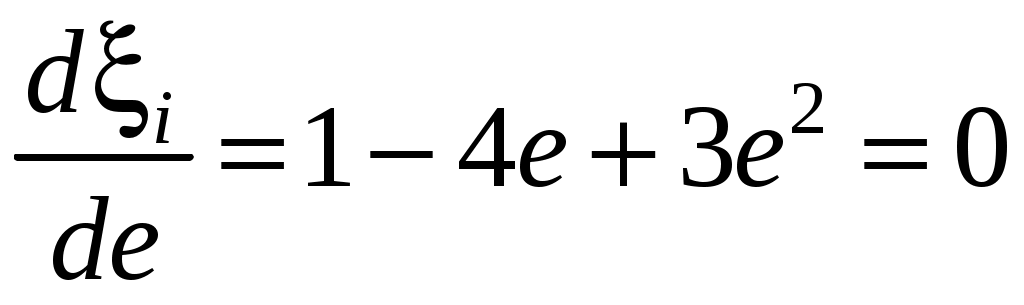 . .
Решая это равенство, находим, что ξi принимает максимальное значение, когда e = 1/3 при этом ξimax= 0,149. Следовательно, максимальный коэффициент использования энергии ветра при работе поверхности силой сопротивления не может быть больше 0,149.
5.5. Теория идеального лопастного ветроколеса
Идеальным лопастным ветроколесом называют ветроколесо, у которого:
1) ось вращения параллельна скорости ветра;
2) бесконечно большое число лопастей очень малой ширины;
3) профильное сопротивление лопастей равно нулю, и циркуляция вдоль лопасти постоянна;
4) потерянная скорость воздушного потока на ветроколесе постоянна по всей ометаемой поверхности ветряка;
5) угловая скорость стремится к бесконечности.
Теорию идеального ветряка впервые разработал в 1914 г. В.П. Ветчинкин на основе теории идеального гребного винта. В этой работе он установил понятие коэффициента использования энергии ветра идеальным ветряком. В 1920 г. проф. Н.Е. Жуковский изложил теорию «Ветряной мельницы», где сделал вывод коэффициента использования энергии ветра идеальным ветряком. Теория идеального ветряка проф. Н.Е. Жуковского носит название классической теории.
Рассмотрим равномерный поток ветра, набегающий на идеальное ветроколесо со скоростью в сечении AA′ (рис. 5.4). В сечении BB′ на ветроколесе скорость будет 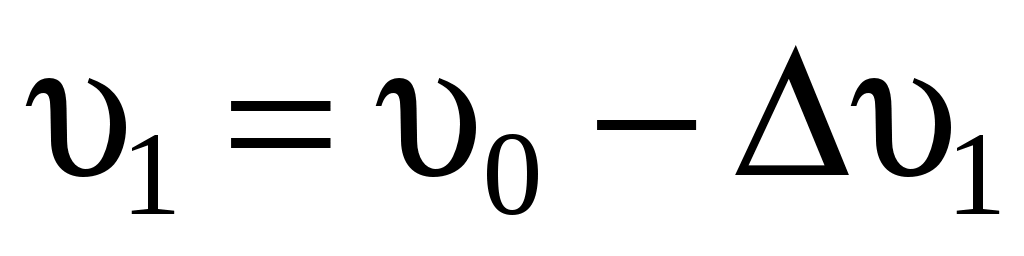 , а на некотором расстоянии позади ветряка в сечении CC′ скорость будет , а на некотором расстоянии позади ветряка в сечении CC′ скорость будет 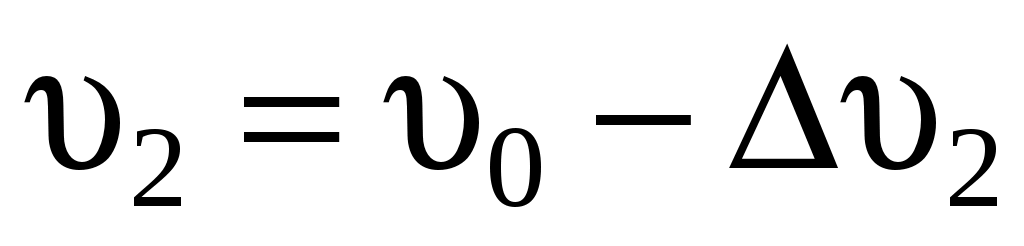 . .
При этом вращающееся ветроколесо создаст подпор, вследствие чего скорость потока, по мере приближения к ветряку и некоторое время за ветряком, падает, как показано кривой 1 на рис. 5.4. Вместе с этим давление воздуха p , по мере приближения к ветряку, повышается (кривая 2), и при прохождении через ометаемую поверхность оно резко падает. За ветряком образуется некоторое разрежение p0 – p2, которое, по мере удаления от ветряка, ассимптотически приближается к нулю, т. е. восстанавливается нормальное давление.
Через ометаемую поверхность Sветроколеса протекает воздух с массовым расходом G:
G= ρS1.
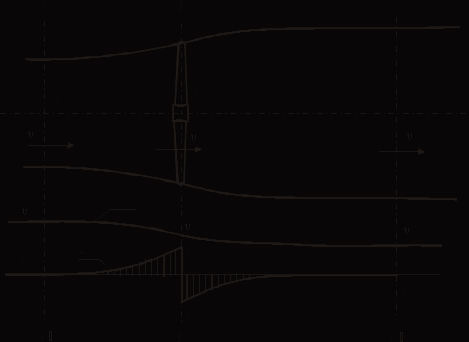
Рис. 5.4. Характеристика воздушного потока, протекающего через ветроколесо
Кинетическая энергия ветра перед ветряком равна 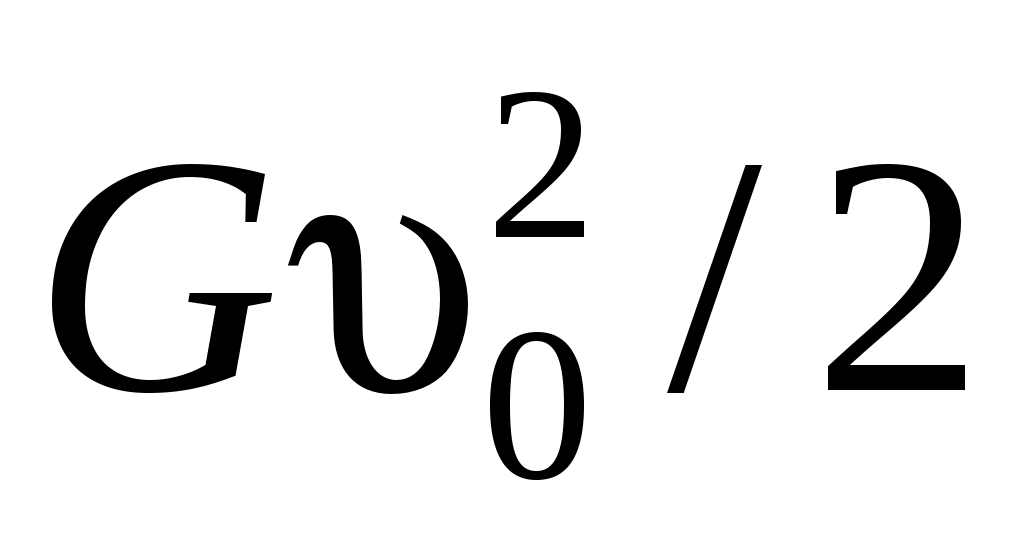 , а за ветряком , а за ветряком 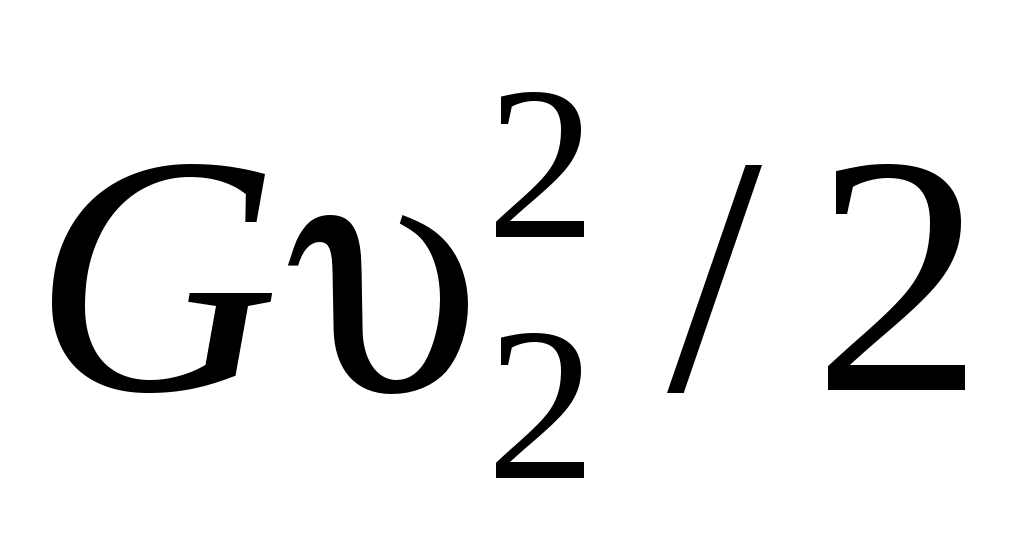 . Разность этих энергий затрачена на ветроколесе и, в случае отсутствия потерь, может быть определена как полезная мощность: . Разность этих энергий затрачена на ветроколесе и, в случае отсутствия потерь, может быть определена как полезная мощность:
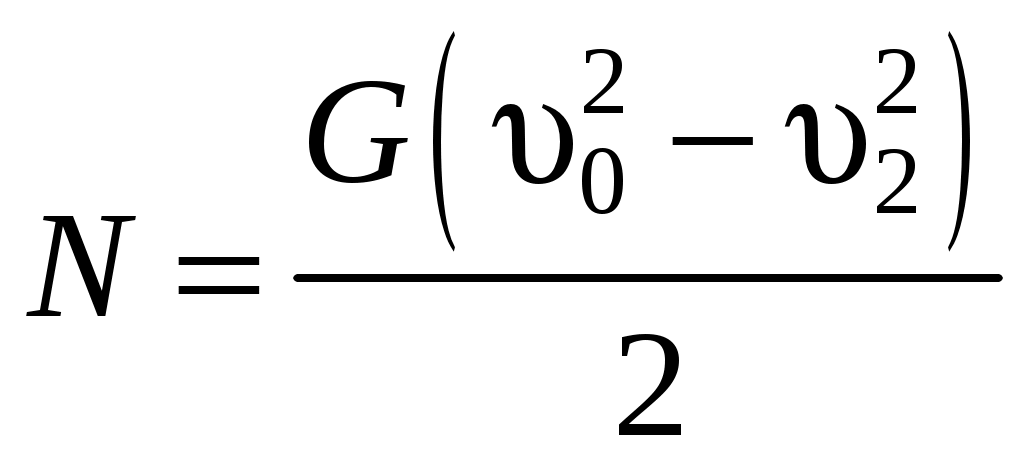 . .
Мощность, воспринятую ветроколесом, можно выразить как произведение из силы давления ветра Fна скорость в плоскости ветряка
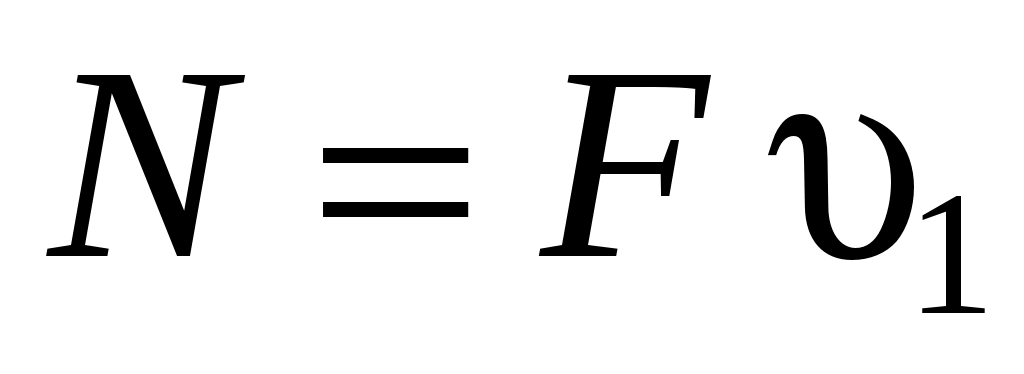 . .
Силу лобового давления Fможно определить из уравнения приращения количества движения струи, проходящей через ометаемую поверхность, т. е.:
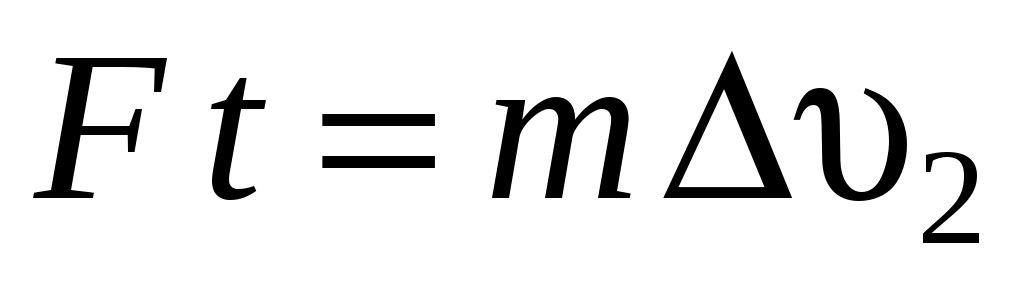 . .
Тогда
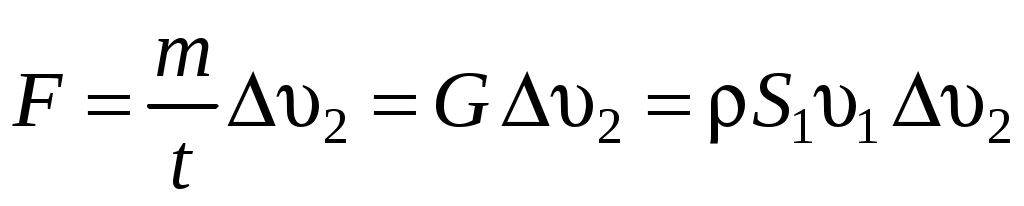 . .
Подставляя значение силы Fв уравнение мощности, получим
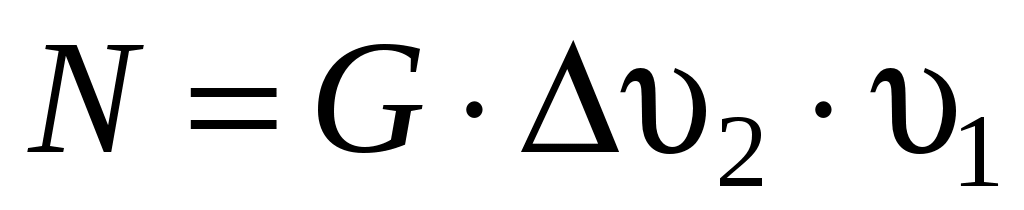
Приравняв оба уравнения для мощности ветроколеса находим, что:
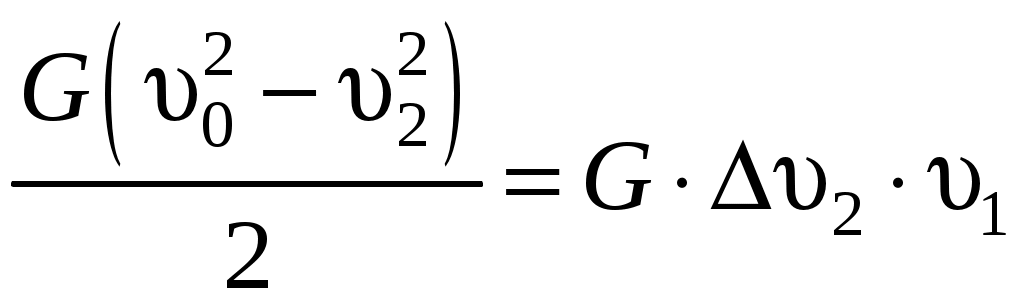
откуда:
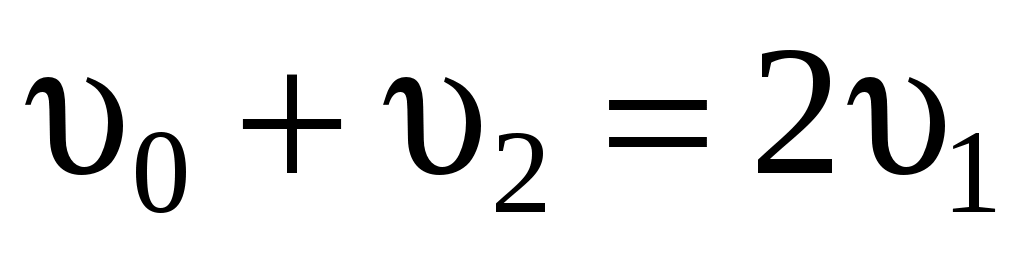 , ,
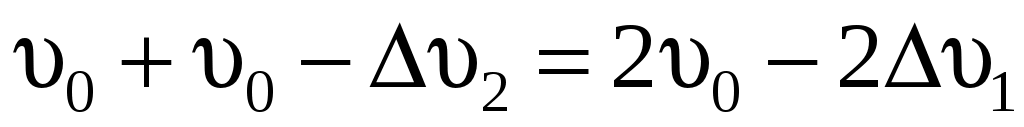 , ,
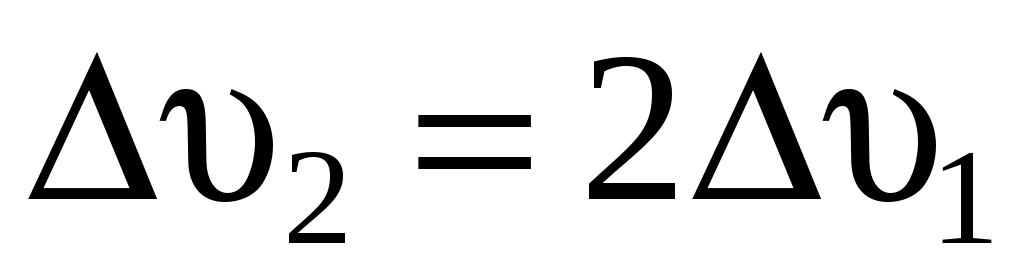 . .
Это равенство показывает, что потеря скорости воздушного потока происходит не только в сечении ветроколеса, но также и на некотором расстоянии за ветряком, причём полная потеря скорости в два раза больше потери на ветроколесе.
Взяв отношение мощности, воспринятой идеальным ветроколесом к энергии ветра, которая протекала бы через сечение, равное ометаемой поверхности ветряка, получим идеальный коэффициент использования энергии ветра ξi
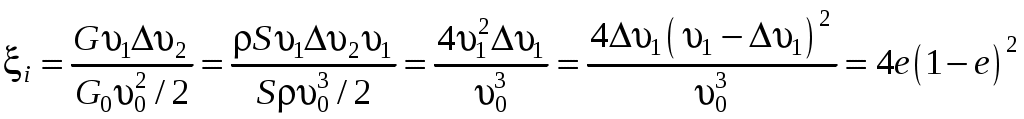 , ,
где 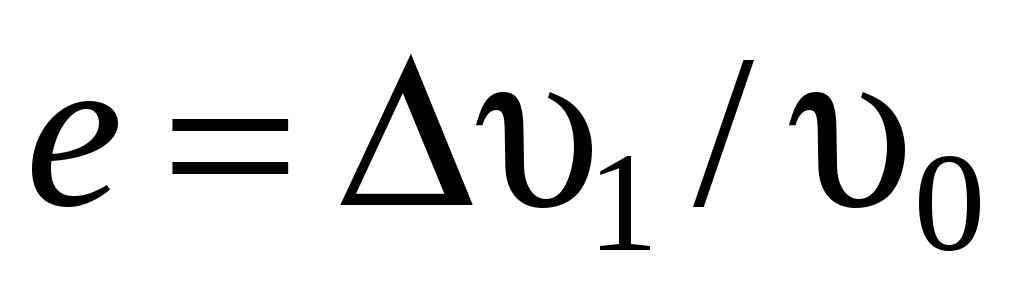 – коэффициент торможения. – коэффициент торможения.
Определим значение e, при котором ξiбудет иметь максимальную величину. Для этого возьмём первую производную и приравняем её нулю.
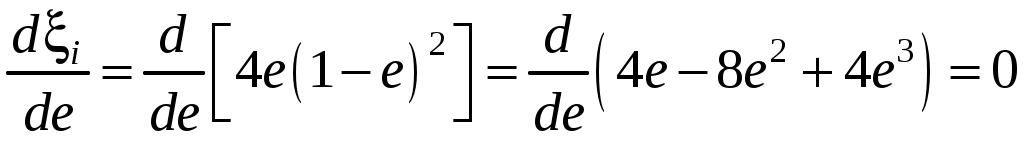
или
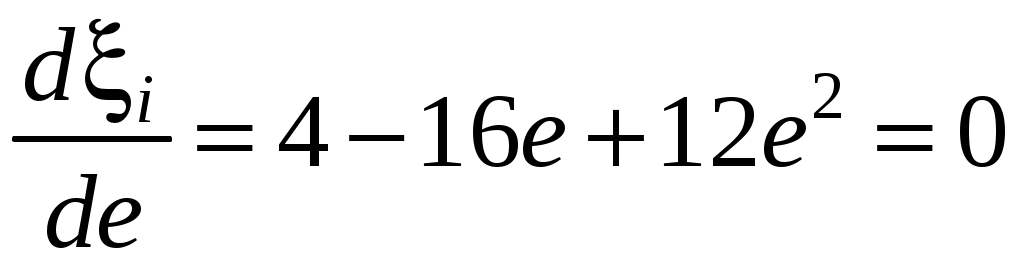 . .
Решая это равенство, находим, что ξi принимает максимальное значение, когда e = 1/3 при этом ξi = 0,593, а
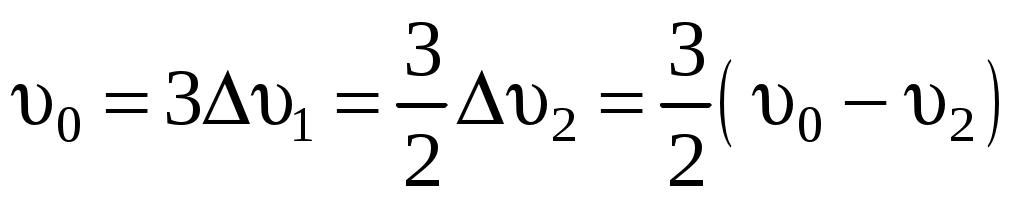 . .
Тогда
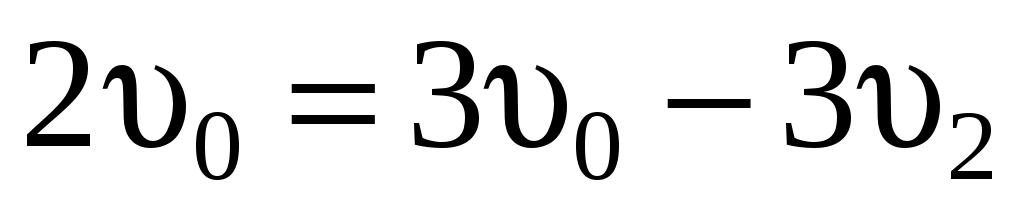 , ,
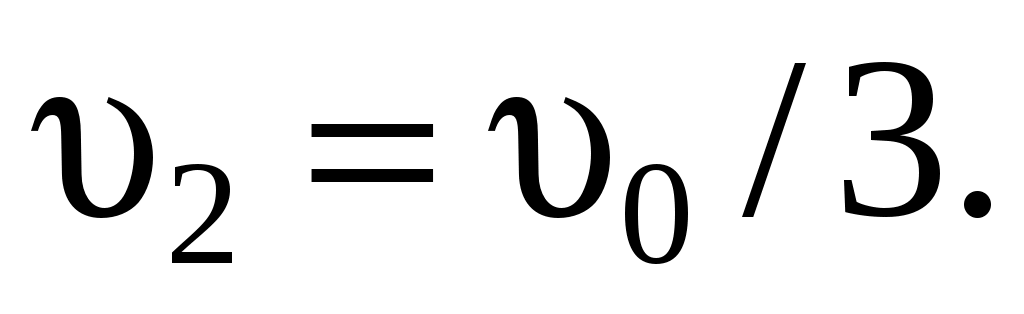
Таким образом, из классической теории идеального ветряка вытекают следующие основные положения:
1. Максимальный коэффициент использования энергии ветра идеального ветроколеса равен ξi = 0,593.
2. При этом скорость ветра за ветроколесом будет в три раза меньше скорости ветра перед ветроколесом.
Наиболее полно, с точки зрения практического применения, теория идеального ветряка изложена проф. Г.X. Сабининым, согласно которой коэффициент использования энергия ветра идеальным ветряком равен 0,687.
Отличие этой теории от прежних теорий заключается в том, что при определении осевой силы давления потока на ветроколесо импульс сил подсчитывается по вихревому соленоиду в том месте, где он принял уже установившуюся цилиндрическую форму, а не в момент его образования, как принималось прежними теориями. Так как соленоид в цилиндрической части имеет площадь сечения большую, чем площадь, ометаемая ветроколесом, то осевая сила и коэффициент использования энергии ветра, по теории Г.X. Сабинина, получаются несколько большими:
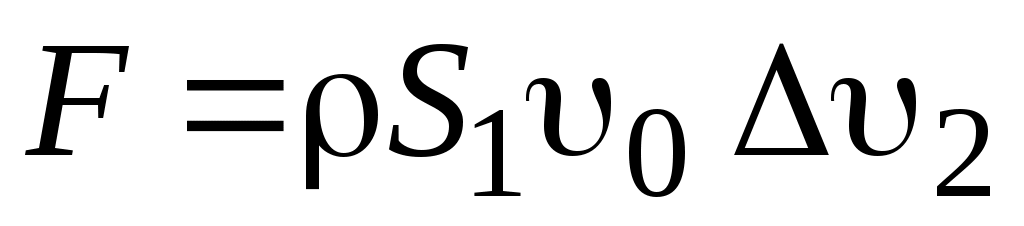 , , 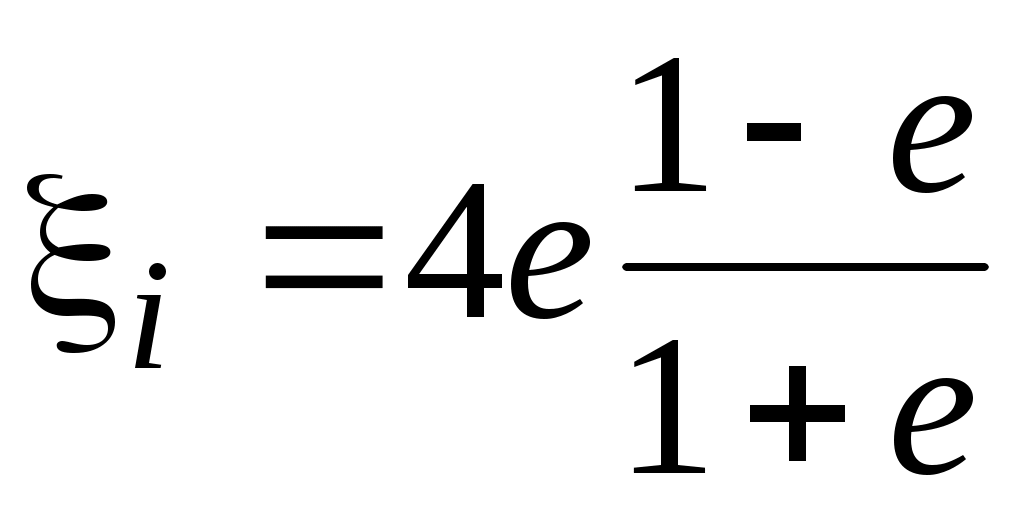 . .
5.6. Работа ветрового колеса крыльчатого ветродвигателя
Крыльчатые ветроколеса работают за счёт косого удара при движении лопастей перпендикулярно к направлению скорости ветра в противоположность к прямому удару, рассмотренному в предыдущем случае. Устройство такого колеса показано на рис. 5.5.
На горизонтальном валу закреплены крылья, число которых у современных ветродвигателей бывает от 2 и больше. Крыло ветроколеса состоит из маха 1 и лопасти 2, закрепляемой на махе так, что она образует с плоскостью вращения некоторый угол . Этот угол называют углом установки лопасти (рис. 5.5). При этом на её элементы набегает воздушный поток с относительной скоростью w под углом , который называют углом атаки, и действует с силой F. Углы и в значительной мере определяют эффективность крыльев. Силу Fраскладывают на силы Fxи Fy(рис. 5.5). Силы Fxпроизводят давление в направлении ветра, которое называется лобовым давлением. Силы Fyдействуют в плоскости вращения ветроколеса и создают крутящий момент.
Максимальные силы, приводящие колесо во вращение, получаются при некотором значении угла атаки , т. е. угла наклона относительного потока к поверхности лопасти. Ввиду того, что окружная скорость по длине крыла не одинакова, а возрастает по мере удаления его элементов от оси вращения ветроколеса, относительная скорость w набегания потока на лопасть также возрастает. Вместе с этим убывает угол атаки , и при некоторой окружной скорости 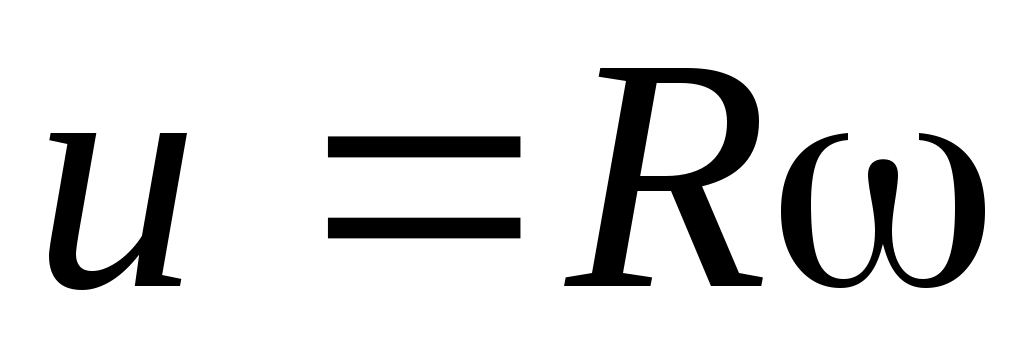 , где угловая скорость, этот угол станет отрицательным (рис. 5.5). Следовательно, не все элементы крыла будут иметь максимальную подъёмную силу. , где угловая скорость, этот угол станет отрицательным (рис. 5.5). Следовательно, не все элементы крыла будут иметь максимальную подъёмную силу.
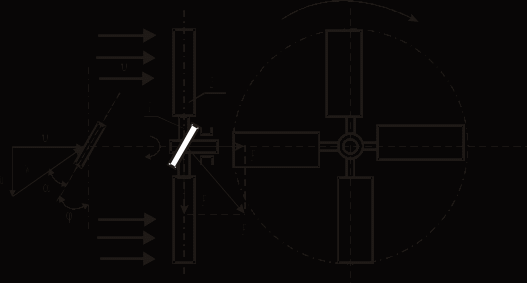
Рис. 5.5. Схема действия сил воздушного потока
на элемент лопасти крыльчатого ветроколеса и план скоростей потока и лопасти
Если мы будем уменьшать угол каждого элемента лопасти по мере удаления его от оси вращения так, чтобы наивыгоднейший угол атаки примерно сохранялся постоянным, то мы получим условие, при котором приблизительно все элементы лопасти будут работать со своей максимальной подъёмной силой. Лопасть с переменным углом установки имеет форму винтовой поверхности.
Правильные углы установки лопасти при хорошем аэродинамическом качестве профиля, а также ширине, соответствующей заданной быстроходности, обеспечивают высокий коэффициент использования энергии ветра (до 0,46).
Аэродинамические потери (около 10–12%) в ветроколесах разделяются на четыре группы:
Концевые потери, происходящие за счет образования вихрей, сходящих с концов лопастей.
Профильные потери, которые вызываются трением струи воздуха о поверхность крыла и зависят только от профиля лопастей.
Потери на кручение струи за ветряком равной кинетической энергии тангенциальных скоростей уходящей струи.
Потери, происходящие вследствие неполного использования всей ометаемой площади.
|
 Скачать 6.34 Mb.
Скачать 6.34 Mb.