Курс лекций по электронике. Курс лекций Курс лекций 1 Введение 4 Полупроводниковые диоды 7

• Название: Курс лекций Курс лекций 1 Введение 4 Полупроводниковые диоды 7
• Анкор: Курс лекций по электронике.doc
• Дата: 16.05.2017
• Размер: 5.23 Mb.
• Имя файла: Курс лекций по электронике.doc
• Тип: Курс лекций; #7720
• страница: 21 из 27

Основные параметры логических элементов

1. Напряжение питания Uпит=+5В+(510)%.

2. Быстродействие.

Характеризуется временем переключения(изменение состояния на противоположное), составляет 5...50 нс.

3. Помехоустойчивость (по входу).

Определяется тем уровнем помех на полезном сигнале, который не приводит к ложному изменению состояния элемента. У большинства ТТЛ -элементов порогом срабатывания их является напряжение Uпор=1,4В, т.е. напряжение от 0 до 1,4В воспринимается как 0, а 1,4В и больше воспринимается как 1.

4. Потребляемая мощность.

5. Нагрузочная способность (по выходу).

Составляет несколько миллиампер.

6. Выходные параметры ТТЛ:

Логической 1 соответствует Uвых2,4В, логическому 0 соответствует Uвых0,4В.

6.6. Синтез комбинационных логических схем

Комбинационные схемы - это схемы, которые не содержат элементов

памяти и элементов выдержки времени.

Последовательность синтеза следующая:

1. Задаётся словесный алгоритм работы схемы.

2. Составляется таблицы истинности.

3. Записывается исходная логическая функция и выполняется её минимиза-ция.

4. Выполняется реализация полученной логической функции на логических элементах.

Пример: требуется построить логическую схему голосования на 3 вхо-

да: cигнал на выходе схемы равен 1, когда большинство входных сигналов равно 1.

Составляем таблицу истинности: таблица истинности - это табличная запись алгоритма. Обозначим входные переменные: x1,x2,x3. В таблице истинности для входных переменных должны быть записаны все возможные комбинации. Число строк в такой таблице равно 2 в степени n, где n -количество входных переменных. Выходная логическая функция  записывается по словесному алгоритму (рис.110). Когда две или три входных пере-

менных равны 1, выходная функция тоже равна 1.

По таблице истинности может быть записано логическое выражение. Форма записи по таблице истинности называется совершенно нормальной формой. Существует две формы записи: дизъюнктивная совершенно нормальная форма - сокращенно ДСНФ, конъюнктивная совершенно нормальная форма - КСНФ. Обычно запись ведётся в дизъюнктивной форме. В этой форме записи принимаются во внимание строки, в которых логическая функция принимает значение 1. Произведения переменных этих строк складываются логически. ДСНФ для нашего примера:



Можно принимать во внимание строки с нулевым значением функции, только при этом каждая строка - это сумма переменных строки, а между собой суммы переменных соединяются произведением. Функция называется КСНФ.

Дальше выполняется следующий этап синтеза - минимизация, т.к. реализация логической функции по ДСНФ является достаточно сложной ввиду большого размера выражения для f. Цель минимизации - упростить выражение до такого вида, которое далее бы не упрощалось. В результате получается, так называемая, тупиковая форма.

6.6.1. Методы минимизации

Минимизация может быть выполнена несколькими способами.

1. На основе законов алгебры логики.

Недостаток метода - сложно выбрать из законов подходящий закон для очередного упрощения, трудно наметить путь преобразования, нельзя гарантировать, что полученная упрощенная форма является тупиковой.

2. Метод карт Карно.

Применяется при числе переменных n<5...6.

3. Метод Квайна и его модификации. Является табличным, не имеет ограничений по количеству переменных. Сложный, но хорошо поддаётся

алгоритмизации и исполнению на ЦВМ.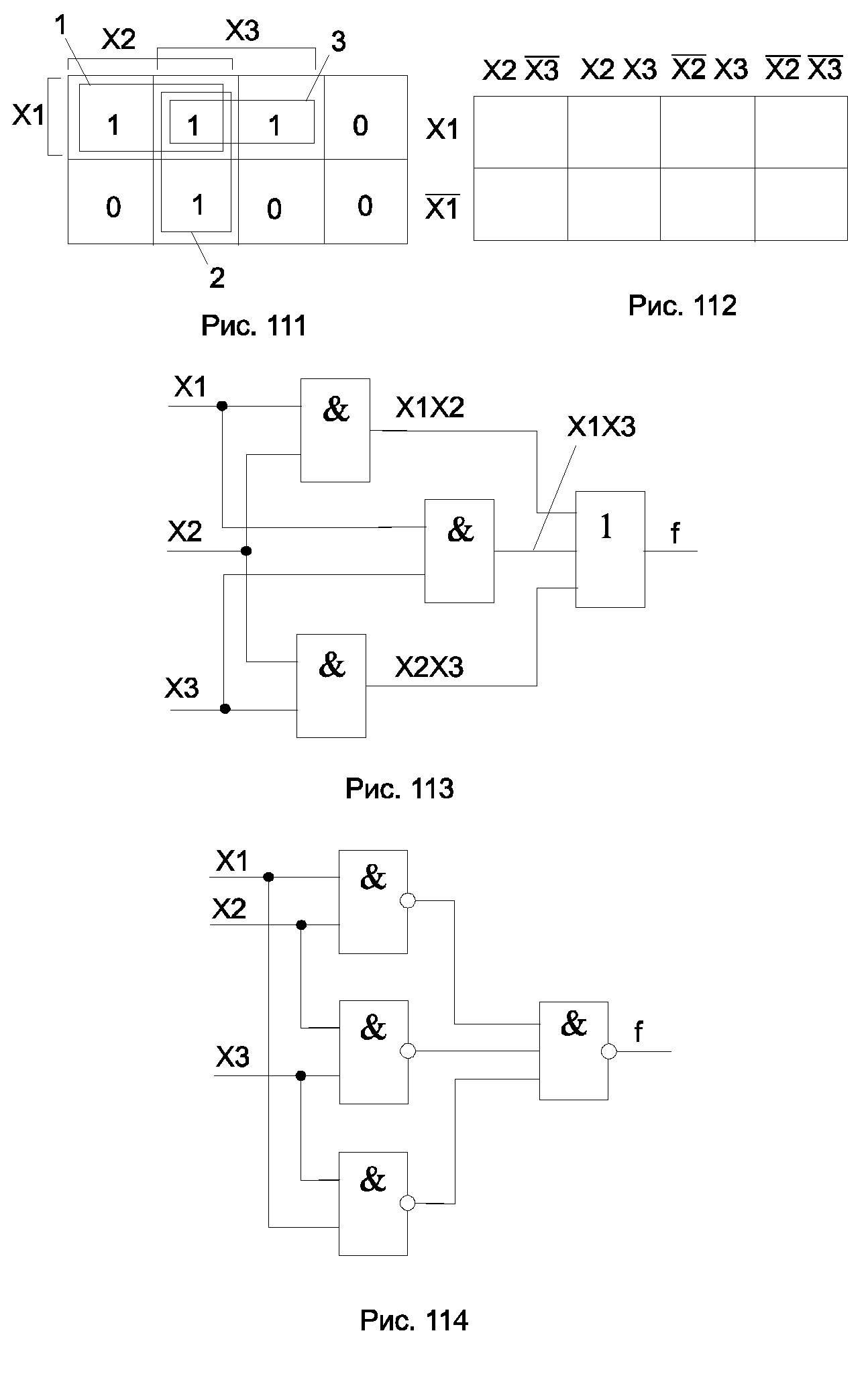

Минимизация с помощью карт Карно

Карта Карно представляет собой прямоугольную таблицу, в которой число клеток равно 2 в степени n. Карта заполняется на основе таблицы истинности или записи логической функции в ДСНФ.

Для приведенного выше примера таблица истинности имеет вид, представленный на рис. 111. Внутри карты Карно записываются значения

логической функции. Значения входных переменных записываются по кра-

ям карты. Каждая входная переменная делит поле карты пополам. Для од-

ной половинки поля значения входных переменных равны 1, для другой - 0. При расстановке переменных необходимо соблюдать следующее правило:

соседние столбцы и строки должны различаться только одной переменной. Значение входной переменной, равное 1, принято охватывать скобочкой.

Там, где нет скобочки, значение переменной равно 0. Возможно другое обозначение переменной по краю Карты (рис. 112).

Далее единицы в карте Карно объединяются контурами. Правила нанесения контуров:

1. Каждый контур должен быть прямоугольным.

2. Количество клеток внутри контура должно быть равным 2 в степени n,

где n=1,2,3,...

3. Одни и те же клетки с единицами могут входить в несколько контуров.

4. Размеры контуров должны быть как можно большими, а число контуров

как можно меньше.

Запись минимизированного выражения по карте Карно с нанесенны-

ми контурами выполняется по следующим правилам:

1. Количество слагаемых в дизъюнктивной форме равно количеству конту-

ров.

2. Из конъюнкции переменных исчезают те переменные, границы изменения которых пересекаются контуром.

Для рассматриваемого примера:

В этом выражении x1x2 записано из первого контура, x2x3 - из второго контура, x1x3 - из третьего контура.

Реализация по этому выражению имеет вид, представленный на рис.

113. Реализация требует 2 корпуса микросхем.

Для уменьшения количества корпусов преобразуют полученную логическую функцию по законам Моргана и записывают её в базисе И-НЕ

или в базисе ИЛИ-НЕ. Применение законов Моргана позволяет избавить-

ся от “+” в логической функции или от произведений. Один из законов Моргана имеет вид:

Изменим запись закона

Запись справедлива для любого количества элементов. Под a и b можно понимать логические выражения. Применим формулу для нашего выраже-

ния:




Реализация по данному выражению показана на рис. 114. Реализация требу-

ет два корпуса микросхем.