ЖБК. Курс лекций. Курс лекций по дисциплине Железобетонные конструкции для специальностей Архитектура иПромышленное и гражданское строительство
 Скачать 1.89 Mb.
|
|
7.4.2. Расчет прочности по нормальным сечениям элементов прямоугольного и таврового профилей Элементы прямоугольного профиля с одиночной арматурой (рис. 27). Высоту сжатой зоны х определяют из уравнения равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента: 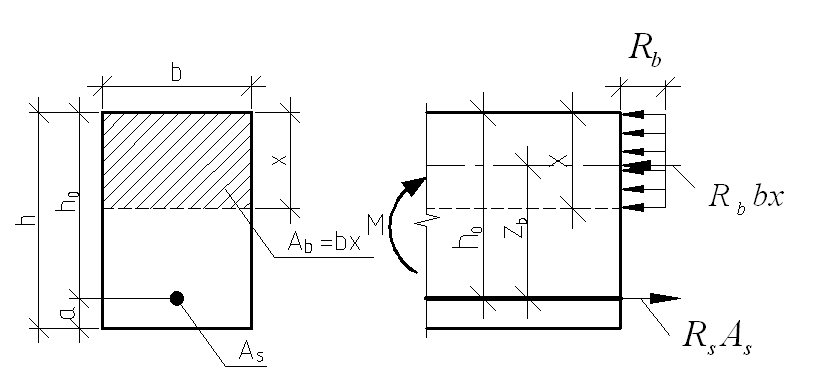   . Рис. 27. Прямоугольное сечение с одиночной арматурой и схема усилий. Условие прочности по сжатой зоне:  . (1)Условие прочности по растянутой арматуре:  . (2)Данные формулы применяют при условии  .В практике для расчета прямоугольных сечений с одиночной арматурой используют табличный метод. С этой целью формулы (1) и (2) преобразуют следующим образом:        ,где  ;  ;  .  . (3)   . . (4)Для коэффициентов  ,  и  составлена таблица (приложение 1). По формуле (3) определяют , затем по таблице в зависимости от находят соответствующие и . Проверяют условие . Если условие выполняется, находят требуемое количество арматуры по формуле (4). Элементы прямоугольного профиля с двойной арматурой (рис. 28). Если при расчете прочности элемента прямоугольного профиля с одиночной арматурой оказалось, что 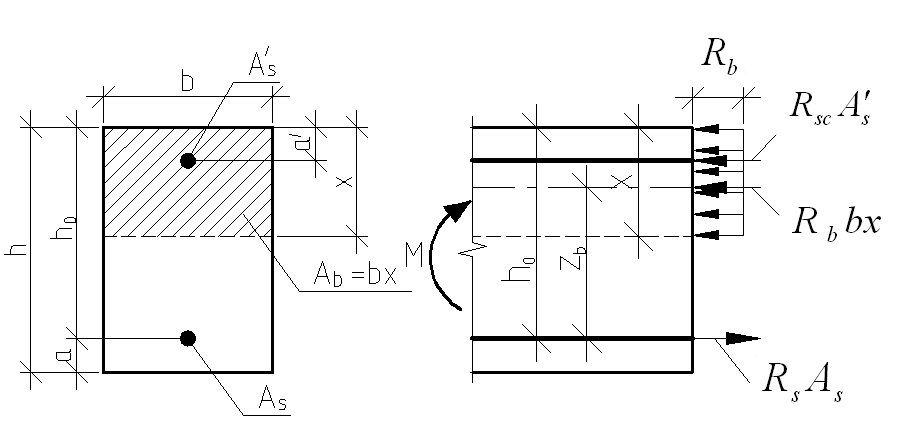 , значит прочности сжатой зоны бетона недостаточно и арматура в этой зоне требуется по расчету.  Рис. 28. Прямоугольное сечение с двойной арматурой и схема усилий. Условие прочности по сжатой зоне изгибаемого элемента, армированного двойной арматурой:  . (5)Из уравнения равенства нулю суммы проекций всех нормальных усилии на продольную ось элемента:    .Если при расчете прочности элемента прямоугольного профиля с одиночной арматурой оказалось, что , принимают  , затем по таблице находят соответствующее значение  . Формулу (5) преобразуем следующим образом: ; . (6)Требуемую площадь сжатой арматуры A’sможно определить из формулы (6): 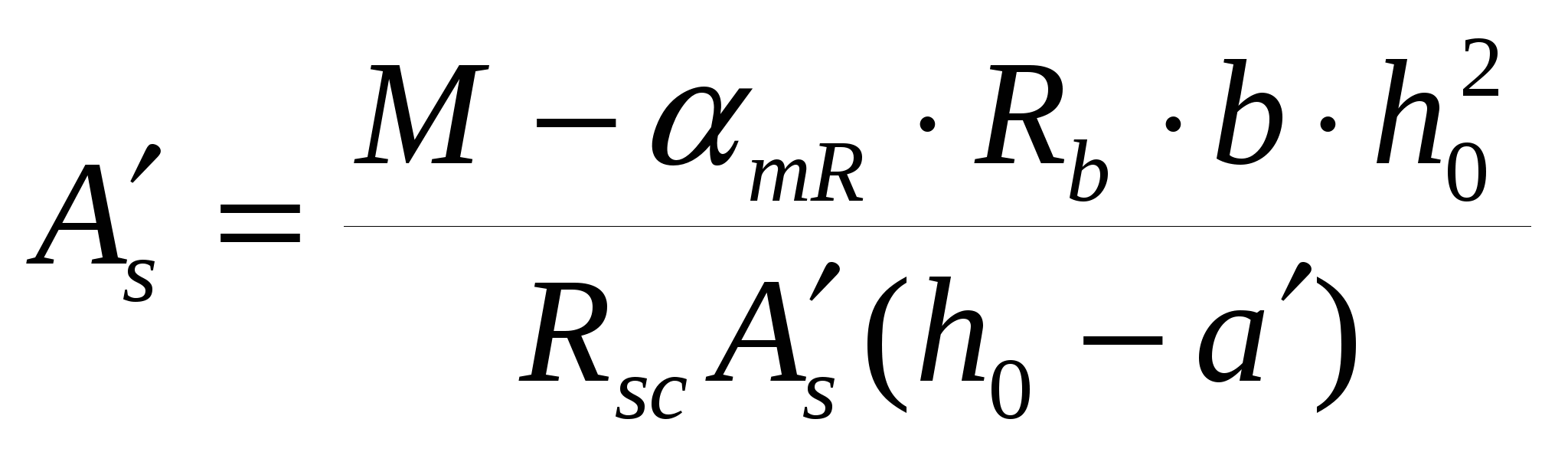 .Из уравнения равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента находят требуемую площадь растянутой арматуры:    .Элементы таврового профиля. Расчеты прочности некоторых железобетонных конструкций (многопустотные и ребристые плиты перекрытий) сводятся в итоге к расчету таврового сечения (рис. 29). Тавровое сечение образуется из полки и ребра. Основное преимущество таврового сечения перед прямоугольным – это отсутствие «лишнего» бетона в растянутой зоне, поэтому в сравнении с прямоугольным тавровое сечение значительно выгоднее, т.к. при одной и той же несущей способности (бетон растянутой зоны не влияет на несущую способность) расход бетона значительно меньше. При большой ширине полок участки свесов, более удаленные от ребра, напряжены меньше. Поэтому в расчеты вводят только часть полки, участвующей в работе – не более половины расстояния в свету между ребрами c и не более 1/6 пролета рассматриваемого элемента (рис. 30, а). При консольных свесах полок (рис. 30, б) вводимая в расчет ширина свеса должна составлять: - при  . . . . . . . . . . . . . . . . . . . . . не более 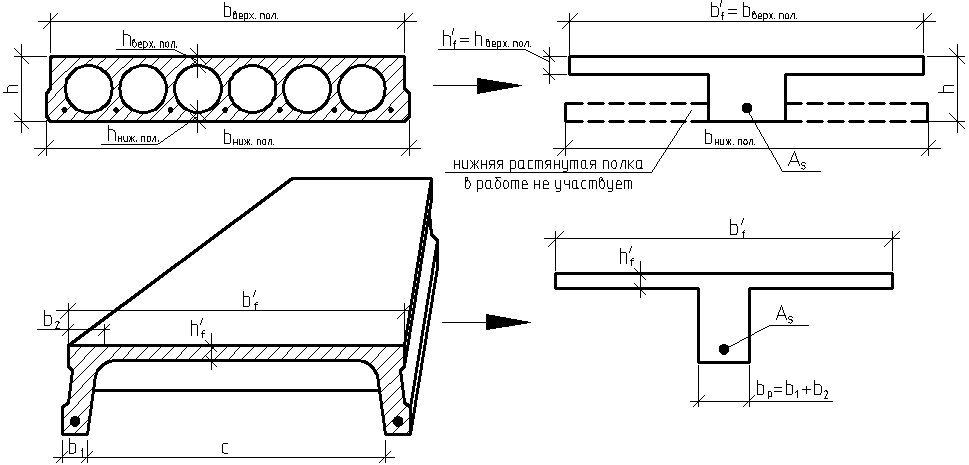6 ;- при  . . . . . . . . . . . . . . не более 3;- при  . . . . . . . . . . . . . . . . . . . свесы полок в расчете не учитывают. а  )б) Рис. 29. Плиты перекрытий и их расчетные сечения: а – многопустотная плита; б – ребристая плита. 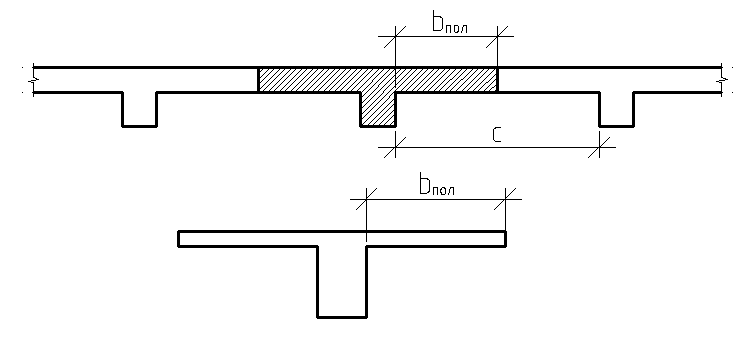 а) б) Рис. 30. Участки свесов тавровых сечений, вводимые в расчеты: а – в составе монолитного перекрытия; б – при консольных свесах полок. Два расчетных случая в элементах таврового профиля Расчетный случай зависит от положения границы сжатой зоны бетона. 1 случай. Граница сжатой зоны проходит в полке  . В этом случае тавровое сечение рассчитывают как прямоугольное с размерами  (рис. 31), поскольку бетон в растянутой зоне на несущую способность не влияет.  Рис. 31. 1 случай положения границы сжатой зоны бетона в элементах таврового профиля. 2 случай. Граница сжатой зоны находится в ребре (рис. 32). Расчет проводят по формулам таврового профиля. 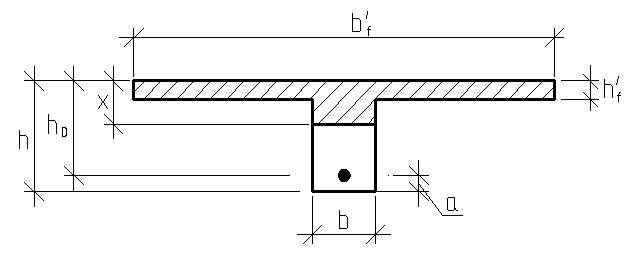 Рис. 32. 2 случай положения границы сжатой зоны бетона в элементах таврового профиля. Определение расчетного случая При решении прямой задачи, т.е. когда необходимо определить требуемое количество растянутой арматуры, предполагают, что нижняя граница сжатой зоны проходит по нижней грани полки (рис. 33), определяют величину несущей способности таврового сечения на изгиб и сравнивают с величиной изгибающего момента от действия внешних нагрузок. 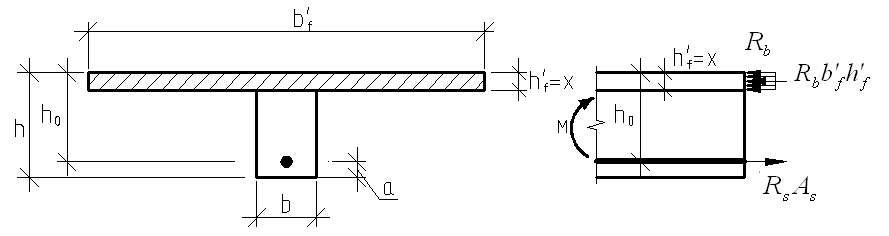 - граница сжатой зоны находится в полке; - граница сжатой зоны находится в ребре.  Рис. 33. К определению расчетного случая в элементах таврового профиля. При решении обратной задачи, т.е. когда требуется проверить несущую способность элемента при известном количестве арматуры в элементе, граница сжатой зоны определяется из уравнения равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента:  ;  , при расчетным сечением является прямоугольник, а при  - сечение таврового профиля.Расчет арматуры растянутой зоны в элементах таврового профиля (рис. 34). 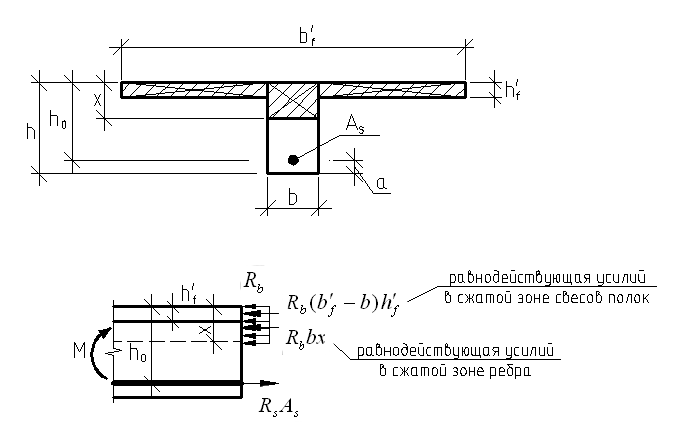 Рис. 34. К расчету растянутой арматуры в элементах таврового профиля. Условие прочности по сжатой зоне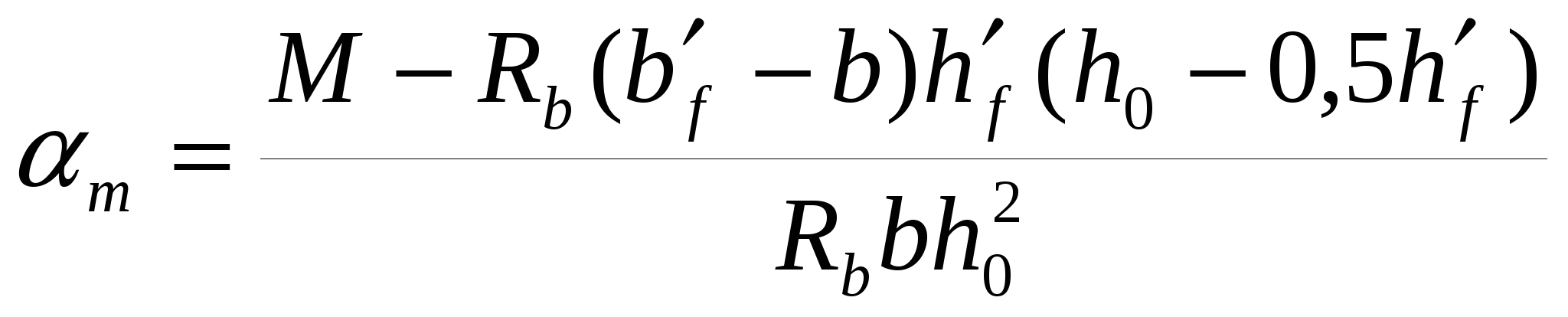:  (7)Заменяя  на  из условия прочности (7) определяют значение  : , затем по таблице находят соответствующее значение . Проверяют условие . Из уравнения равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента:  определяют неизвестное количество требуемой растянутой арматуры:   .Если , необходима арматура в сжатой зоне. Расчет арматуры сжатой зоны в элементах таврового профиля (рис. 35). 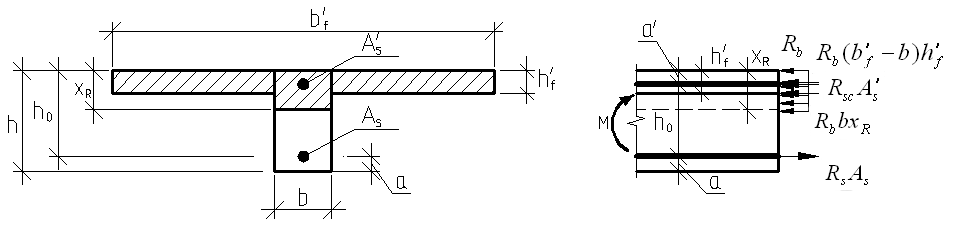 Рис. 35. К расчету сжатой арматуры в элементах таврового профиля. Принимаем , т.е. бетон сжатой зоны работает до предела. Условие прочности:  . (8)Используя 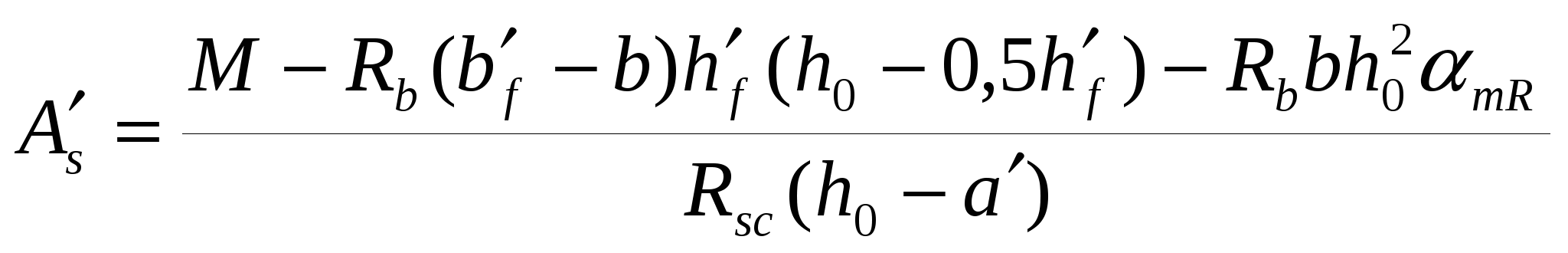 из условия прочности (8) определяют неизвестное количество требуемой сжатой арматуры: .Из уравнения равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента:  определяют неизвестное количество требуемой растянутой арматуры:   .7.4.3. Расчет прочности элементов по наклонным сечениям На приопорных участках под действием поперечной силы и изгибающего момента в сечениях, наклонных к продольной оси элемента, развиваются напряженно-деформированные состояния, как и в нормальных сечениях. Главные растягивающие и главные сжимающие напряжения действуют под углом к оси (рис. 36). 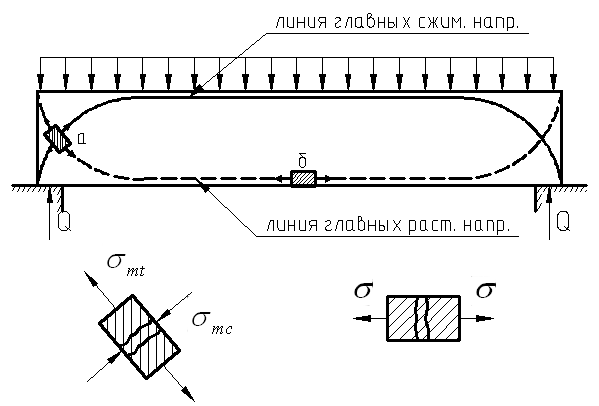 а) б) Рис. 36. Линии главных сжимающих и растягивающих напряжений. Если главные растягивающие напряжения  превысят сопротивление бетона растяжению Rbt, возникают наклонные трещины. Растягивающие усилия в наклонной трещине передаются на арматуру. При дальнейшем увеличении нагрузки наклонные трещины раскрываются, напряжения в арматуре доходят до предела текучести и происходит разрушение элемента вследствие раздробления бетона над вершиной наклонной трещины (рис. 37).  Рис. 37. Схема разрушения элемента по наклонному сечению. Разрушение изгибаемого элемента по наклонному сечению происходит по одному из трех возможных случаев: 1. Раздробление бетона наклонной сжатой полосы между наклонными трещинами (рис. 38). Происходит при малой ширине сечения, когда главные сжимающие напряжения превышают расчетное сопротивление бетона сжатию Rb. Э 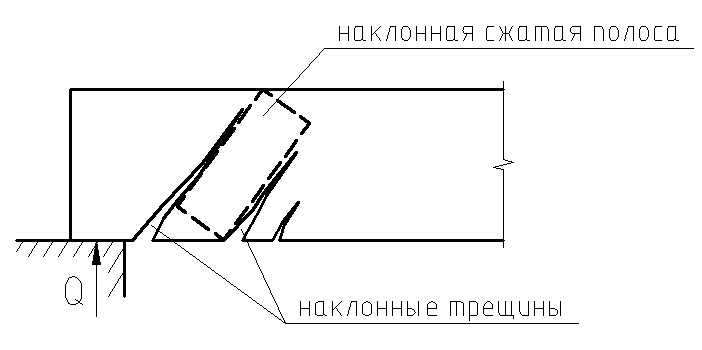 кспериментально установлено, что прочность железобетонных элементов по наклонной полосе между наклонными трещинами обеспечена, если соблюдается условие:Рис. 38. Раздробление бетона наклонной сжатой полосы между наклонными трещинами.  ,где  - коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, определяется по формуле:  , где  ,  ;  - определяется по формуле:  , где β – коэффициент, зависящий от вида бетона; Rb - в МПа. Если условие не соблюдается, необходимо увеличить размеры сечения или повысить класс бетона. 2. Сдвиг по наклонному сечению от действия поперечной силы (рис. 39). 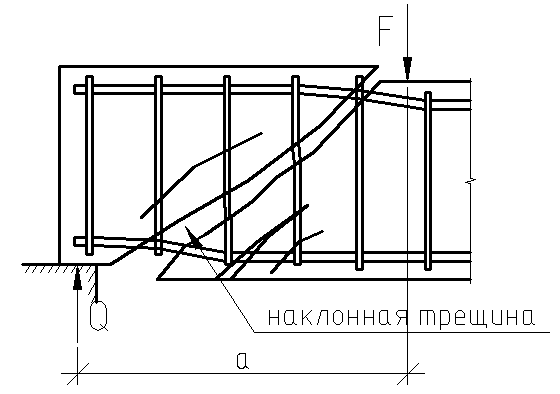 Образование наклонной трещины происходит при  .При разрушении происходит взаимное смещение частей элемента по вертикали. Расчет прочности наклонных сечений на действие поперечной силы производят в обязательном порядке. Е Рис. 39. Сдвиг по наклонному сечению от действия поперечной силы. сли касательные напряжения не достигают максимального значения, наклонные трещины не образуются. Т.е. если  , поперечная арматура ставится конструктивно. При расположении сосредоточенной силы F близко к опоре (a/h≤ 1….1,5) трещиностойкость наклонных сечений увеличивается тем больше, чем ближе сила F к опоре. 3. Излом по наклонному сечению от действия изгибающего момента (рис. 40). П |