Курс лекций. Курс лекций ОЭФ(Кв) 14 (копия). Курс лекций по дисциплине Общая и экспериментальная физика для студентов ВлГУ
 Скачать 7.12 Mb. Скачать 7.12 Mb.
|
|
Лекция 14. Характеристическое рентгеновское излучение. План лекции. Получение характеристического излучения. Практическое применение для изучения структуры вещества. Рентгеновское излучение – ЭМИ, коротковолнового диапазона. 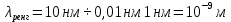 . Впервые в 1912 г. немецкий физик М.Лауэ получил дифракцию рентгеновских лучей на кристаллической решетке. Как отмечено выше (лекция 7), рентгеновские лучи получают в рентгеновских трубках, принципиальная схема устройства которой представлена на рисунке. . Впервые в 1912 г. немецкий физик М.Лауэ получил дифракцию рентгеновских лучей на кристаллической решетке. Как отмечено выше (лекция 7), рентгеновские лучи получают в рентгеновских трубках, принципиальная схема устройства которой представлена на рисунке.П 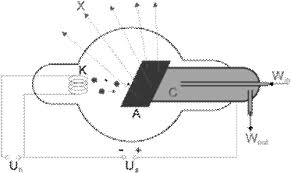 роцессы, происходящие в рентгеновских трубках: роцессы, происходящие в рентгеновских трубках:термоэлектронная эмиссия (катод разогревается, с поверхности катода вылетают электроны); ускорение электронов электрическим полем; электроны долетают до анода и тормозятся – торможение электронов на аноде. С 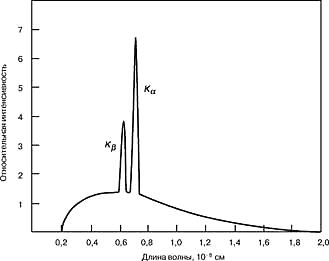 увеличением напряжения между катодом и анодом можно получить условия, когда электроны обладают настолько большой энергией, что они не затормозятся на поверхности анода, а проникают внутрь атомов вещества анода, доходя до внутренних электронных оболочек (вблизи ядра атома). Тогда, за счет внутриатомных процессов излучение будет иметь линейчатый спектр и на фоне сплошного спектра появляются отдельные пики разной интенсивности. Это линии характеристического рентгеновского излучения (рисунок). увеличением напряжения между катодом и анодом можно получить условия, когда электроны обладают настолько большой энергией, что они не затормозятся на поверхности анода, а проникают внутрь атомов вещества анода, доходя до внутренних электронных оболочек (вблизи ядра атома). Тогда, за счет внутриатомных процессов излучение будет иметь линейчатый спектр и на фоне сплошного спектра появляются отдельные пики разной интенсивности. Это линии характеристического рентгеновского излучения (рисунок).Спектр характеристического излучения линейчатый. Линии объединяются в серии: K- серия, L- серия и т. д.) .Характеристическое рентгеновское излучение объясняется внутриатомными процессами (рисунок).  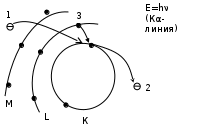   Ze Быстрые электроны, проникая внутрь электронной оболочки атома (1), выбивают электроны, принадлежащие внутренним электронным слоям. Ближайший к ядру электронный слой (К - слой) содержит два электрона. Если один из этих электронов оказывается выбитым за пределы атома (2), то при переходе электрона (3) с вышележащих слоев (L,M) на К-слой и возникает соответствующая линия К-серии (рис.). При переходе электрона с L- слоя на К-слой излучается наиболее интенсивная Кα - линия характеристического рентгеновского спектра. Электроны L -слоя находятся в поле ядра с зарядом Ze, которое ослаблено одним электроном, оставшимся в К-слое. Таким образом, заряд Z1e (эффективный заряд), определяющий электрическое поле в котором находится электрон, переходящий с L -слоя на К-слой, меньше заряда ядра на величину заряда одного электрона: 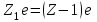 . .Внешние электронные слои можно рассматривать как сферически симметричные, и тогда электрическое поле внутри этих слоев отсутствует. Поэтому для L –>K - перехода, модно воспользоваться сериальной формулой 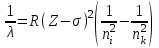 , полученной Мозли в 1913 году, где R - постоянная Ридберга, σ - постоянная экранирования. Для линий К-серии ni = 1, σ =1. В частности, для линии Кα, когда переход электрона в атоме происходит с L-слоя ( nk= 2), получим: , полученной Мозли в 1913 году, где R - постоянная Ридберга, σ - постоянная экранирования. Для линий К-серии ni = 1, σ =1. В частности, для линии Кα, когда переход электрона в атоме происходит с L-слоя ( nk= 2), получим: 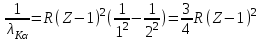 . Тогда энергия излучаемого рентгеновского кванта равна . Тогда энергия излучаемого рентгеновского кванта равна 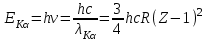 ; ; 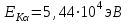 . . Рентгеновские лучи находят широкое применение. Так, например, дифракция рентгеновских лучей на кристаллах, квазикристаллах, наноструктурах применяется в рентгеновском структурном анализе для определения структур атомных, молекулярных и нанокластеров. Самым общим случаем дифракции является дифракция в среде с трехмерным распределением неоднородностей (кристаллах). Так как величины межплоскостных расстояний в кристаллах того же порядка, что и длины волн рентгеновского излучения, то кристаллы являются естественными дифракционными решетками для рентгеновских лучей. По полученной дифракционной картине можно определить строение, атомную структуру кристалла. Метод называется рентгеновским структурным анализом, который применяется . в физике, химии, биологии и технике. Рассмотрим условия , описывающие данное явление. Рассмотрим сначала интерференцию лучей, рассеянных атомами, расположенными вдоль прямой линии. Пусть на атомы 1,2,3,… атомного ряда падает плоская волна монохроматических рентгеновских лучей. Период повторяемости вдоль атомного ряда равен 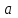 . Выделим лучи, рассеянные под произвольным углом к атомному ряду. Очевидно, условия интерференции рассеянных лучей будут такими же, что и в случае обычной дифракционной решетки. Условие дифракционного максимума интенсивности запишется уравнением: . Выделим лучи, рассеянные под произвольным углом к атомному ряду. Очевидно, условия интерференции рассеянных лучей будут такими же, что и в случае обычной дифракционной решетки. Условие дифракционного максимума интенсивности запишется уравнением: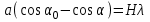 , (1) , (1)где 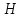 – целое число (порядок дифракции), – целое число (порядок дифракции), 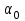 и и 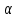 - углы между атомным рядом и лучами, падающими и отклоненными. Дифрагированные лучи образуют систему коаксиальных конусов, общей осью которых является направление атомного ряда. - углы между атомным рядом и лучами, падающими и отклоненными. Дифрагированные лучи образуют систему коаксиальных конусов, общей осью которых является направление атомного ряда. 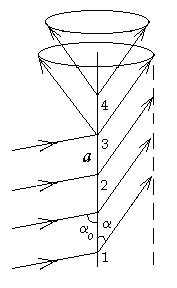 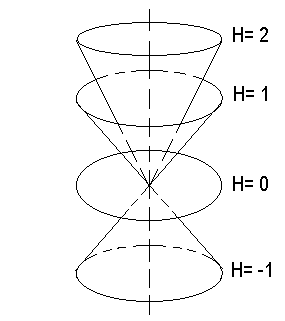 Дифракция на атомном ряде и дифракционные конусы от атомного ряда. Очевидно, что при прохождении рентгеновских лучей через пространственную решетку рассеяние будет происходить лишь в тех направлениях, для которых одновременно будут удовлетворены три уравнения: 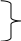 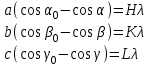 , (2) , (2)где 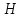 , , 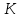 , , 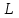 - индексы интерференции, - индексы интерференции, 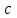 - период повторяемости третьего атомного ряда, - период повторяемости третьего атомного ряда, 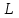 - целое число, - целое число, 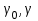 - углы третьего атомного ряда с падающим и отклоненным лучами. Соотношения (2) называются уравнениями Лауэ. - углы третьего атомного ряда с падающим и отклоненным лучами. Соотношения (2) называются уравнениями Лауэ.Значительно более простая и наглядная теория дифракции рентгеновских лучей, приводящая к тем же результатам, что и теория Лауэ, была предложена в 1913 г. русским физиком Вульфом и англичанами Брэггами. Они рассматривали рассеяние рентгеновских лучей кристаллом как их своеобразное отражение от атомных плоскостей, проведенных через узлы кристаллической решетки, с соблюдением равенства углов падения и отражения. 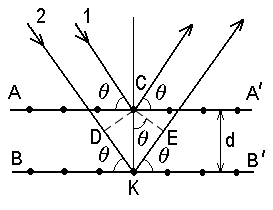 К выводу уравнения Вульфа-Брэгга. На рисунке показаны две соседние атомные плоскости кристалла 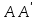 и и 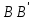 , расстояние между которыми , расстояние между которыми 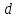 . На плоскости падают рентгеновские лучи с длиной волны . На плоскости падают рентгеновские лучи с длиной волны 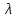 . Разность хода между лучами 1 и 2 равна . Разность хода между лучами 1 и 2 равна 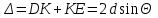 , где , где 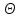 - угол скольжения. Лучи 1 и 2 усилятся в результате интерференции в том случае, когда разность хода - угол скольжения. Лучи 1 и 2 усилятся в результате интерференции в том случае, когда разность хода 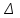 = =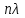 . Окончательно получаем: . Окончательно получаем: 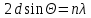 , (3) , (3)где 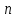 =1,2,… - порядок дифракционного максимума. Соотношение (3), называемое уравнением Вульфа-Брэгга, лежит в основе рентгеноструктурного анализа кристаллов. Зная =1,2,… - порядок дифракционного максимума. Соотношение (3), называемое уравнением Вульфа-Брэгга, лежит в основе рентгеноструктурного анализа кристаллов. Зная 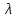 , можно исследовать строение кристаллических решеток и определять межплоскостные расстояния , можно исследовать строение кристаллических решеток и определять межплоскостные расстояния 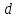 . Знание атомной структуры важно, так как она определяет свойства соединений. Так, например в международном банке структурных данных только для органических соединений содержится информация о структурах более 400 000 тысяч. . Знание атомной структуры важно, так как она определяет свойства соединений. Так, например в международном банке структурных данных только для органических соединений содержится информация о структурах более 400 000 тысяч. Одна из этих структур, полученная в ВлГУ, приведена на рисунках. 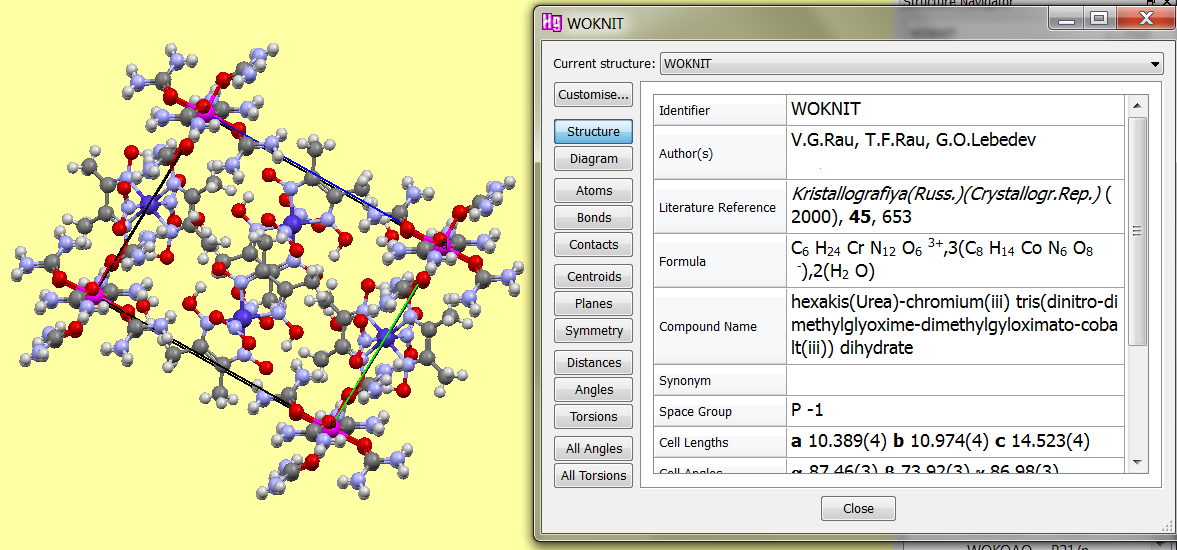 Лекция 15. Спонтанное и индуцированное излучение. Лазеры. План лекции: Рассмотреть природу спонтанного и индуцированного излучения. Устрой- ство и принцип действия лазеров. Применение лазеров. Пусть излучающая системой является атом. Излучение (эмиссия) любого электромагнитного излучения происходит в результате переходов атомов из состояния с большей энергией (возбужденные состояния) в состояние с меньшей энергией (см. рисунок). 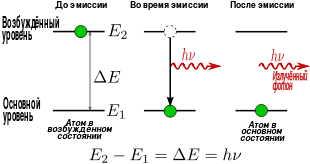 Если атом находится в состоянии с минимальной энергией – это устойчивое невозбужденное состояние. Время жизни атома в этом состоянии стремится к бесконечности. Если атом поглотил энергию равную разности двух состояний 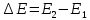 , то он перешел в возбужденное состояние – атом возбудили. , то он перешел в возбужденное состояние – атом возбудили.Время жизни в возбужденном состоянии мало 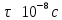 . Атом самопроизвольно переходит из состояния с энергией Е2 в состояние Е1. Этот вид излучения называется спонтанным. При этом атомы излучают не согласованно по фазе. Поэтому спонтанное излучение не когерентно, немонохроматично, не направленно. . Атом самопроизвольно переходит из состояния с энергией Е2 в состояние Е1. Этот вид излучения называется спонтанным. При этом атомы излучают не согласованно по фазе. Поэтому спонтанное излучение не когерентно, немонохроматично, не направленно. Кроме спонтанного излучения было открыто вынужденное или индуцированное излучение атомной системы. Система (газ, твердое тело и т.д.) находится в состоянии статистического равновесия, если все внешние параметры (объем, состав, внешние поля, температура) постоянны. При этом условии среднее число атомов, переходящих из какого-либо стационарного состояния m в состояние n, равно числу обратных переходов. Вследствие этого, среднее число атомов, находящихся в том или ином стационарном состоянии постоянно, т.е. не меняется с течением времени. Обозначим среднее число атомов в состоянии n через Nn, а общее число атомов - через N. Отношение Nn/N определяет долю атомов, которые находятся в возбужденном состоянии n. Эта величина определяет вероятность n-го состояния. Найдем отношение чисел атомов N1 и N2, находящихся в двух возбужденных состояниях 1 и 2. Для этого учтем, что число атомов, находящихся в различных энергетических состояниях, описывается статистической формулой Больцмана: 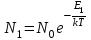 и и 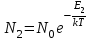 где N0 - число атомов на некотором энергетическом уровне, принятом за начало отсчете энергии. Таким образом, 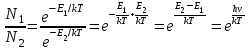 Отсюда следует, что при E1>E2 отношение N1/N2 меньше единицы, т.е. чем больше энергия состояния, тем меньше атомов в таком состоянии. Такое распределение атомов по возбужденным состояниям имеет место при статистическом равновесии. В неравновесной системе оно может быть нарушено. Такое нарушение и имеет место в квантовых генераторах света. Из последней формулы в частности следует, что в равновесном состоянии наибольшее число атомов находится в основном состоянии. Как известно из курса общей физики, излучение нагретых тел подчиняется формуле Планка: 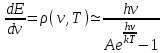 , ,где hv - энергия кванта света, а величина 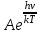 характеризует долю возбужденных состояний с частотой v . характеризует долю возбужденных состояний с частотой v .Квантовая теория позволяет вычислить вероятности различных спонтанных переходов. Их принято обозначать буквой с соответствующими индексами, которые указывают номера уровней. Если при расчете окажется, что вероятность перехода равна нулю, то такой переход не будет осуществляться (запрещенный переход). Таким образом, если система находится в статистическом равновесии, то условие равновесия можно записать следующим образом: 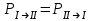 , ,если рассматривать только два возможных состояния I и II . Вероятность 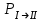 пропорциональна количеству фотонов в среде и числу атомов в невозбужденном состоянии (на уровне I). пропорциональна количеству фотонов в среде и числу атомов в невозбужденном состоянии (на уровне I).Если переход из II-го состояния в первое совершается самопроизвольно, то 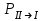 зависит только от количества атомов в возбужденном состоянии. В этом случае условие равновесия запишется так: зависит только от количества атомов в возбужденном состоянии. В этом случае условие равновесия запишется так: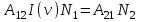 (*) (*)Отсюда 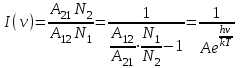 . .Полученное равенство не согласуется с законом излучения, поэтому будем исходить из формулы Планка, которую можно записать: 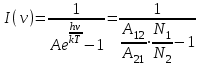 откуда после преобразований имеем: 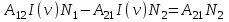 , т.е. , т.е. 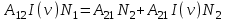 (**) . (**) .Это уравнение баланса впервые было получено Эйнштейном, поэтому вероятности переходов Aij называют коэффициентами Эйнштейна. Сравнивая формулы (*) и (**) можно сделать вывод, что переход I—>II характеризуется не только количеством фотонов в возбужденном состоянии, но и зависит от общего числа фотонов. Таким образом, А.Эйнштейном был сделан вывод, что переход из возбужденного состояния в основное или в более низкое состояние может происходить не только самопроизвольно, но и под действием других фотонов. При этом также происходит излучение, которое называется вынужденным или индуцированным. В отличии от спонтанного, индуцированное излучение когерентно, монохроматично, узко направлено и поляризовано. Источники индуцированного излучения в оптическом диапазоне называются оптическими квантовыми генераторами (ОКГ), так как при прохождении фотонов в среде, с определенными свойствами, излучение усиливается . ОКГ в видимом диапазоне называются лазерами.    Лазеры, благодаря своим свойствам находят широкое применение во всех областях современной науки, техники, технологиях и быту. Лекция 16. Состав и строение атомного ядра. План лекции. Экспериментальные факты, подтверждающие сложное строение атома ядра. Состав и строение атомного ядра. Радиоактивность и туннельный эффект. Ядерные силы. В конце XIX века были получены экспериментальные факты, говорившие о сложном строении ядра, в опыте Резерфорда размер ядра 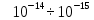 м мОдним из важных опытов в развитии атомной физики сыграло открытие радиоактивности (естественной радиоактивности). В 1896 г. Беккерель обнаружил опытно, что соли урана самопроизвольно испускают излучение, обладающее большой проникающей способностью. Позже Мари Склодовская-Кюри и Пьер Кюри показали, что кроме урана излучает и имеющиеся в нем примеси. Это позволило им открыть два новых элемента: радий (лучистый) и полоний. Было показано, что это излучение состоит из трех компонентов: 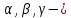 излучения. излучения. Всякое самопроизвольное испускание радиоактивными веществами 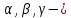 излучения в результате, которых ядра одних элементов превращаются в другие получило название естественной радиоактивность. Эти ряды излучений исследовались в магнитных и электрических полях. Был сделан вывод, что излучения в результате, которых ядра одних элементов превращаются в другие получило название естественной радиоактивность. Эти ряды излучений исследовались в магнитных и электрических полях. Был сделан вывод, что 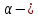 излучение – поток ядер атомов гелия излучение – поток ядер атомов гелия 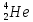 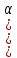 (положительно заряженная частица); (положительно заряженная частица); 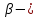 излучение – поток быстрых электронов излучение – поток быстрых электронов 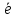 (положительно заряженная частица); (положительно заряженная частица); 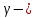 электромагнитное излучение, более коротковолновое, чем рентгеновское. Такие ядерные превращения говорят о сложном строение атомного ядра. электромагнитное излучение, более коротковолновое, чем рентгеновское. Такие ядерные превращения говорят о сложном строение атомного ядра. В конце XIX века получены результаты, которые показали, что продукты радиоактивного распада в большинстве случаев сами радиоактивны. Были обнаружены атомы, ядра которых имеют одинаковый положительный заряд 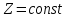 , но разное массовое число , но разное массовое число 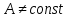 . Такие ядра были названы изотопами. Например, для ядра атома водорода: . Такие ядра были названы изотопами. Например, для ядра атома водорода: 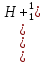 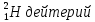 , , 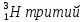 .Изотопы есть и у ядер тяжелых элементов. .Изотопы есть и у ядер тяжелых элементов. 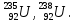 Как известно, естественная система химических элементов заканчивается 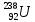 искусственным путем были созданы элементы с атомными номерами Z искусственным путем были созданы элементы с атомными номерами Z 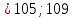 все они оказались неустойчивыми. Все ядра А>210 – неустойчивые. все они оказались неустойчивыми. Все ядра А>210 – неустойчивые. Радиоактивные превращения происходят на законах: закон сохранения заряда, закон сохранения массы. 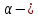 распад: распад: 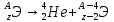 ; ; 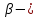 распад: распад: 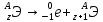 . .Распад ядер носит статистический характер. Невозможно сказать, когда именно распадется данное ядро, но можно определить вероятность распада. Закон радиоактивного распада 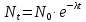 , где , где 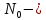 начальное число ядер, а начальное число ядер, а 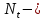 число нераспавшихся ядер в момент времени t, число нераспавшихся ядер в момент времени t, 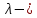 постоянная распада численно равная вероятности распада одного ядра за секунду. постоянная распада численно равная вероятности распада одного ядра за секунду.Теоретически все ядра распадаются за бесконечно большой промежуток времени, поэтому для характеристики скорости распада вводится величина – период полураспада Т. Т – время, за которое распадается половина наличных ядер. 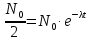 , , 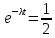 , , 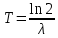 , , 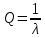 - среднее время жизни атома ядра. - среднее время жизни атома ядра.Изменение числа ядер при радиоактивном распаде можно представить графически. 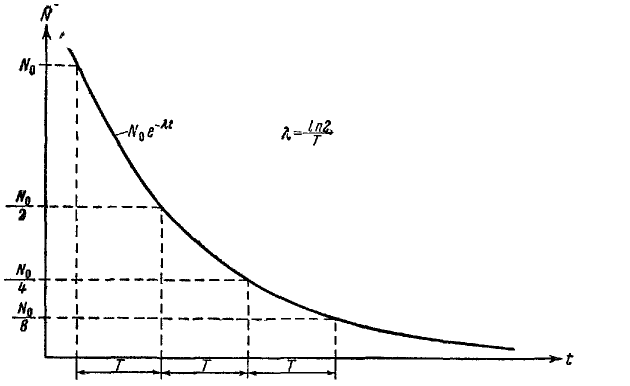 Период полураспада различных элементов резко отличается: от долей секунды до миллиардов лет.  . Открытие естественной радиоактивности, получение изотопов, искусственная радиоактивность говорят о сложном строение атомного ядра. . Открытие естественной радиоактивности, получение изотопов, искусственная радиоактивность говорят о сложном строение атомного ядра. Искусственная радиоактивность позволила открыть протон и нейтрон. В 1919 г. Резерфорд открыл протон: 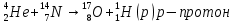 . .В 1932 г Чедвик открыл нейтрон 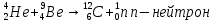 Массы протона и нейтрона сравнимы между собой. Судя по величине Z в состав ядра гелия должно входить два протона и два нейтрона. Таким образом справедлива протонно-нейтронная модель ядра. Обозначим количество протонов Z, число нейтронов - N . Их называют нуклонами. Z+N=A, А – атомная масса. Таким образом, объяснено существование изотопов. Например, 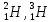 Z=const, N Z=const, N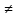 const. const. Рассмотрим природу ядерных сил. По гипотезе Иваненко, Тамма нуклоны в ядре испытывают непрерывное превращение, как бы радиоактивный распад: нейтрон испускает электрон и превращается в протон, а протон поглотив этот электрон превращается в нейтрон. Таким образом, между нуклонами всегда существует легкая частица – электрон, которая и обеспечивает взаимодействия нуклонов. Эта теория приводит к малой величине сил взаимодействия. Японский физик Юкава предположил, что взаимодействие нуклонов осуществляется более тяжелыми частицами. Подобные частицы были открыты в космических лучах в 1937 году – называются µ- мезоны, но оказалось, что мезоны ядерно неактивны, они с нуклонами не взаимодействуют, позже были открыты другие частицы π- пи-мезоны ( 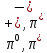 они оказались активными. В настоящее время доказано, что именно пионы являются носителями ядерных сил, т.е. нуклоны в ядре обмениваются пи-мезонами, которые переносят импульс, и обуславливают притяжение нуклонов. Ядерные силы носят обменный характер. они оказались активными. В настоящее время доказано, что именно пионы являются носителями ядерных сил, т.е. нуклоны в ядре обмениваются пи-мезонами, которые переносят импульс, и обуславливают притяжение нуклонов. Ядерные силы носят обменный характер.Ядерные силы –короткодействующие силы, радиус действия 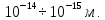 , не являются центральными силами, значительно превосходит кулоновские силы и силы магнитного взаимодействия, т.к. эти силы быстро убывают с расстоянием, радиус действия их мал, они действуют между соседними нуклонами Им присуще свойство насыщения; наиболее устойчивое образование из четырех нуклонов (𝛼-частица). , не являются центральными силами, значительно превосходит кулоновские силы и силы магнитного взаимодействия, т.к. эти силы быстро убывают с расстоянием, радиус действия их мал, они действуют между соседними нуклонами Им присуще свойство насыщения; наиболее устойчивое образование из четырех нуклонов (𝛼-частица). Зная состав ядер, можно дать объяснение естественной радиоактивности на примере α - распада ядер тяжелых элементов. 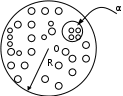 Будем рассматривать ядро тяжелого элемента, состоящего из большого числа нуклонов, способных образовать α -частицу как часть ядра. Все частицы находятся в "тепловом" хаотическом движении внутри ядра (капельная модель Бора-Френкеля). Будем рассматривать ядро тяжелого элемента, состоящего из большого числа нуклонов, способных образовать α -частицу как часть ядра. Все частицы находятся в "тепловом" хаотическом движении внутри ядра (капельная модель Бора-Френкеля).При r < R-частица находится в одинаковых условия с точки зрения окружения ее остальными нуклонами ядра и осуществляет взаимодействие лишь с ближайшими "соседями", т.к. ядерные силы короткодействующие. Поэтому потенциальная энергия взаимодействия α -частицы с ядром постоянна: 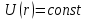 . Энергия взаимодействия отрицательна. При r > R(α -частица вне ядра) ядерные силы практически не влияют на поведение α -частицы. Существенно лишь кулоновское отталкивание: . Энергия взаимодействия отрицательна. При r > R(α -частица вне ядра) ядерные силы практически не влияют на поведение α -частицы. Существенно лишь кулоновское отталкивание: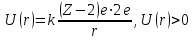  Н Н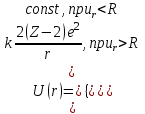 аконец, при r ≈ R, ядерные сила ослаблены и кулоновское отталкивание постепенно становится с ними сравнимым по величине. График U(r) при всех r представлен на рисунке. Если в качестве ядра выбрать RаС , то полная энергия вылетевшей α -частицы вдали от ядра (при r >>R) совпадает с кинетической, которая по измерениям равна≈ 7 МэВ. Способна ли α -частица вырваться из ядра, если потенциальная энергия удерживающих сил не меньше 30 МэВ? Если α -частица классическая, то для нее вылет из ядра запрещен, но для микрообъекта важно оценить вероятность ее появления вне "барьера". Если волновые свойства α-частицы таковы, что неопределенность в ее координате больше ширины барьера, то она может оказаться вне ядра. Запишем соотношение Гейзенберга: аконец, при r ≈ R, ядерные сила ослаблены и кулоновское отталкивание постепенно становится с ними сравнимым по величине. График U(r) при всех r представлен на рисунке. Если в качестве ядра выбрать RаС , то полная энергия вылетевшей α -частицы вдали от ядра (при r >>R) совпадает с кинетической, которая по измерениям равна≈ 7 МэВ. Способна ли α -частица вырваться из ядра, если потенциальная энергия удерживающих сил не меньше 30 МэВ? Если α -частица классическая, то для нее вылет из ядра запрещен, но для микрообъекта важно оценить вероятность ее появления вне "барьера". Если волновые свойства α-частицы таковы, что неопределенность в ее координате больше ширины барьера, то она может оказаться вне ядра. Запишем соотношение Гейзенберга: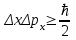 . Если нас интересует . Если нас интересует 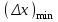 , то от неравенства можно перейти к равенству , то от неравенства можно перейти к равенству 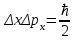 . .Откуда 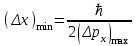 . Наибольшая неопределенность в импульсе соизмерима с самим импульсом, а тогда . Наибольшая неопределенность в импульсе соизмерима с самим импульсом, а тогда 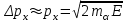 ; ;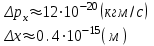 Толщина "барьера" d не превышает размеров ядра 10-15 м и уже отсюда видно, что d и 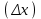 соизмеримы, поэтому у α -частицы есть вероятность оказаться вне ядра. соизмеримы, поэтому у α -частицы есть вероятность оказаться вне ядра.Решим задачу по теме. Определить, сколько ядер в m0 - 1.0 мг радиоизотопа церия 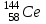 распадается в течение промежутков времени: 1) Δt= 1 c; 2) Δt = 1 год. распадается в течение промежутков времени: 1) Δt= 1 c; 2) Δt = 1 год. Период полураспада церия Т = 285 суток. Решение. (1) Так как Δt << Т, то можно считать, что за Δt число нераспавшихся ядер остается практически постоянным и равным их начальному числу N0. Тогда число распавшихся ядер за время Δt определяется по закону: 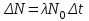 или или 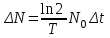 .Начальное число ядер (атомов) N определим, умножив число Авогадро NA на число молей ν, содержащихся в данном препарате, .Начальное число ядер (атомов) N определим, умножив число Авогадро NA на число молей ν, содержащихся в данном препарате,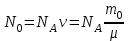 , где μ-молярная масса изотопа , где μ-молярная масса изотопа 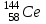 , численно равная (приблизительно) его массовому числу: , численно равная (приблизительно) его массовому числу: 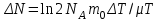 В СИ: 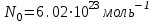 ; ; 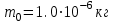 ; Δt = 1c ; Δt = 1c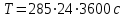 ; ; 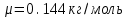 ; ; 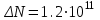 ; ;(2).Δt и Т -величины одного порядка. Число ядер, распадающихся за Δt равно: 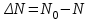 , где , где 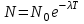 , , 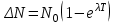 или или 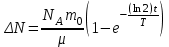 , т.к. , т.к. 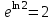 , то , то 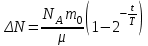 , , 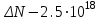 Лекция 17. Энергия связи ядра. Ядерные реакции. Цепные реакции деления и синтеза. Ядерная энергетика. План лекции. Рассмотреть энергию связи ядра, реакции деления ядер тяжелых элементов, реакции синтеза легких элементов. Управляемый термоядерный синтез, ИТЭР. Атомное ядро – стабильное образование. Стабильность ядра характеризуется энергией связи ядра. Энергия связи равна энергии необходимой для разделения ядра на составные части. При делении ядра должны выполняться законы: закон сохранения заряда и закон сохранения энергии. По формуле Эйнштейна, известной из его теории относительности 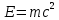 . Пусть ядро делится на две составные части . Пусть ядро делится на две составные части 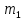 и и 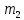 Запишем закон сохранения энергии: Запишем закон сохранения энергии: 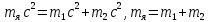 Расчет показывает, что для 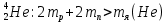 . Величина, равная разности масс частиц , составляющие ядро и массой ядра называют дефектом масс. . Величина, равная разности масс частиц , составляющие ядро и массой ядра называют дефектом масс. 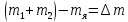 - дефект масс. Закон сохранения энергии запишется: - дефект масс. Закон сохранения энергии запишется: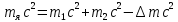 , который читается: энергия системы (ядро) складывается из кинетической энергии составных частей и потенциальной энергии их взаимодействия, т.е. энергия связывающая их в единую систему (потенциальная энергия всегда отрицательна). Модуль , который читается: энергия системы (ядро) складывается из кинетической энергии составных частей и потенциальной энергии их взаимодействия, т.е. энергия связывающая их в единую систему (потенциальная энергия всегда отрицательна). Модуль 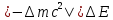 – энергия связи. – энергия связи. При образовании ядра эта энергия выделяется, а при распаде – поглощается извне (см. рисунок). Выражая энергию связи через характеристики ядра, получим: Δm = MЯ– (Zmp + Nmn). 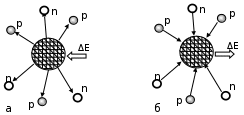 Для характеристики прочности атомного ядра вводят понятие энергии связи и дефекта масс приходящиеся на один нуклон – это есть удельная энергия связи. Зависимость энергии связи от атомной массы изотопов представлена на рисунке. 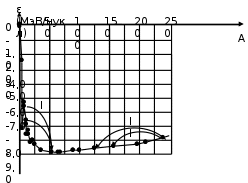 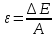 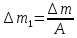 Ядро тем прочнее, чем больше удельная энергия связи и дефект масс, т.е. чем меньше потенциальная энергия системы. Самые прочные ядра расположены в средней части таблицы Менделеева с атомной массой А Ядро тем прочнее, чем больше удельная энергия связи и дефект масс, т.е. чем меньше потенциальная энергия системы. Самые прочные ядра расположены в средней части таблицы Менделеева с атомной массой А . Такая зависимость удельной энергии связи от А дает энергетически выгодным два процесса: . Такая зависимость удельной энергии связи от А дает энергетически выгодным два процесса:деление тяжелых ядер на несколько более легких: 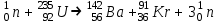 ; ;слияние (синтез) легких ядер в одно ядро 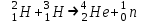 . .Если характеризовать энергетическое состояние ядра величиной 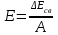 (энергией связи на один нуклон), то процесс "рождения" и распада ядра можно представить двухуровневой системой (диаграмма): (энергией связи на один нуклон), то процесс "рождения" и распада ядра можно представить двухуровневой системой (диаграмма):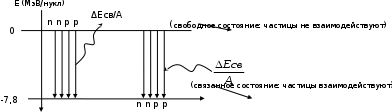 Аналогично, через дефект масс можно вычислить величину Е для всех ядер периодической системы элементов: 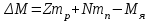 . Построенный по значениям Е (МэВ/нукл) график для ядер периодической системы элементов, показывает, что наиболее устойчивы нуклоны в ядрах, принадлежащих средней части таблицы Менделеева и потому перевод их в эти состояния должен быть энергетически выгодным: для ядер тяжелых элементов выгоден распад, а для легких элементов - синтез. Эти процессы изображены на диаграммах: . Построенный по значениям Е (МэВ/нукл) график для ядер периодической системы элементов, показывает, что наиболее устойчивы нуклоны в ядрах, принадлежащих средней части таблицы Менделеева и потому перевод их в эти состояния должен быть энергетически выгодным: для ядер тяжелых элементов выгоден распад, а для легких элементов - синтез. Эти процессы изображены на диаграммах:а) реакция распада 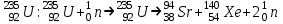 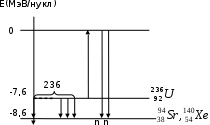 Расчет реакции: 236(-8,6+7,6)+2(0 + 8,6)= -236,0 +17,2 = -218,8 (МэВ). 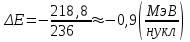 . В результате реакции выделяется 0,9 МэВ на один нуклон. . В результате реакции выделяется 0,9 МэВ на один нуклон. б) реакция синтеза: 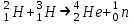 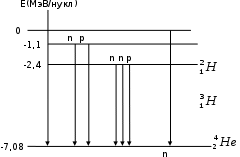 Расчет реакции: 2(-7,08+1,1)+3(-7,08+2,4)+ +1(0,+7,08)=-11,96-14,04+ +7,08=-18,9(МэВ) 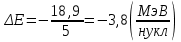 . .В результате реакции выделяется 3,8 МэВ на один нуклон. Выгодность реакции синтеза легких элементов перед реакцией распада тяжелых ядер очевидна. Технически реакция распада легче осуществима, так как она происходит без внешних затрат, а реакция синтеза требует слияния ядер легких элементов, на что расходуется энергия по преодолению кулоновского отталкивания. Цепные реакции деления ядер тяжелых трансурановых элементов и реакции синтеза легких элементов (изотопов водорода) сопровождаются выделением большого количества энергии. На практике эти процессы используются для получения атомной ядерной энергии. Первый тип реакций – деления ядер называется цепной реакцией, которая идет в реакторе (рисунок).  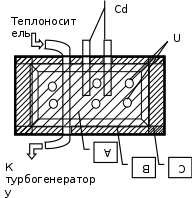 Проблема получения управляемой термоядерной реакции синтеза легких элементов (УТС) решается усилиями многих стран в проекте ИТЭР . ИТЭР (ITER) - это международный проект, цель которого продемонстрировать научную и техническую осуществимость получения энергии за счет термоядерной реакции. Партнерами проекта являются Евросоюз (the European Union) (представленный Евроатомом (EURATOM) ), Япония (Japan), Китай (the People's Republic of China), Индия (India), Южная Корея (the Republic of Korea), Российская Федерация (the Russian Federation) и США (USA). ИТЭР будет построен в Европе, во французском местечке Кадараше (Cadarache). В случае успешной реализации проекта появится возможность получения неисчерпаемого источника экологически чистой энергии. Стоит отметить, что основой ИТЭР стало использование тороидальной камеры с магнитными катушками (рисунок), создание которой предложили еще советские ученые-термоядерщики в 1985 году.  Сегодня это название уже официально не является аббревиатурой, а связано с латинским словом ITER (в пер. путь). Решим задачи. 1. Определить удельную энергию связи для ядра 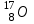 . .Решение. Удельная энергия связи ядра, равна отношению его энергии связи ΔW к массовому числу (числу нуклонов в ядре) А: 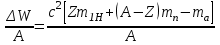 ; ; 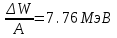 2. Счетная трубка, предназначенная для счета медленных нейтронов, покрывается с внутренний стороны соединением, содержащим изотоп 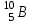 . Определить энергию, которая выделяется при реакции, происходящей в результате удара нейрона о внутреннюю поверхность трубки. . Определить энергию, которая выделяется при реакции, происходящей в результате удара нейрона о внутреннюю поверхность трубки.Решение. Известно, что при захвате нейтрона 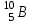 превращается в изотоп превращается в изотоп 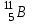 , который распадается на , который распадается на 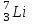 и α -частицу, которая обнаруживается по ее ионизирую- и α -частицу, которая обнаруживается по ее ионизирую-щему действию и регистрируется счетным устройством. Происходящая при этом ядерная реакция имеет вид: 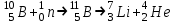 . . Для вычисления энергии, выделяемой при данной реакции, определим дефект массы реакции: 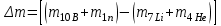 ,энергия, выделяемая в реакции: ,энергия, выделяемая в реакции: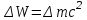 3. Атомная электростанция мощностью 500000 кВт имеет к.п.д. 20 %. а) Определить годовой расход ядерного горючего, если за каждый акт деления 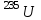 выделяется 200 МэВ энергии; выделяется 200 МэВ энергии; б) сравнить полученный результат с годовым расходом каменного угля тепловой электростанции той же мощности при к.п.д. 75%. Решение а) Годовой расход ядерного горючего можно определить по числу ядер 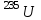 , распавшихся за год: n = Q/g, где Q –тепловой эффект годовой работы, Q - тепловой эффект одного акта деления. Величину Q можно выразить: , распавшихся за год: n = Q/g, где Q –тепловой эффект годовой работы, Q - тепловой эффект одного акта деления. Величину Q можно выразить: 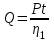 Q , тогда Q , тогда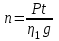 . Массу ядерного горючего m1 израсходованного атомной электростанцией за год можно определить: . Массу ядерного горючего m1 израсходованного атомной электростанцией за год можно определить: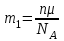 , ,где μ - молярная масса изотопа, численно равная его массовому числу (приблизительно), NA - число Авогадро. Тогда 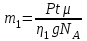 ; m1 = 965 кг. ; m1 = 965 кг.б) Тепловая электростанция той же мощности, за то же время потребляет каменного угля: 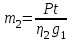 ,где g1 - теплотворная способность топлива ,где g1 - теплотворная способность топлива (g1 = 7000 ккал/кг = 2,93∙107 Дж/кг). Получим m2 =7.16∙108кг Т.е. ядерного горючего по массе требуется почти в миллион раз меньше, чем каменного угля. |
