Курс лекций. Курс лекций ОЭФ(Кв) 14 (копия). Курс лекций по дисциплине Общая и экспериментальная физика для студентов ВлГУ
 Скачать 7.12 Mb. Скачать 7.12 Mb.
|
|
Лекция 7. Рентгеновское излучение. План лекции. Рассмотреть историю открытия рентгеновского излучения, его свойства; получение тормозного рентгеновского излучения. Одним из важнейших открытий конца ХIХ века явилось обнаружение в 1895 г. немецким физиком Рентгеном лучей, названных впоследствии его именем и представляющих собой короткие электромагнитные волны. Эти лучи имеют ряд замечательных свойств: 1) В отличие от световых лучей рентгеновские лучи не воспринимаются непосредственно глазом наблюдателя. Однако они вызывают свечение некоторых веществ (например, платино-синеродистого бария), действуют на эмульсию фотопластинок и вызывают ионизацию газов. Для обнаружения и изучения свойств рентгеновских лучей могут быть, следовательно, использованы три метода: визуальный (метод флюоресцирующих экранов), фотографический и ионизационный. Первый является наиболее грубым, последний – наиболее чувствительным. 2) Рентгеновские лучи проходят сквозь тела, не прозрачные для видимого света. Ослабление интенсивности рентгеновских лучей зависит от плотности и природы вещества, лежащего на их пути. Чем больше плотность вещества и больше атомные номера элементов, входящих в его состав, тем значительнее поглощение лучей. Благодаря своей высокой проникающей способности рентгеновские лучи сразу нашли широкое применение в технике и медицине. 3) Рентгеновские лучи оказывают значительное физиологическое воздействие на живые организмы. Они применяются в медицине не только как диагностическое средство, но и в качестве терапевтического – как при лечении кожных заболеваний, так и при лечении заболеваний внутренних органов. Однако в больших дозах рентгеновские лучи чрезвычайно вредны. Они вызывают болезненные ожоги и могут нанести непоправимый вред всему организму в целом. 4) Рентгеновские лучи распространяются прямолинейно, в электрическом и магнитном полях не отклоняются. При прохождении через вещество они очень незначительно преломляются и могут испытывать полное внутреннее отражение от гладкой поверхности, если угол между падающим лучом и поверхностью меньше 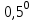 . .1912 году немецкий физик М.Лауэ получает дифракцию нового вида излучения: х-лучи на кристалле. Рентгеновское излучение – это электромагнитное излучение, коротковолновое излучение 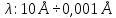 (ангстрем (ангстрем 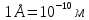 ). ).Рентгеновские лучи возникают при торможении веществом быстрых электронов. В лабораториях эти лучи получаются в рентгеновской трубке (рисунки), состоящей из вакуумированного стеклянного или металлического корпуса, в котором на определенном расстоянии друг от друга находятся катод и анод, включенные в цепь высокого напряжения. Катод служит источником электронов, а анод (антикатод) – источником рентгеновских лучей. 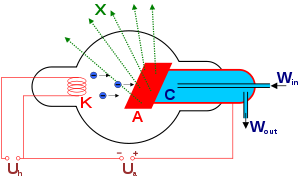   В процессе ускорения-торможения лишь около 1% кинетической энергии электрона идёт на рентгеновское излучение, 99% энергии превращается в тепло. Чтобы предотвратить перегрев анода, в мощных рентгеновских трубках применяют водяное охлаждение и вращающийся анод. Энергия генерируемых фотонов лежит в области рентгеновского диапазона (длина волны 0,05 ÷ 0,2 нм). Если энергия электронов не превышает некоторого значения, характерного для вещества анода, то возникает сплошной спектр рентгеновского излучения всевозможных длин волн (тормозное излучение или белое). В противном случае возникает характеристическое излучение (т.е. характеризующее вещество тормозящей поверхности), спектр которого линейчатый (рисунок). 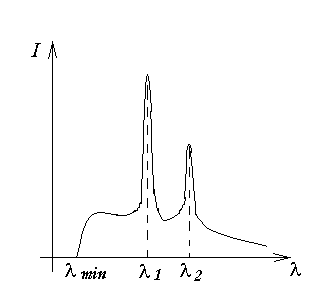 Спектр рентгеновского излучения Закономерности, которым подчиняются длины волн и интенсивности 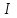 этих спектров, различны. Особенности сплошного спектра определяются в большей мере режимом работы трубки (приложенным напряжением и силой тока), чем веществом анода; наоборот, длины волн линейчатого спектра зависят исключительно от вещества анода. этих спектров, различны. Особенности сплошного спектра определяются в большей мере режимом работы трубки (приложенным напряжением и силой тока), чем веществом анода; наоборот, длины волн линейчатого спектра зависят исключительно от вещества анода.На рисунках, а,b,в показаны кривые распределения интенсивности сплошного спектра по длинам волн при различных напряжениях на трубке (рис.а), различной силе тока (рис.b) и различном материале анода (рис.в). Эти кривые показывают, что интенсивность излучения с данной длиной волны тем больше, чем выше напряжение 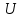 , чем больше сила тока , чем больше сила тока 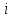 и чем больше атомный номер вещества и чем больше атомный номер вещества 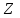 . Общая энергия сплошного спектра определяется приближенно следующим соотношением: . Общая энергия сплошного спектра определяется приближенно следующим соотношением: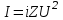 . . 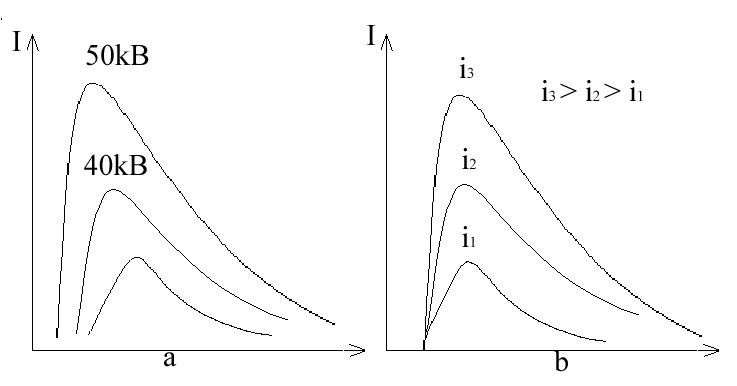 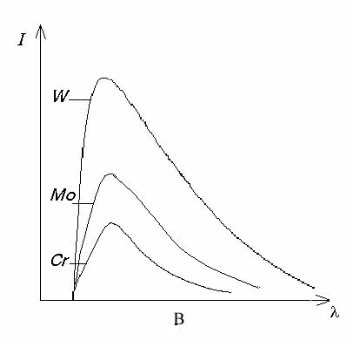 С точки зрения классической электродинамики, возникновение сплошного спектра объясняется резким торможением электронов в поле ядер атомов, из которых состоит анод. Торможение каждого электрона в тонком поверхностном слое анода создает электромагнитный импульс, который можно рассматривать как сумму бесконечного числа налагающихся друг на друга электромагнитных волн различных длин от нуля до бесконечности (теорема Фурье). Так как анод непрерывно бомбардируется электронами, то совокупность электромагнитных импульсов воспринимается как непрерывный поток лучей, имеющих различные длины волн. Однако классическая теория не может объяснить обрыв сплошного спектра со стороны коротких длин волн. С точки же зрения квантовой теории наличие коротковолновой границы 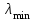 вполне понятно. Кинетическая энергия каждого электрона при торможении анодом может перейти (частично или полностью) либо во внутреннюю энергию вещества анода (анод нагревается), либо в энергию одного или нескольких квантов рентгеновского излучения. В зависимости от того, какая часть кинетической энергии электрона переходит в энергию кванта вполне понятно. Кинетическая энергия каждого электрона при торможении анодом может перейти (частично или полностью) либо во внутреннюю энергию вещества анода (анод нагревается), либо в энергию одного или нескольких квантов рентгеновского излучения. В зависимости от того, какая часть кинетической энергии электрона переходит в энергию кванта 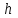 , частота излучений будет различной. В тех случаях, когда вся кинетическая энергия электрона превращается в один квант излучения, частота излучения будет максимальна, а длина волны минимальна. , частота излучений будет различной. В тех случаях, когда вся кинетическая энергия электрона превращается в один квант излучения, частота излучения будет максимальна, а длина волны минимальна.Кинетическая энергия электрона равна работе, совершенной силами электрического поля по переносу его от катода к аноду, т.е. 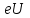 , где , где 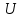 – напряжение, – напряжение, 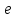 – заряд электрона. – заряд электрона.Энергия кванта равна 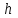 = = 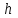 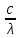 , где с – скорость света. Торможение электронов на аноде подчиняется закону сохранения и превращения энергии: , где с – скорость света. Торможение электронов на аноде подчиняется закону сохранения и превращения энергии: eU = hν + Eтепловая ; hνmax= eU. Следовательно, минимальная длина волны определяется напряжением на трубке соотношением: 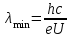 . Длина волны коротковолновой границы спектра тем меньше, чем выше напряжение на трубке. Если длины волн измерять в нанометрах, а напряжение – в киловольтах, то . Длина волны коротковолновой границы спектра тем меньше, чем выше напряжение на трубке. Если длины волн измерять в нанометрах, а напряжение – в киловольтах, то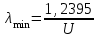 . . Рассчитаем минимальную длину волны рентгеновского тормозного излучения в задаче: Определить минимальную длину волны в сплошном спектре рентгеновского излучения, если рентгеновская трубка работает при напряжении U = 30 кВ. Решение. Сплошной рентгеновский спектр возникает вследствии торможения электронов, разогнанных в трубке электрическим полем, при их ударах об антикатод. Существование коротковолновой границы сплошного рентгеновского спектра вытекает из квантовой природы излучения. Действительно, подлетая к антикатоду, электрон облагает кинетической энергией Ек, равной работе, совершенной над ним силами электрического поля, т.е Ек.=eU . При ударе об антикатод энергия электрона ек частично или полностью превращается в квант энергии hν . Наибольшей частоте (наименьшей длине волны) соответствует случай, когда вся энергия Ек превращается в квант hν . Тогда 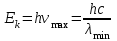 ; ; 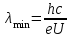 .Подставим числовые значения в СИ: .Подставим числовые значения в СИ:h = 6.62∙10-34 Дж∙с;с = 3,00∙108 м/с;е = 1,6∙10-19 Кл;U = 3,0∙104 В.Получим λmin = 0.41∙10-10 м = 0,41Å. Лекция 8. Эффект Комптона. План лекции: Рассмотреть открытие эффекта Комптоном. Дать анализ физических процессов и произвести расчет. Блестящим доказательством квантовых свойств излучения является явление, которое изучает в 1923 году американский физик Комптон. Суть этого явления в том, что Комптон рассматривает взаимодействие фотонов больших энергий (рентгеновских диапазонов) со слабо связанными электронами вещества, практически свободными, то есть с электронами для легких веществ (графин, парафин). В явлении фотоэффекта тоже рассматривается взаимодействие фотонов с электронами вещества, но в данном явлении взаимодействуют фотоны оптического диапазона и взаимодействуют со связанными электронами вещества. При этом один фотон полностью передает электрону вещества, при этом электрон покидает металл. В явлении, который изучает Комптон, взаимодействует фотон с электроном вещества, причем: 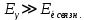 Результатом взаимодействия в рассеянном излучении наряду с длиной волны 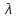 первоначального излучения присутствует длина волны первоначального излучения присутствует длина волны 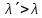 в этом и заключается суть явления Комптона. Оказалось, что в этом и заключается суть явления Комптона. Оказалось, что 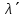 не зависит не от первоначальной длины волны не зависит не от первоначальной длины волны 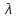 , не от рода вещества, а зависит от угла рассеивания , не от рода вещества, а зависит от угла рассеивания 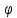 . .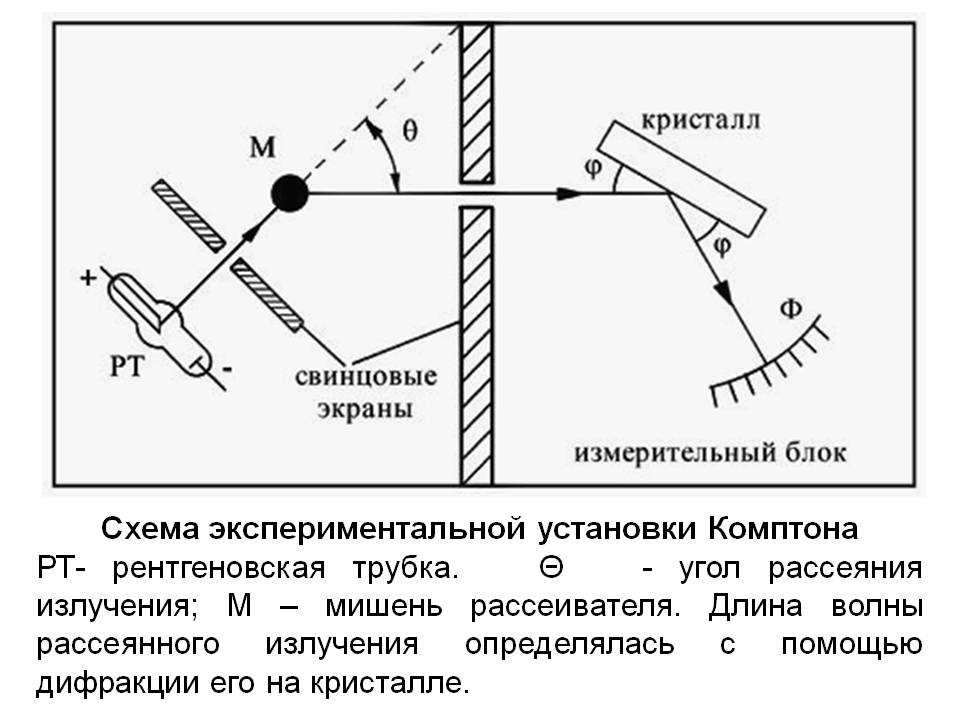 Эффект Комптона – это упругое рассеивание коротковолнового электромагнитного излучения (рентгеновского и гамма-излучения) на свободных (слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. 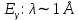 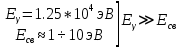 С точки зрения волновой физики электрон поглотил энергию фотона, колеблющийся электрон излучает: частота должна быть равна частоте собственных колебаний, то есть такой электрон будет излучать ту же частоту, которую и поглотил. С точки зрения квантовой физики электрон вещества поглощает энергию падающего фотона и мгновенно излучает энергию 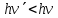 . Сам электрон приобретает энергию равную разности энергии фотонов. . Сам электрон приобретает энергию равную разности энергии фотонов.Электрон при этом приобретает скорость 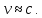 При элементарном процессе рассеивания должны выполняться законы: 1.Закон сохранения и превращения энергии. 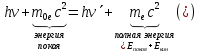 2.Закон сохранения импульса. 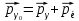 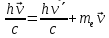 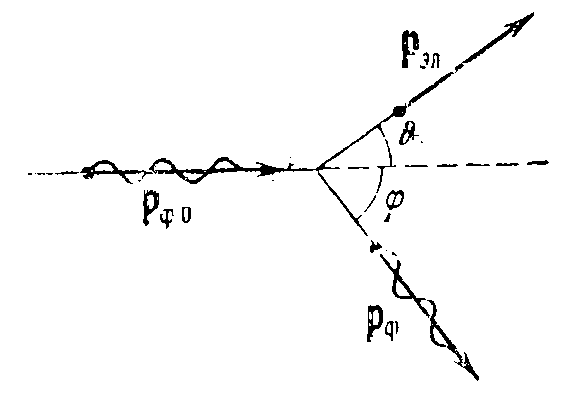 Проекция начального импульса фотона:  Проекция перпендикулярная начальному направлению: 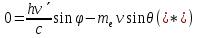 Совместное решение трех уравнений (*),(**),(***) позволяет вывести формулу изменения длины волны при рассеянии фотона: 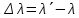 , ,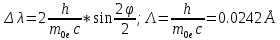 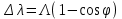 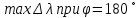 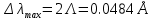 Эффект Комптона показал, что законы изменения импульса и превращении энергии при взаимодействии элементарных частиц выполняется на микроуровне. После публикации Комптоном в начале 1923 года полученных результатов среди физиков осталось мало сомневающихся в реальности фотонов. Сегодня эффект Комптона находит применение в астрофизике: гамма-лучи от космических объектов подвергаются многократному рассеянию, пока их энергия не падает до длин волн рентгеновской части спектра, после чего их можно анализировать на стандартных рентгенографических установках. Подобный детектор был в 1991 году выведен НАСА на орбиту в составе Гамма-лучевой обсерватории имени Комптона. Рассмотрим процессы, происходящие при эффекте Комптона на задаче. Какая энергия рентгеновского фотона с длиной волны λ = 0.003 нм передаётся электрону отдачи при эффекте Комптона? Рассеяние происходит под углом 60°. Решение В явлении Комптона при упругом ударе фотона с электроном, фотон в соответствии с законами сохранения передает свободному электрону часть импульса и энергии. Уменьшение энергии фотона означает уменьшение частоты рентгеновского излучения и увеличение его длины: 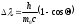 где Θ – угол рассеяния. Из закона сохранения энергии следует: 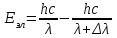 .После вычислений имеем: Еэл = 120 кэВ. .После вычислений имеем: Еэл = 120 кэВ.Лекция 9. Элементы квантовой механики. План лекции: Волны де Бройля. Соотношение неопределенностей Гейзенберга. Волновая функция. Материя как объективная реальность существует в двух видах: поле (фотон), вещество (микрообъект - электрон) материя едина и неделима. В 1924г. Луи де Бройль исходя из единства материального мира, выдвинул смелое предположение о том, что если фотону присущи и корпускулярные, и волновые свойства, следовательно, и микрообъектам вещества- электронам должны быть присущи не только свойства частицы, но и волновые, то есть высказывает гипотезу о волновых свойствах электрона. По аналогии с длиной волны для фотона де Бройль записывает формулу для вычисления длины волны электрона: λБ = h/mv. Волны де Бройля называют волнами материи. В 1929 г. он был удостоен Нобелевской премии за открытие волновых свойств электрона. Говоря о природе волн де Бройля, отметим, что им нет аналогов в классической физике. В макромире волны де Бройля не имеют места. Для примера вычислим длину волны де Бройлы для макро- и микрообъекта: 1. При движении Земли по орбите получим: λБ= 3,6·10-61м.; 2. при движении тела массой 100 г. 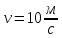 : λБ=6,6·10-33м; : λБ=6,6·10-33м;3. электрон ускорен электрическим полем ( U=1 В): λБ=1нм=10Å. Очевидно, что в первых двух примерах, длина волны слишком мала и не имеетфизического смысла. В последнем случае длина волны электрона соизмерима с длиной волны рентгеновского излучения, то есть имеет физический смысл. В 1927 г. эта гипотеза была впервые подтверждена опытами Дэвиссона и Джермера по дифракции электронов на кристалле никеля, схема которого представлена на рисунке. 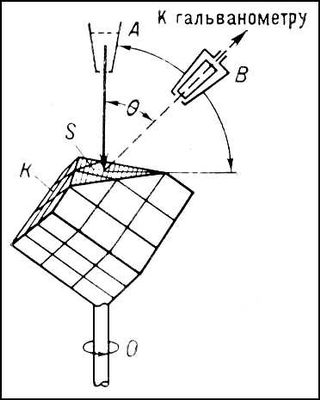 Установка включала в себя монокристалл никеля, сошлифованный под углом и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением на электронной пушке: 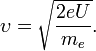 Под углом к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме. В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния Таким образом, , электрон - сложное материальное образование, обладающее, во-первых, волновыми свойствами проявляющимися при дифракции, а во-вторых, электрон обладает корпускулярными свойствами (электрон действует как единое целое). Нильс Бор сформулировал принцип дополнительности: ни волны ни частицы никогда не проявляют одновременно в одном эксперименте и волновые и корпускулярные свойства. Для полного описания явления необходимо использовать и волновые и корпускулярные модели, но каждая из них имеет свою границу приложения. Соотношение неопределенностей Гейзенберга Рассмотрим демонстрацию по дифракции микрообъектов: электронов (либо фотонов) на щели (см.рисунок). 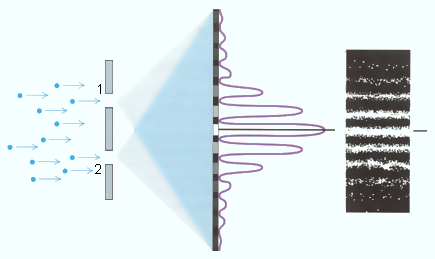 При прохождении микрообъектов через щель шириной Δх непредсказуемо изменяется импульс. Ширина щели определяет точность измерения положения микрообъекта в пространстве и называется неопределенностью в значении координат; неопределенность в значении скорости и импульса обозначим Δрх. Опыт показывает, что Δх и Δрх связаны между собой.: если 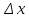 уменьшается, то уменьшается, то 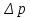 увеличивается; если увеличивается; если 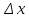 увеличивается, то увеличивается, то 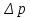 уменьшается и наоборот, но при этом их произведение остается неизменным. Гейзенберг получил соотношение уменьшается и наоборот, но при этом их произведение остается неизменным. Гейзенберг получил соотношение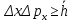 , которое называется соотношением неопределенностей Гейзенберга. Оно читается следующим образом: произведение неопределенности , которое называется соотношением неопределенностей Гейзенберга. Оно читается следующим образом: произведение неопределенности 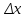 в координате микрообъекта, измеренной в некоторый момент времени на определенность в координате микрообъекта, измеренной в некоторый момент времени на определенность 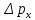 в значении проекции импульса, измеренной в тот же момент времени в значении проекции импульса, измеренной в тот же момент времени 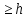 . .Физический смысл: никогда в одном эксперименте одновременно нельзя абсолютно точно измерить и координату микрообъекта, и его импульс. Рассматривая волновые свойства микрообъектов, физики пришли к понятию неопределенности: проводя nизмерений, получаем набор значений величины, то есть каждому значению измеряемой величины соответствует своя вероятность ее появления. Таким образом: волновые свойства микрообъектов – это вероятностные свойства. Каждый волновой процесс характеризуется волновой функцией. Для волн де Бройля такой функцией является 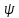 -функция: -функция: 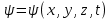 - трехмерный случай. - трехмерный случай. 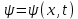 -одномерный случай. Для одномерного случая запишем волновую функцию. -одномерный случай. Для одномерного случая запишем волновую функцию.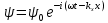 , где , где 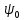 - амплитуда, ω- циклическая частота - амплитуда, ω- циклическая частота 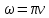 , k- волновой вектор , k- волновой вектор 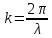 . . Сама 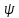 -функци не может быть измерена, так как она является комплексной величиной. Поэтому физический смысл имеет не сама -функци не может быть измерена, так как она является комплексной величиной. Поэтому физический смысл имеет не сама 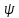 -функция, а квадрат ее модуля : | -функция, а квадрат ее модуля : |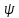 |2 |2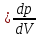 , где , где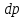 – вероятность обнаружения микрообъекта в соответствующем месте пространства, а – вероятность обнаружения микрообъекта в соответствующем месте пространства, а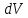 - объем пространства. Тогда - объем пространства. Тогда 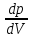 – имеет смысл плотности вероятности. – имеет смысл плотности вероятности.То есть | 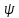 |2-это плотность вероятности обнаружения микрообъектов в соответствующем месте заданного пространства в определенный момент времени. |2-это плотность вероятности обнаружения микрообъектов в соответствующем месте заданного пространства в определенный момент времени.Возвращаясь к природе волн де Бройля отметим: в классической физике нет аналогов волн де Бройля. По предложению Гейзенберга и Борна: волны де Бройля определяют вероятность появления микрообъекта в определенном месте пространства в определенный момент времени. Условно говоря, можно считать, что волны де Бройля - это волны вероятности. Рассчитаем длину волны деБройля для разных случаев: Задача1. Найти длину волны де Бройля для электрона, обладающего энергией: 1) Е =100 эВ;2) Е = 3,0 МэВ Решение. Длина волны де Бройля, соответствующая частице с импульсом р , равна 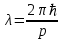 . Необходимо выразить импульс электрона через его кинетическую энергию Е. Решение задачи зависит от того, классической или релятивистской частицей следует считать электрон. . Необходимо выразить импульс электрона через его кинетическую энергию Е. Решение задачи зависит от того, классической или релятивистской частицей следует считать электрон.1) Так как 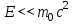 ,где ,где 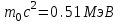 - энергия покоя электрона, то в данном случае электрон является классической частицей. Значит, его импульс и кинетическая энергия связаны соотношением - энергия покоя электрона, то в данном случае электрон является классической частицей. Значит, его импульс и кинетическая энергия связаны соотношением 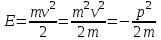 . .Отсюда 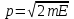 ; длина волны ; длина волны 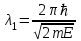 ; ; 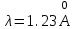 Теперь 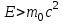 , электрон следует считать релятивистской частицей. Для такой частицы импульс выразится: , электрон следует считать релятивистской частицей. Для такой частицы импульс выразится: 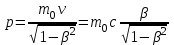 . .Кинетическая (энергия релятивистской частицы вычисляется как разность между полной энергией частицы mc2 и энергией её покоя mc2: 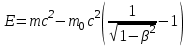 . .Исключив из этих формул β, получим 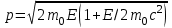 Тогда 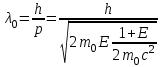 ; ; 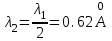 . .Задача 2. Средняя кинетическая энергия электрона в невозбужденном атоме водорода равна 13.6 эВ. Исходя из соотношения Гейзенберга, найти наименьшую неопределенность, с которой можно вычислить координату электрона в атоме. Решение. Соотношение неопределенностей Гейзенберга: 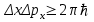 . .Неопределенность координаты частицы 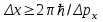 Величина Δрх неизвестна, но так как известна кинетическая энергия частицы, то, зная связь импульса с кинетической энергией, можно определять среднее квадратичное значение импульса. При условии 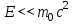 , электрон можно рассматривать как нерелятивистскую частицу, откуда имеем: , электрон можно рассматривать как нерелятивистскую частицу, откуда имеем: 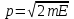 . Наибольшая неопределенность в значении любой величины не превышает самой величины, т.е. . Наибольшая неопределенность в значении любой величины не превышает самой величины, т.е. 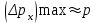 . Поэтому, заменив Δрх величиной р, запишем . Поэтому, заменив Δрх величиной р, запишем 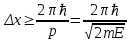 . Вычислив, получим . Вычислив, получим 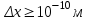 Следовательно, наименьшая, допустимая соотношением неопределенностей неточность 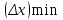 с которой можно определить координату электрона в атоме водорода, есть величина порядка 10-10 м. с которой можно определить координату электрона в атоме водорода, есть величина порядка 10-10 м. Замечание. Предлагается вычислять для атома водорода радиус первой боровской орбиты электрона и сравнить его с величиной неопределенности в значении координаты. Оказывается, что 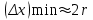 . .Какой вывод можно сделать? Что в данном случае определяется величиной 2r? Задача 3. Параллельный пучок электронов падает нормально на диафрагму с узкой прямоугольной щелью, ширина которой, а = 2,0 мкм. Определить скорость электронов (считая ее одинаковой для всех частиц), если известно, что на экране, отстоящем от щели на расстоянииl = 50 см, ширина центрального дифракционного максимума b = 80 мкм. Решение. Дифракция электронов является следствием волновой природы частиц. Скорость электронов определится 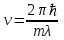 . . Чтобы найти длину волны де Бройля λ , воспользуемся тем обстоятельством,что дифракционная картина, возникающая при прохождении через узкую щель параллельного пучка электронов, вполне соответствует дифракционной картине, полученном от этой же щели при освещении её параллельным пучком монохроматического света, длина волны которого равна длине волны де Бройля для электрона. При дифракции электронов положение дифракционных минимумов можно определить из соотношения: 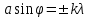 (k = 1,2,3….). При малых углах φ: (k = 1,2,3….). При малых углах φ: 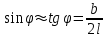 : Полагая k = 1, имеем : Полагая k = 1, имеем 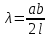 откуда следует, что откуда следует, что 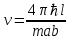 Подставляя данные, получим v = 4.5∙106 м/с Заметим, что v<<c, т.е. электроны нерелятивистские. |
