Курс лекций. Курс лекций ОЭФ(Кв) 14 (копия). Курс лекций по дисциплине Общая и экспериментальная физика для студентов ВлГУ
 Скачать 7.12 Mb. Скачать 7.12 Mb.
|
|
Лекция 10. Уравнение Шреденгера. Задачи квантовой механики. План лекции: Стационарное уравнение Шредингера. Рассмотреть задачи квантовой механики: частица в «потенциальном ящике», туннельный эффект. Физика, изучающая (описывающая) вероятностное состояние микрообъектов, называется- квантовая механика. Одним из основоположников квантовой механики явился Э. Шреденгер, записавший основное уравнение, определяющее поведение микрообъектов, которое называется уравненим Шредингера. Это закон, описывающий изменение состояния микрообъектов. Из гипотезы де Бройля следовало, что всякому свободному движению частицы сопутствует некоторый волновой процесс, описание которого осуществляется с помощью волнового уравнения (см. курс электродинамики) или волновой функции, как решения этого уравнения. В простейшем случае (плоской волны) можно записать волновое уравнение в виде 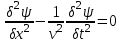 , где , где 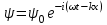 волновая функция. Рассматривая стационарное движение волны, мы можем, избавиться от переменной t . волновая функция. Рассматривая стационарное движение волны, мы можем, избавиться от переменной t . Действительно, если 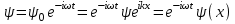 , то после подстановки в уравнение величины , то после подстановки в уравнение величины 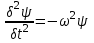 , получим: , получим: 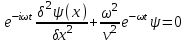 , откуда следует: , откуда следует: 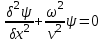 . Вычислим . Вычислим 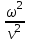 , используя гипотезу де Бройля , используя гипотезу де Бройля 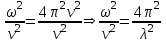 , но , но 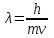 , тогда , тогда 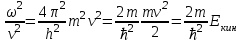 . .Уравнение волны де Бройля запишется следующим образом . 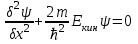 . .Если частица взаимодействует с полем и потенциальная энергия этого взаимодействия равна U, то 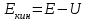 , где Е - полная энергия частицы. Тогда , где Е - полная энергия частицы. Тогда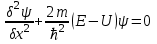 , где E- полная энергия микрообъекта, U- потенциальная энергия микрообъекта.что исторически представляет собой стационарное уравнение Шредингера. Решение уравнения Шреденгера позволяет найти , где E- полная энергия микрообъекта, U- потенциальная энергия микрообъекта.что исторически представляет собой стационарное уравнение Шредингера. Решение уравнения Шреденгера позволяет найти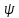 -функцию состояния микрообъекта, следовательно: -функцию состояния микрообъекта, следовательно:определяем вероятность обнаружения микрообъекта в том или ином месте пространства; из уравнения Шреденгера вытекает правило квантования энергии микрообъекта. Уравнение Шреденгера является фундаментальным уравнением для описания поведения микрообъектов с учетом их волновых свойств. Уравнение Шреденгера в квантовой механике для микрообъектов- это аналог уравнений Ньютона в классической механике для макрообъектов. Применим уравнение Шредингера при решении задачи для микрообъекта в «бесконечно глубоком потенциальном ящике». 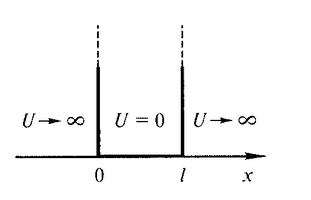 Условия: Условия: 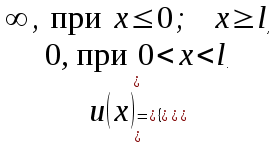 График потенциального "ящика" представлен на рисунке. Механическим аналогом является движение частицы между двумя абсолютно упругими стенками: взаимодействие "включается" только в точках x = 0 и x = l. Рассмотрим стационарное движение частицы, т.е. E (t) = const. Запишем уравнение Шредингера для области x ≤ 0, где U (x) = ∞: 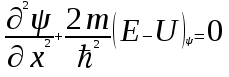 или или 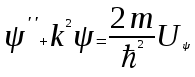 , или , или 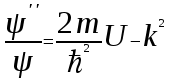 . Так как k ≠ ∞, то . Так как k ≠ ∞, то 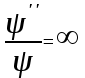 . Это возможно только тогда, когда ψ (x) = 0, а следовательно и | ψ (x) |2 = 0. Частицу нельзя обнаружить с координатой x ≤ 0. Аналогичные рассуждения приводят к тому, что ψ (0) = 0 и ψ (l) = 0. Таким образом мы определили граничные значения волновой ψ – функции. . Это возможно только тогда, когда ψ (x) = 0, а следовательно и | ψ (x) |2 = 0. Частицу нельзя обнаружить с координатой x ≤ 0. Аналогичные рассуждения приводят к тому, что ψ (0) = 0 и ψ (l) = 0. Таким образом мы определили граничные значения волновой ψ – функции.Пусть теперь 0 < x < l, где U (x) = 0. Тогда уравнение Шредингера примет вид: 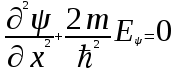 или или 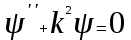 . .Решения такого уравнения уже известны: ψ (x) = Aeikx + Be-ikx (общее решение, как суперпозиция частных). Применим граничные условия ψ (x) = 0 при x = 0. Тогда A + B = 0, A = -B и ψ (x) = -B (coskx + isinkx) + + B (coskx - isinkx) = -2iBsinkx. При x = l, ψ (l) = 0, т.е. -2iBsinkl = 0. Это возможно, если В = 0 (в этом случае при всех x ψ (x) = 0 и объект не существует в пространстве) или sinkl = 0, что возможно при kl = nπ, т.е. 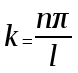 . .Вычислим энергию: 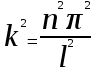 ; ; 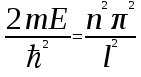 ; ; 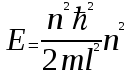 (n = 1, 2, …). Величина энергии оказалась "квантованной" и ее следует писать: (n = 1, 2, …). Величина энергии оказалась "квантованной" и ее следует писать: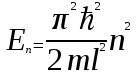 . Теперь вернемся к ψ – функции и вычислим константу "В" из условия нормировки: . Теперь вернемся к ψ – функции и вычислим константу "В" из условия нормировки: 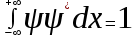 . . Тогда: 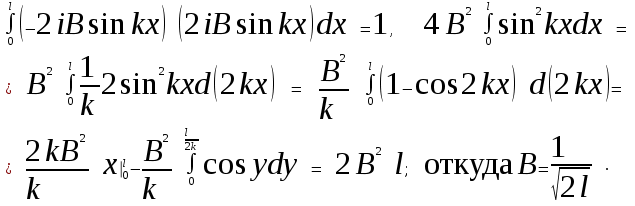 Окончательный вид решения можно записать следующим образом: 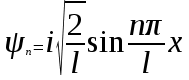 , , а функция плотности вероятности: 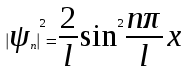 . .Изобразим полученное решение графически (рисунке). Большие квантовые числа приводят к тому, что функция плотности вероятности оказывается постоянной, что характерно для движения шарика между двумя упругими стенками (принцип соответствия). 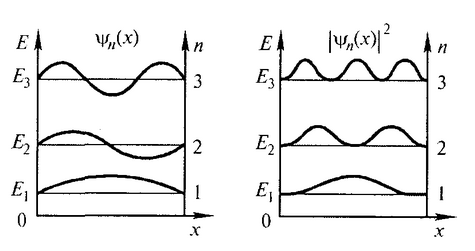 . .Практическое применение волны деБройля получили в электронографии и нейтронографии. Электронография - метод изучения структуры вещества, основанный на рассеянии ускоренных электронов исследуемым образцом. Применяется для изучения атомной структуры кристаллов, аморфных тел и жидкостей, молекул в газах и парах. Физическая основа электронографии. — дифракция электронов при прохождении через вещество электронов, обладающих волновыми свойствами. Дифракционная картина представлена на рисунке.  Электронография позволила изучать атомные структуры огромного числа веществ, существующих лишь в мелкокристаллическом состоянии. Она обладает преимуществом перед рентгеновским структурным анализом в определении положения лёгких атомов в присутствии тяжёлых. Нейтронография — метод изучения структуры вещества, основанный на дифракции нейтронов с энергией меньше 1 эВ; применяется для исследования структур водородсодержащих соединений. Рассеяние нейтронов происходит на ядрах атомов, что приводит к отсутствию систематической зависимости амплитуды рассеяния от порядкового номера химического элемента, в отличие от рассеяния электронов и рентгеновских лучей. Это позволяет использовать нейтронографию для определения положения атомов элементов-соседей в Периодической системе элементов. Методам нейтронографии доступны такие же исследования, но лишь для кристаллов значительно больших размеров, чем для исследуемых в электронографии и рентгенографии. Волновые свойства электронов используются в электронных микроскопах. Принципиальная схема микроскопа и внешний вид современного электронного микроскопа представлены на рисунке. Электронные микроскопы используются, в частности, для получения изображения поверхностей материалов на микро- и наноуровне. На рисунке представлена поверхность пористого анодированного оксида алюминия, указаны размеры пор. 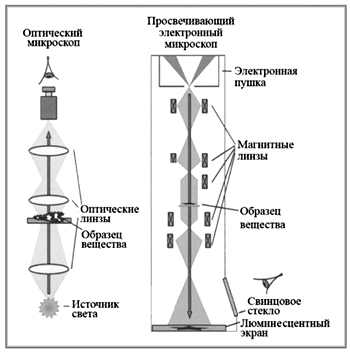  Электронный микроскоп в ВлГУ.  Лекция 11. Атомная физика. Боровская теория строения атома. План лекции: Первые модели строения атома. Опыт Резерфорда. Теория Бора. Д 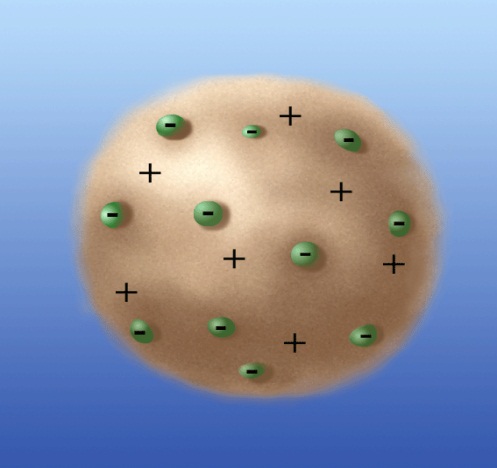 о конца XIX века в науке господствовало мнение, что вещества состоят из простейших частиц – атомов (неделимый). В конце XIX века в физике был получен ряд экспериментальных фактов, которые говорили о том, что атом имеет сложное строение: изучаются разряды в газах, были получены катодные лучи, которые представляют собой поток электронов, то есть, изучая катодные лучи физики получили мельчайшие отрицательно заряженные частицы, которые позже назвали электронами. о конца XIX века в науке господствовало мнение, что вещества состоят из простейших частиц – атомов (неделимый). В конце XIX века в физике был получен ряд экспериментальных фактов, которые говорили о том, что атом имеет сложное строение: изучаются разряды в газах, были получены катодные лучи, которые представляют собой поток электронов, то есть, изучая катодные лучи физики получили мельчайшие отрицательно заряженные частицы, которые позже назвали электронами.Был измерен удельный заряд 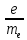 , масса , масса 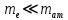 . Можно было предположить, что эти частицы входят в состав атома, но так как они заряжены, а атом нейтрален, следует, что в состав атома входят и положительно заряженные частицы. В конце XIX века изучаются спектры излучения атомов. Большая группа швейцарских физиков получили, что атомы излучают линейчатый спектр, причем атомы разных химических элементов дают разные спектры. Это говорит о том, что атом это сложная структура и что для каждого химического элемента своя структура атома. Исходя из имеющихся данных, были предложены модели атомов. Одной из первых моделей была предложена Томсоном (см.рисунок): атом представляет собой положительно заряженную сферу, в которую вкраплены отрицательно заряженные электроны. . Можно было предположить, что эти частицы входят в состав атома, но так как они заряжены, а атом нейтрален, следует, что в состав атома входят и положительно заряженные частицы. В конце XIX века изучаются спектры излучения атомов. Большая группа швейцарских физиков получили, что атомы излучают линейчатый спектр, причем атомы разных химических элементов дают разные спектры. Это говорит о том, что атом это сложная структура и что для каждого химического элемента своя структура атома. Исходя из имеющихся данных, были предложены модели атомов. Одной из первых моделей была предложена Томсоном (см.рисунок): атом представляет собой положительно заряженную сферу, в которую вкраплены отрицательно заряженные электроны. Рассмотрим атом водорода H (Z=1) (см. рисунок):   + модель Томсона статична, а в соответствии с теорией  - Максвелла, излучать может только движущаяся частица.   Атом статичен, а чтобы он излучал, его надо возбудить, то есть вывести из состояния равновесия, приложив квазиупругую силу: F=-kx. Смещая электрон под действием внешней силы из состояния равновесия, получают диполь. Такой гармонический осциллятор излучает частоты ω0, 2ω0, 3ω0. Спектр такого излучения не удовлетворяет опыту. Следовательно, принять такую модель нельзя. Атом статичен, а чтобы он излучал, его надо возбудить, то есть вывести из состояния равновесия, приложив квазиупругую силу: F=-kx. Смещая электрон под действием внешней силы из состояния равновесия, получают диполь. Такой гармонический осциллятор излучает частоты ω0, 2ω0, 3ω0. Спектр такого излучения не удовлетворяет опыту. Следовательно, принять такую модель нельзя.Одним из учеников Томсона был Резерфорд, который экспериментально проверял правильность модели атома по Томсону. В 1910-11 годах Резерфорд с учениками ставит опыт по проверке атома Томсона. Суть эксперимента: бомбардировка тяжелыми α-частицами металлической фольги. 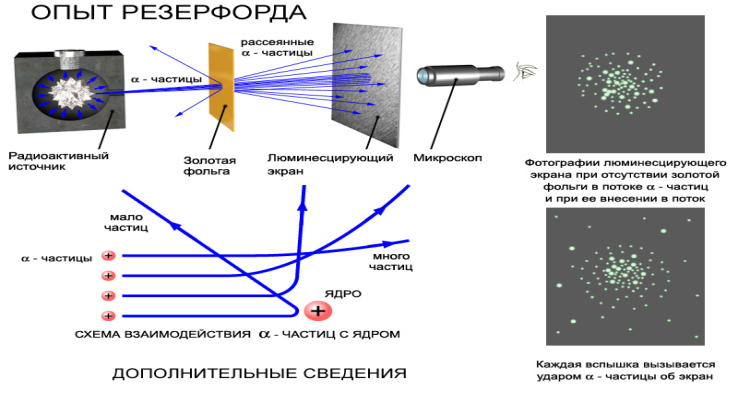 Если допустить, что атомы устроены по Томсону, то ожидалось получить, что α-частицы не будут резко менять траекторию, потому что легкие электроны не могут менять траекторию тяжелых α-частиц. Однако получили, что большая доля α-частиц не изменяют траекторию, но небольшая часть α-частиц резко изменяют траекторию движения, отклоняясь на угол >90 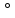 . Анализы экспериментов позволили Резерфорду высказать идею и предложить планетарную (ядерную) модель строения атома. Это значит, что изменить траекторию α-частиц может только: тяжелая, положительно заряженная частица, сосредоточенная в малом объеме. . Анализы экспериментов позволили Резерфорду высказать идею и предложить планетарную (ядерную) модель строения атома. Это значит, что изменить траекторию α-частиц может только: тяжелая, положительно заряженная частица, сосредоточенная в малом объеме.Эти эксперименты позволили предположить, что в центре атома находится атомное ядро. Вся масса атома сосредоточена в ядре, а вблизи ядра распределены электроны, движущиеся по круговым орбитам. Модель Резерфорда-шаг вперед по сравнению с моделью Томсона, так как она динамическая. Попробуем объяснить линейчатый спектр излучения атома с помощью модели Резерфорда. На электрон в атоме H действует кулоновская сила, которая создает центростремительное ускорение. II закон Ньютона: F=ma ; 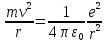 ; ; 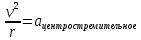 Резерфорд не накладывает никаких ограничений на величины 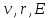 , то есть они могут принимать любые значения. Из II закон Ньютона можно выразить скорость электрона: , то есть они могут принимать любые значения. Из II закон Ньютона можно выразить скорость электрона: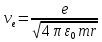 . Полная энергия складывается из кинетической и потенциальной . Полная энергия складывается из кинетической и потенциальной Eполн= Екин + Епот , или Еполн= 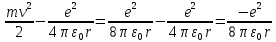 . Тогда . Тогда Еполн 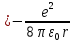 - по Резерфорду. - по Резерфорду.Полная энергия электрона в атоме может принимать любые значения, а, следовательно, атом излучает любые значения энергии, то есть спектр излучения атома сплошной, а опыт показывает, что атом дает линейчатый спектр. Таким образом, теория Резерфорда не объясняет линейчатый спектр излучения атома и не может объяснить устойчивость атома. По теории Максвелла непрерывно движущийся электрон в атоме должен постоянно излучать энергию, то есть энергия электрона уменьшается, траектория движения уменьшается и, в конце концов, электрон упадет на ядро. Опыт показывает, что атом в реальности устойчив. Дальнейшие работы по созданию теории строения атома принадлежат Н.Бору. Основные идеи Бор сформулировал в виде постулатов, в основу которых им были положены опытные факты: атомы - устойчивые системы; атомы излучают энергию порциями. Бор делает выводы из работ Планка, что энергия атома не может меняться непрерывно. Следовательно, должны существовать стационарные состояния атома, которые образуют дискретный ряд Е1, Е2, Е3,… - разрешенных энергетических состояний. 1 постулат: в атоме существует ряд стационарных устойчивых орбит, обращаясь по которым, электрон не излучает и не поглощает энергию. Современная трактовка: атом может находиться в ряде стационарных энергетических состояний без излучения и поглощения энергии. 2 постулат: излучение (поглощение) энергии происходит при переходе атома из одного разрешенного состояния, в другое 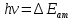 Энергия кванта излучения равна изменению энергии атома: 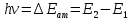 3 постулат: на разрешенных орбитах момент количества движения электрона кратен целому числу 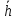 . .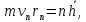 n=1,2,3,…, где n- квантовое число. n=1,2,3,…, где n- квантовое число.На современном языке последнее равенство является правилом квантования момента импульса электрона. Постулаты Бора не совместимы с классической физикой. Рассчитаем параметры атома водорода по Бору, Запишем основные законы для движущегося электрона в атоме водорода (Z=1). II закон Ньютона: 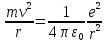 - условие устойчивости орбиты. - условие устойчивости орбиты.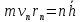 - правило квантования момента импульса. - правило квантования момента импульса.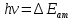 – закон сохранения и превращения энергии излучения атома. – закон сохранения и превращения энергии излучения атома.Из 1 и 2 получаем: 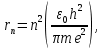 n=1,2,3… n=1,2,3… 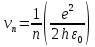 И 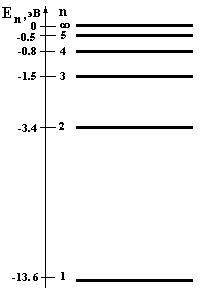 з уравнений следует, что и r и vменяются дискретно (зависят от квантового числа n). Eполн=Екин + Епот , Eполн= з уравнений следует, что и r и vменяются дискретно (зависят от квантового числа n). Eполн=Екин + Епот , Eполн=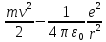 , Eполн= , Eполн=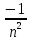 ( (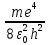 ) , n = 1,2,3,…. Знак минус в значении энергии показывает, что электрон в атоме связан. Из последней формулы для полной энергии видно, что энергия атома квантована (принимает набор возможных значений), в зависимости от квантового числа n. Энергетическая диаграмма атома водорода представлена на рисунке. ) , n = 1,2,3,…. Знак минус в значении энергии показывает, что электрон в атоме связан. Из последней формулы для полной энергии видно, что энергия атома квантована (принимает набор возможных значений), в зависимости от квантового числа n. Энергетическая диаграмма атома водорода представлена на рисунке.E∞=0 – max (максимальное значение энергии) E1 – min (минимальное значение энергии). En= 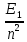 . .При больших n квантование энергии дает результаты близкие к классической физике. В этом находит выражение принцип соответствия Бора(1923г): при больших n выводы и результаты квантовой механики соответствуют классическим результатам. Состояние Е1 при n=1- устойчивое состояние атома (невозбужденное состояние). Все состояния с n>1 – возбужденные состояния атома. Исходя из постулатов Бора, атом может находиться в определенных энергетических состояниях. При переходе атома из одного энергетического состояния в другое, атом излучает или поглощает энергию в соответствии с законом сохранения и превращения энергии. Излучение: Ен>Ек; 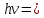 Ен‒Ек Ен‒Ек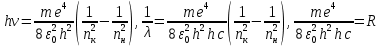 - постоянная Ридберга: - постоянная Ридберга:R=1,097·107м-1 . 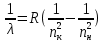 –спектр излучения атома линейчатый. –спектр излучения атома линейчатый. Выводы: теория атома H, созданная в 1913 году Бором, количественно и качественно согласуется с опытом: постулаты Бора позволяют объяснить закономерности водородного спектра; теория Бора объясняет структуру спектра водородоподобных ионов; теория позволяет вычислить постоянную Ридберга; объясняет природу характеристических рентгеновских спектров; объясняет расщепление спектральных линий в сильном магнитном поле (эффект Зеемана). Теория Бора проста для понимания. Она сыграла огромную роль в создании атомной физики, атомной и молекулярной спектроскопии. Затруднения Боровской теории Боровская теория- внутренне противоречивая теория, так как наряду с законами классической физики используется условие квантования момента импульса. Она явилась переходной от классической к современной (квантовой) теории. Ее называют полуклассической теорией: теория Бора не объясняет спектры сложных атомов (с числом электронов >1); не объясняет последовательность переходов атомов из одного состояния в другое; не объясняет предпочтения одних переходов перед другими; не объясняет взаимодействие атомов. |
