Курс лекций по основам численного расчета на прочность в программном комплексе abaqus 4 сае жуковский, 2003
 Скачать 0.79 Mb.
|
 Крылов Я. В.Курс лекций по основам численного расчета на прочность в программном комплексе ABAQUS 6.4 / САЕ Жуковский, 2003 Содержание Введение. ………………………………………………………………...3 Лекция 1. Структура САЕ-интерфейса. Моделирование статической линейной задачи для двумерного объекта на примере консольно закрепленной балки . ………………..……….4 Лекция 2. Моделирование статической линейной задачи для трехмерного объекта на примере изгиба консольно закрепленной балки. Использование различных типов элементов. Изменение параметров сетки. ………………………. 20 Лекция 3. Моделирование различных типов материалов (изотропные, ортотропные, слоистые, гиперэластичные) на примере изгиба консольно закрепленной балки. Задание пределов пропорциональности и прочности, переход к нелинейной статической задаче. …………………………………..24 Лекция 4. Моделирование динамической задачи на примере свободных колебаний консольно закрепленной балки. Анализ частотных характеристик, запись результатов анализа в отчетные файлы. ……………………………………………………...29 Лекция 5. Моделирование контактной задачи на примере падения твердого шара на свободный конец консольно закрепленной балки с различными начальными условиями. ...32 Лекция 6. Моделирование контактной задачи на примере взаимодействия консольно закрепленной балки и лежащего на ней упругого цилиндра, нагруженного поперечной силой. Запись результатов анализа в видеоклип. ………………………...40 Лекция 7. Моделирование статической линейной задачи на примере нагрева и охлаждения консольно закрепленной балки. Исследование возникающих температурных изменений. ….....44 Лекция 8. Моделирование статической линейной задачи на примере электростатического взаимодействия консольно закрепленной балки с заряженными телами различной геометрической формы. ……………………………………………..46 ФАЛТ МФТИ, ТЕСИС Введение. В настоящее время в связи с развитием электронно-вычислительной техники возрастает популярность конечно-элементных методов. Их преимущества состоят в том, что они позволяют достаточно точно и наглядно моделировать реальные конструкции, не прибегая к упрощениям и схематизации, как это происходит при аналитическом решении, и при этом довольно просты и удобны в работе. Программный комплекс ABAQUS является одним из наиболее мощных пакетов, базирующихся на МКЭ. Он хорошо зарекомендовал себя за рубежом и относится к классу “hi-end” САЕ-пакетов, удовлетворяющих стандартам, установленным Американской Ядерной Контрольной Комиссией. К сожалению, в нашей стране он пока не слишком распространен, поэтому объем русскоязычной литературы для ABAQUS не так велик, как хотелось бы. В частности, для студента технического вуза, обращающегося к МКЭ, профессиональное обучение слишком дорого, а самообучение этому программному комплексу длительно и неудобно, внутренняя документация для ABAQUS написана в виде текстового редактора файлов исходных данных и не описывает работу с графическим САЕ-препроцессором, не говоря уже о том, что многие полезные свойства и возможности этого комплекса для человека, изучающего ABAQUS самостоятельно, без специальной литературы, останутся в тени. Данный курс лекций – семестровый, рассчитан на студентов российских технических вузов и позволяет в сжатые сроки освоить основные приемы работы с ABAQUS 6.4 /САЕ. В конце курса приведены тестовые задачи для самостоятельного решения, которые могут быть использованы как преподавателем при зачете, так и студентом, использующим этот курс в качестве самоучителя для проверки полученных знаний. Лекция 1. Структура САЕ-интерфейса. Моделирование статической линейной задачи для двумерного объекта на примере консольно закрепленной балки. Запустите ABAQUS 6.4/CAE. В появившемся диалоговом окне StartSession, показанном на рисунке 1.1, предлагаются 4 возможных действия: Рисунок 1.1. 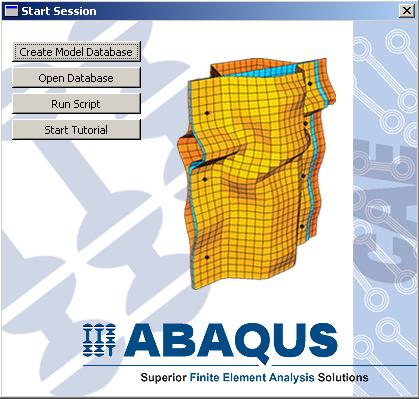 CreateModelDataBase – создание новой базы данных для модели; OpenDataBase – открытие существующей базы данных; RunScript– запуск сценария с заранее записанными командами; StartTutorial– запуск программы с документацией по обучению и создание новой базы данных. Выберите CreateModelDataBaseдля начала работы. Заголовок Панель меню Панель инструментов Панель состояния 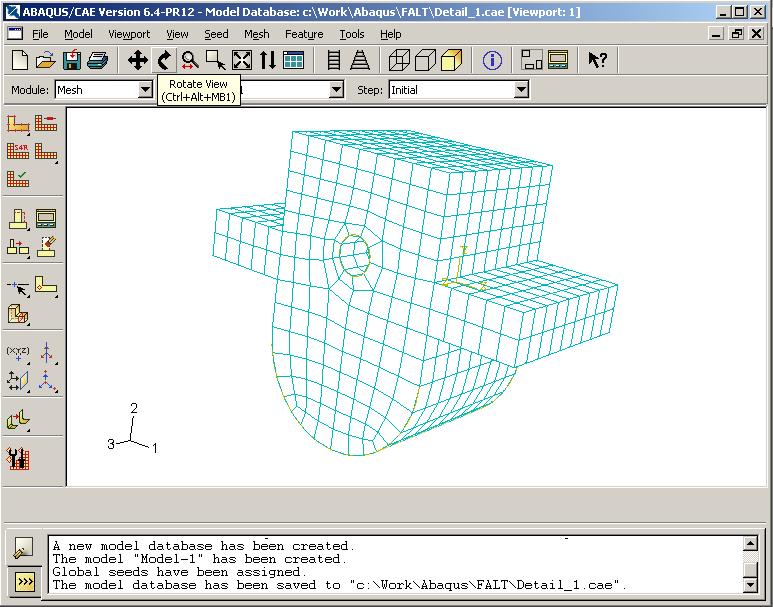 Текущая панель Окно просмотра Панель Окно компонент модулей моделей инструкций сообщений Рисунок 1.2. Перед Вами – рабочее пространство ABAQUS 6.4. Верхняя панель – панель меню, ниже ее – панель инструментов, под ней – панель состояния. В центре – рабочее окно просмотра моделей Viewport, слева от него – текущая панель компонент модулей, под ним – панель инструкций и окно сообщений. Все это составляет графический интерфейс САЕ, который изображен на рисунке 1.2. Размеры окна Viewportмогут меняться, но общий вид всех панелей и их расположение неизменно. Одной из особенностей ABAQUS является использование модулей, каждый из которых содержит некоторый набор действий, близких по значению и необходимых для построения конечно-элементной модели и дальнейших операций с ней. Это упрощает и делает более наглядной работу в ABAQUS. Для выбора модуля в левой части панели основных компонент есть ниспадающий список Module, показанный на рисунке 1.3. В нем представлены следующие модули: 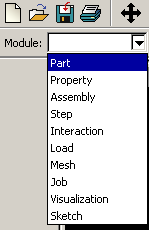 Рисунок 1.3. PART – модуль, предназначенный для создания деталей, задания их геометрии, опорных точек и систем координат; PROPERTY– модуль, предназначенный для определения материалов и сечений, применяемых в модели, а также для задания их физических характеристик; ASSEMBLY– модуль, предназначенный для задания взаимного расположения деталей и сборки их в целую модель; STEP– модуль, предназначенный для создания шагов расчета и определения выходных данных по результатам; INTERACTION– модуль, предназначенный для определения взаимодействий между деталями, контактных участков и их свойств; LOAD– модуль, предназначенный для создания нагрузок, прикладываемых к модели, а также начальных и граничных условий для нее; MESH– модуль, предназначенный для построения сетки, фактически, в нем происходит преобразование геометрической модели в конечно-элементную; JOB– модуль, предназначенный для создания файла выходных данных, проверки построенной модели, запуска вычислительного процесса и контроля над ним; VISUALISATION– модуль, предназначенный для просмотра результатов расчета и обработки полученных данных; SCETCH– модуль, предназначенный для сохранения эскизов и чертежей полученной модели. Рассмотрим консольно заделанную линейную балку длиной 10 см, прямоугольного сечения 5,0*1,0 мм2, изготовленную из дюралюминия Д16Т и подвергающуюся воздействию сосредоточенной силы величиной в 1 кН, приложенной к свободному концу. Ее общая схема представлена на рисунке 1.4. Теоретически, максимальный прогиб балки будет наблюдаться в точке приложения силы и составит = PL3/3EI, где I = аb3/12, а и b, соответственно, стороны сечения. P F L Рисунок 1.4. Для нашего случая = 1,4 мм. Согласно решению этой задачи в сопротивлении материалов эпюры перерезывающих сил Qу и моментов Мz имеют вид, представленный на рисунке 1.5. Q0 M0 Рисунок 1.5. Здесь Qо = P, Мо = PL.  Откройте в списке Module модуль PART. Для создания детали нажмите кнопкуCreatePart. Также, альтернативно, вы можете воспользоваться командой Part – Create на панели меню. Как правило, команды, вызываемые посредством панели меню, продублированы кнопками на панели текущих компонент модулей. На рисунке 1.6 показано окно CreatePart, возникающее в результате этой команды. Построим двумерную модель балки. Для этого в окне CreatePartзададим свойства так, как показано на рисунке, то есть создадим двумерную деформируемую кривую с максимальным размером области построения, равным 400 мм, и присвоим ей какое-нибудь имя, например, Beam-1. Подтвердим так заданные свойства нажатием кнопки Continue. На экране появится сетка, сопровождающая построение модели. Ее шаг по умолчанию равен 10 мм. С ее помощью построим прямую линию длиной 100 мм. Для ее построения нажмем кнопку CreateLinesConnected. 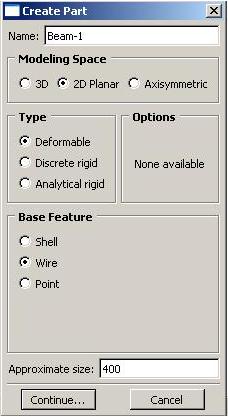  Теперь, двигаясь по узлам сетки, нарисуем линию требуемой длины. Можно также задать 2 точки в возникшем внизу окне, как это показано на рисунке 1.7, с координатами 0,0 и 100,0 и подтвердить свой выбор клавишей Enter. В случае ошибки можно произвести отмену действия при помощи кнопки  Cancel. Рисунок 1.6. Чтобы завершить геометрические построения, нажмите Сancel и возникающую внизу на панели инструкций кнопку Done. Для возврата к предыдущему действию служит находящаяся слева от кнопки CancelкнопкаBack.  Рисунок 1.7. 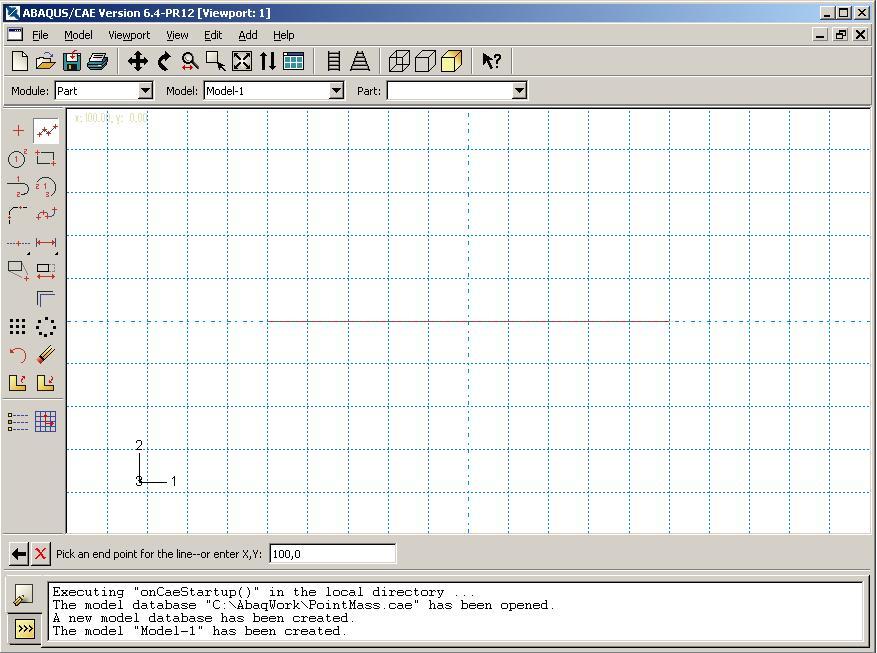 Перейдите к следующему модулю PROPERTY. Задайте материал балки, пользуясь кнопкой  CreateMaterial, либо командами меню Material -- Create. Возникнет окно EditMaterial, показанное на рисунке 1.8. В его верхней части указываются различные опции, из которых задайте только две: General – Density = 2600 кг/м3, и Mechanical – Elasticity – Elastic: Young’s Modulus = 5.6e+08 Па, Poisson’sRatio= 0.3. Присвойте материалу какое-нибудь имя, например, Duralumine, и подтвердите ввод нажатием кнопки ОК. Материал создан. Но это еще не значит, что балка приобрела его заданные свойства. Теперь необходимо создать сечение балки, приписать ему заданный материал и только потом присвоить это сечение всей балке. Для этого нажмите кнопку CreateProfile  либо воспользуйтесь командами меню Profile - Create. Появится окно CreateProfile, в котором надо выбрать профиль сечения. В ABAQUS есть набор уже готовых типов профилей. В нашем случае выберите прямоугольник путем использования командShape – Rectangular - Continue. В окне EditProfile, показанном на рисунке 1.9, задайте размеры сторон сечения, присвойте профилю какое-нибудь имя, по умолчанию – Profile-1. Подтвердите ввод кнопкой ОК и создайте само сечение с помощью кнопки CreateSectionили команд меню Section – Create. Рисунок 1.8 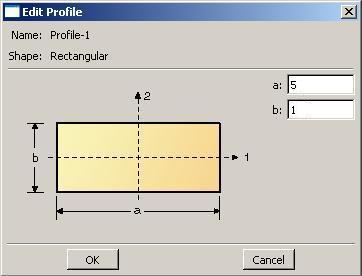 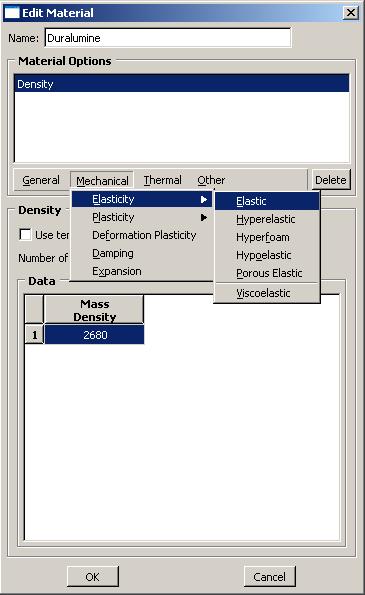  Выберите категорию детали, для которой определяется сечение, как Beam (балка), и тип самого сечения – тоже Beam, как это показано на рисунке 1.10. Присвойте сечению какое-нибудь имя, Рисунок 1.9. по умолчанию – Section-1. Нажатием кнопки Continue перейдите к окну редакции свойств сечения EditBeamSection и задайте их так, как показано на рисунке 1.11. Линейные свойства балки задайте в окнеBeamLinearBehavior, возникающем при нажатии кнопки LinearProperties. В общем случае вам потребуется вычислить модуль сдвига по известной формуле G = E/2(1+), где – коэффициент Пуассона, и указать его в окне ShearModulus. Также можете задать начальную температуру Рисунок 1.10. 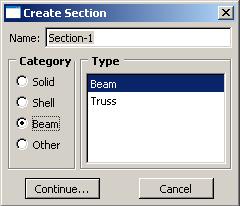 Reference Temperature, однако в нашем случае это не обязательно. Остальные свойства сечения задаются аналогично случаю определения свойств материала. По умолчанию берутся те же свойства, какими обладает уже созданный материал, так что в нашем случае не обязательно заполнять все графы. Подтвердите ввод свойств сечения Рисунок 1.11. 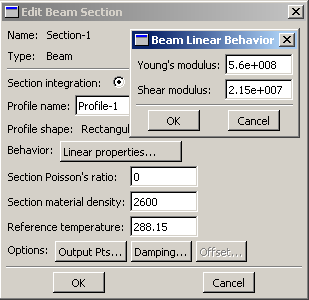 с помощью кнопки ОК. Теперь присвойте построенное таким образом сечение созданной в предыдущем модуле балке. Для этого используйте кнопку AssignSectionлибо команды меню Assign – Section. С помощью мыши укажите на балку, она будет выделена красным цветом. В предложенном списке выберите сечение, оно всего одно, и подтвердите выбор нажатием кнопки ОК.  Осталось только определить, как направлены сечения внутри балки. Для этого нажмите кнопку AssignSection Orientationлибо используйте команду меню Assign – BeamSection Orientation. С помощью мыши укажите на балку, она будет выделена красным цветом, и подтвердите выбор нажатием кнопки Done. На панели инструкций возникнет окно, в котором вам надо задать направление вектора вдоль оси «Х» (стороны а) сечения. Введите числа 0.0, 1.0, 0.0 и, убедившись в правильности направления сечений, нажмите кнопку ОК.  Перейдите к модулю ASSEMBLY. В нем надо создать сборку имеющихся деталей. Поскольку в нашем случае всего одна деталь, балка, достаточно нажать кнопку CreatePartInstance либо воспользоваться командами меню Instance – Create. Возникнет окно со списком готовых деталей Parts. В нашем случае деталь всего одна, выберем ее – она будет выделена красным цветом, и подтвердим выбор – цвет, обозначающий сборку, изменится на синий.  Теперь надо задать шаг расчета. Поскольку ABAQUS представляет собой пакет программ и использует разные решатели в зависимости от постановки задачи, необходимо определить, каким именно решателем мы будем пользоваться. Перейдите к модулю STEPи создайте шаг расчета с помощью кнопки CreateStep  либо команд меню Step – Create. Возникнет окноCreateStep, в котором уже указан начальный шаг расчета Initial. Задайте следующий шаг Static, Generalи присвойте ему какое-нибудь имя, по умолчанию – Step-1. Нажав на кнопку Continue, вызовите окно редакции шага расчета EditStep, показанное на рисунке 1.12. В графе Descriptionукажите тип решаемой задачи, например, ConsoleBeam. Активируйте опцию нелинейного анализа, указав Nlgeom=On, как на рисунке, и нажмите OK. Рисунок 1.12. 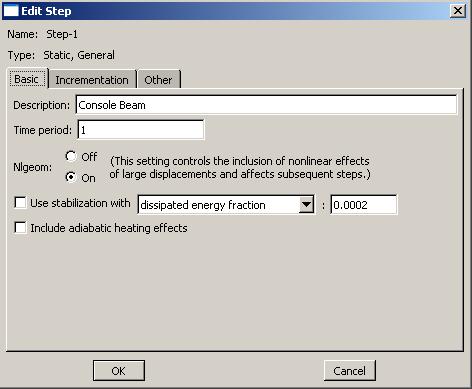 В модуле STEP есть еще 2 важные кнопки, CreateFieldOutput  иCreate HistoryOutput  .Они позволяют задавать переменные, которые надо определить в ходе расчета – напряжения, энергии, деформации и тому подобное. Часть из них задается автоматически. Просмотреть, как это сделано, а также внести соответствующие изменения можно с помощью так называемого менеджера – они есть в каждом модуле и вызываются одинаковыми кнопками.  Воспользуйтесь ей для FieldOutput либо командами меню Output – Field Requests – Manager. Появится окноFieldOutputRequestsManager, показанное на рисунке 1.13. Нажмите кнопкуEdit, чтобы выбрать необходимые выходные данные из списка. В этом менеджере, как и в любом другом, можно также создавать, изменять, копировать и удалять соответствующие компоненты текущего модуля. Выход из менеджера осуществите кнопкой Dismiss. 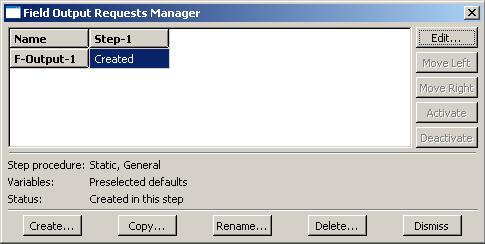 Рисунок 1.13. В нашей задаче нет взаимодействий, поэтому модуль INTERACTION опустим. Перейдите сразу к модулю LOAD. Задайте сосредоточенную силу, действующую на конец балки, с помощью кнопки CreateLoad  или команд меню Load – Create. Укажите шаг, на котором действует нагрузка (Step-1), присвойте ей какое-нибудь имя, по умолчанию – Load-1, определите категорию Categoryнагрузки Mechanical и тип нагружения TypesforSelectedStepкак сосредоточенная сила ConcentratedForce. Нажмите кнопку Continue и перейдите к следующему окну EditLoad. В нем укажите точку на конце балки, как показано на рисунке 1.14, и задайте величину сосредоточенной силы CF2 = -1000. Нажатием кнопки ОК подтвердите выбор. Нагрузка на балку задана. Граничные условия задайте аналогично, закрепив неподвижно другой, ненагруженный конец. Для этого используйте кнопку CreateBC либо команды меню BC – Create.  Рисунок 1.14. 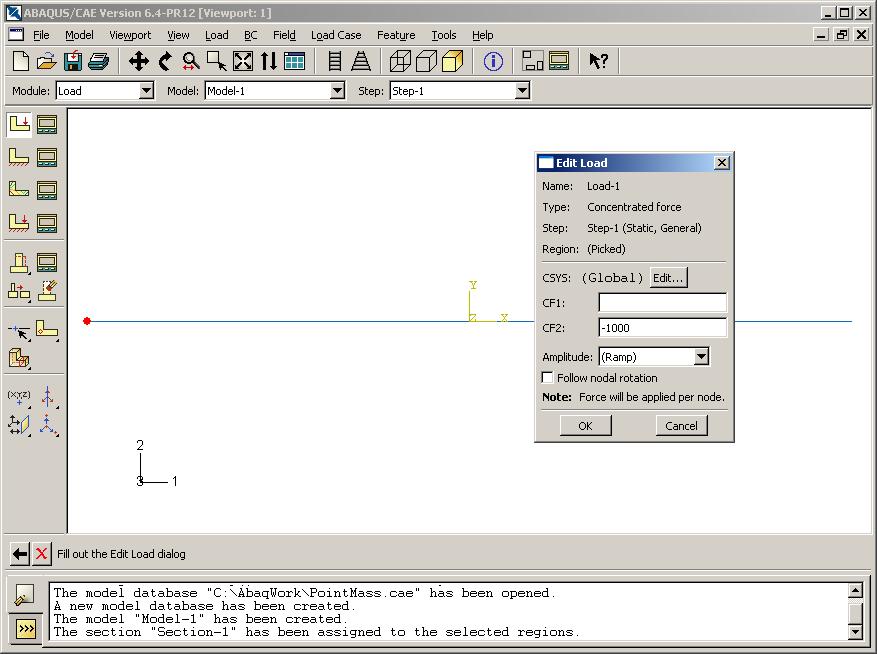 В появившемся окне CreateBoundaryConditionзадайте на шаге Initial категорию граничного условия Mechanical и его тип Symmetry/Antisymetry/Encastre. Присвойте заделке какое-нибудь имя, по умолчанию – BC-1. Укажите на свободный конец балки, подтвердите выбор и,нажав кнопку Continue, перейдите к следующему окну EditBoundaryCondition. В нем выберите последнюю графу Encastre, то есть нулевые линейные и угловые перемещения в указанной точке, и нажмите ОК. Теперь строим конечно-элементную сетку. Для этого перейдите в модуль MESH. Прежде, чем построить сетку, надо определить размеры элементов. С этой целью в ABAQUS используется опция Seed.  Нажмите на кнопку SeedPartInstance и продолжайте удерживать треугольную закладку в ее нижнем правом углу, пока не появится подменю, в которомвыберите кнопкуSeedEdgeByNumber либо воспользуйтесь командами меню Seed – EdgeByNumber. С помощью мыши выделите балку и в окне на панели инструкций задайте количество элементов вдоль нее, например, 10. Подтвердив ввод кнопкой Done, вы увидите на балке ряд окружностей, обозначающих предполагаемые положения узлов сетки. Можно также было задать размер элемента другими способами, например, кнопками SeedEdgeBySizeили SeedEdgeBiased.  Теперь надо определить, на основе каких элементов будет построена модель балки. Рисунок 1.15 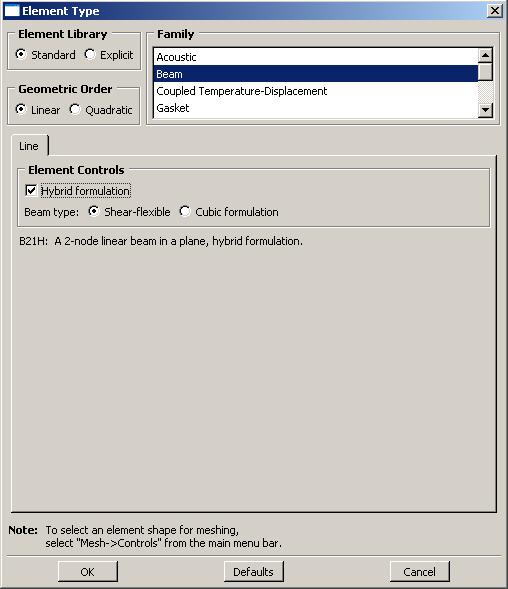 После нажатия кнопки Assign MeshControls или вызова команд меню Mesh – Controlsпоявляется окно, в котором надо указать категорию используемых элементов, для одномерных элементов это не нужно. Кнопка AssignElementTypeили команды менюMesh – ElementTypeвызывает окно, представленное на рисунке 1.15. Выберите тип элемента B21H, как это показано на рисунке, задав линейный порядок элемента, содержащегося в стандартной библиотеке, из разряда балочных, работающего на сдвиг в гибридной формулировке. Теперь, когда все готово для построения сетки, нажмите кнопку CreateMeshPartInstance или использовав команды меню Mesh – PartInstance – Create. Нажмите ОК, и балка покроется одномерной сеткой. Конечно-элементная модель готова.    Перейдите к модулю JOB. С помощью кнопки CreateJob либо команд меню Job – Create создайте файл данных с расширением *.odb, из которого после окончания расчета можно считать результаты. В появившемся окне CreateJob, которое показано на рисунке 1.16, присвойте этому файлу какое-нибудь имя, например, Beam2D-Bending. Имя надо задавать уникальным, это позволит избежать путаницы, когда у вас накопится много файлов *.odb. Для Рисунок 1.16. 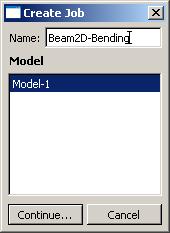  продолжения нажмите кнопку Continue и в окне EditJob, показанном на рисунке 1.17, задайте тип вычисления Full analisys, очередность выполнения Background и время на подтверждение Immediately. Можете также указать описание выполняемой работы, например, Bendingstatic, это особенно полезно, когда к модели прикладываются различные нагрузки, задаются разные граничные условия или есть несколько шагов расчета. Подтвердите ввод нажатем кнопки ОК. Вычислительный процесс сформирован. Чтоб запустить его, вызовите JobManagerсоответствующей кнопкой либо командами меню Job – Managerи нажмите на кнопку Submit. Рисунок 1.17. 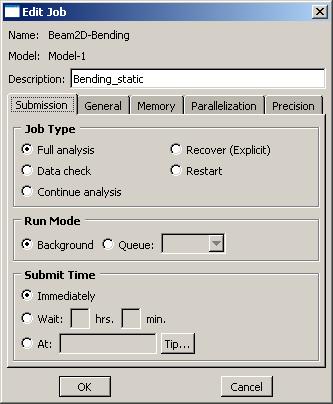 Надпись Runningговорит о работе процесса, когда она сменится на Completed - нажимайте кнопку Results, чтобы просмотреть результаты расчета. Вы автоматически перейдете в модуль VISUALISATION. КнопкаFastRepresentation  позволяетпросмотреть общий вид модели, кнопка PlotDeformed  показывает вид деформированной модели, кнопка PlotUndeformed возвращает исходную модель, кнопка PlotContour  отображает распределение по модели результирующей переменной, по умолчанию – напряжения по Мизесу, в виде цветовых градаций. Как обычно, все эти кнопки продублированы одноименными командами в меню Plot. Рисунок 1.18. 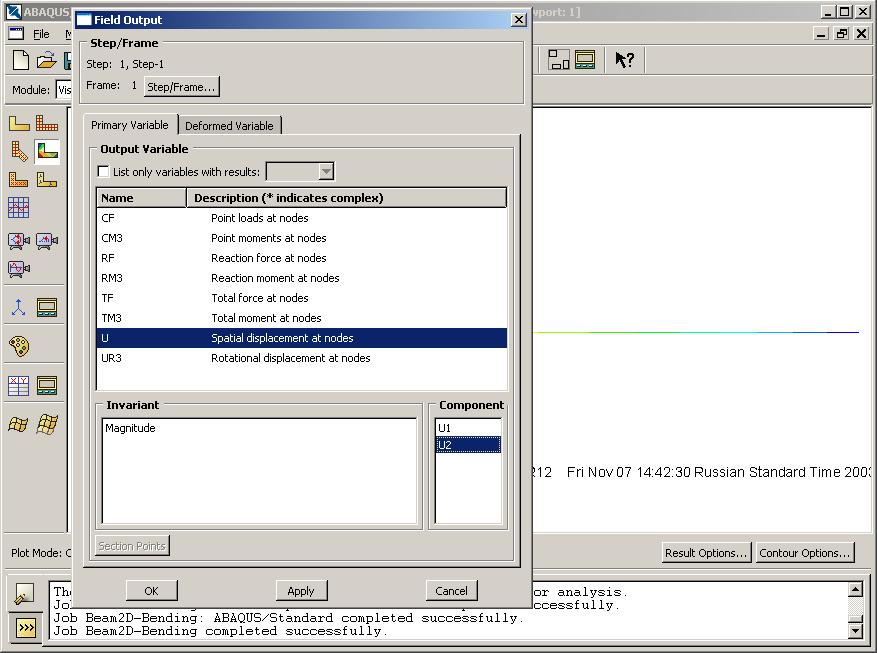 Можете заказать распределение любой переменной, используя команду меню Result – Field Output. В возникшем окне, показанном на рисунке 1.18, укажите интересующую вас переменную. Там же можно заказать переменную, определяющую экранную деформацию модели – она вовсе не обязательно должна совпадать с физической деформацией. Обратите внимание, что некоторые переменные состоят из нескольких компонент, и в списке внизу вы можете определить именно ту, которая вам нужна, учитывая оригинальную систему координат ABAQUS: X, Y и Z нумеруются, соответственно, 1, 2 и 3. Теперь сравните максимальную величину прогиба всей балки с ее расчетным значением. |