Статистика. Курс лекций по теории статистики
 Скачать 3.05 Mb. Скачать 3.05 Mb.
|
2.3. Принципы построения статистических группировок и классификацийПостроение группировки начинается с определения состава группировочных признаков. Группировочным признаком называется признак, по которому проводится разбиение единиц совокупности на отдельные группы. От правильного выбора группировочного признака зависят выводы статистического исследования. В качестве основания группировки необходимо использовать существенные, теоретически обоснованные признаки. В основание группировки могут быть положены как количественные, так и качественные признаки. Первые имеют числовое выражение (объем торгов, возраст человека, доход семьи и т. д.), а вторые отражают состояние единицы совокупности (пол, семейное положение, отраслевая принадлежность предприятия, его форма собственности и т. д.). После того, как определено основание группировки следует решить вопрос о количестве групп, на которые надо разбить исследуемую совокупность. Число групп зависит от задач исследования и вида показателя, положенного в основание группировки, объема совокупности, степени вариации признака. Например, группировка предприятий по формам собственности учитывает муниципальную, федеральную и собственность субъектов федерации. Если группировка производится по количественному признаку, то тогда необходимо обратить особое внимание на число единиц исследуемого объекта и степень колеблемости группировочного признака. При небольшом объеме совокупности не следует образовывать большого количества групп, так как группы будут включать недостаточное число единиц объекта. Поэтому показатели, рассчитанные для таких групп, не будут представительными и не позволят получить адекватную характеристику исследуемого явления. Часто группировка по количественному признаку имеет задачу отразить распределение единиц совокупности по этому признаку. В этом случае количество групп зависит, в первую очередь, от степени колеблемости группировочного признака: чем больше его колеблемость, тем больше можно образовать групп. Чем больше групп, тем точнее будет воспроизведен характер исследуемого объекта. Однако, слишком большое число групп затрудняет выявление закономерностей при исследовании социально-экономических явлений и процессов. Поэтому в каждом конкретном случае при определении числа групп следует исходить не только из степени колеблемости признака, но и из особенностей объекта и цели исследования. Определение числа групп можно осуществить и математическим путем с использованием формулы Стерджесса: n = 1 + 3,322 lg N, (2.1) где n - число групп N - число единиц совокупности. Согласно этой формуле выбор числа групп зависит от объема совокупности. Недостаток формулы состоит в том, что ее применение дает хорошие результаты, если совокупность состоит из большого числа единиц и если распределение единиц по признаку, положенному в основание группировки, близко к нормальному. Другой способ определения числа групп основан на применении показателя среднего квадратического отклонения (). Если величина интервала равна 0.5, то совокупность разбивается на 12 групп, а когда величина интервала равна 2/3 и , то совокупность делится, собственно, на 9 и 6 групп. Однако, при определении групп данными методами существует большая вероятность получения «пустых» или малочисленных групп. Когда определено число групп, то следует определить интервалы группировки. Интервал - это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей - наибольшее значение признака в интервале. Величина интервала представляет собой разность между верхней и нижней границами. Интервалы группировки в зависимости от их величины бывают: равные и неравные. Последние делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные. Если вариация признака проявляется в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами. Величина равного интервала определяется по следующей формуле: где хmax, xmin - максимальное и минимальное значения признака в совокупности; n -число групп. Если максимальные или минимальные значения сильно отличаются от смежных с ними значений вариантов в упорядоченном ряду значений группировочного признака, то для определения величины интервала следует использовать не максимальное или минимальное значения, а значения, несколько превышающие минимум, и несколько меньше, чем максимум. Полученную по формуле (2.2) величину округляют и она будет являться шагом интервала. Существуют следующие правила определения шага интервала. Если величина интервала, рассчитанная по формуле (2.2) представляет собой величину, которая имеет один знак до запятой (например: 0,88; 1,585; 4,8), то в этом случае полученные значения целесообразно округлить до десятых и их использовать в качестве шага интервала. В приведенном выше примере это будут соответственно значения: 0,9; 1,6; 4,7. Если рассчитанная величина интервала имеет две значащие цифры до запятой и несколько после запятой (например 15,985), то это значение необходимо округлить до целого числа (до 16). В случае, когда рассчитанная величина интервала представляет собой трехзначное, четырехзначное и так далее число, то эту величину следует округлить до ближайшего числа, кратного 100 или 50. Например, 557 следует округлить до 550 или до 600. Если размах вариации признака в совокупности велик и значения признака варьируют неравномерно, то надо использовать группировку с неравными интервалами. Неравные интервалы могут быть прогрессивно возрастающие или убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической и геометрической прогрессии определяются следующим образом: hi+1 = hi + a, а в геометрической прогрессии: hi+1 = hi q, где а - константа: для прогрессивно возрастающих интервалов имеет знак «+«, и знак «-» - при прогрессивно - убывающих; q - константа: больше «1» - для прогрессивно - возрастающих и меньше «1» - в другом случае. Применение неравных интервалов обусловлено тем, что в первых группах небольшая разница в показателях имеет большое значение, а в последних группах эта разница не существенна. Например, при построении группировки предприятий отрасли по показателю численности промышленно- производственного персонала, который варьирует от 200 человек до 2000 человек, нецелесообразно рассматривать равные интервалы, т. к. учитываются как малые, так и крупнейшие предприятия отрасли. Поэтому следует образовывать неравные интервалы: 200-500, 500-1100, 1100-2000, т. е. величина каждого последующего интервала больше предыдущего на 300 человек и увеличивается в арифметической прогрессии. Интервалы группировок могут быть закрытыми и открытыми. Закрытыми называются интервалы, у которых имеются верхняя и нижняя границы. Открытые - это те интервалы, у которых указана только одна граница: верхняя - у первого, нижняя - у последнего. Например, группы коммерческих банков по числу работающих в них сотрудников (чел.): до 200, 200-300, 300-400, 400 и более. При группировке единиц совокупности по количественному признаку границы интервалов могут быть обозначены по-разному, в зависимости от того, непрерывный это признак или дискретный. Если основанием группировки служит непрерывный признак (например, группы строительных фирм по объему работ (млн. руб.): 1200-1400, 1400-1600, 1600-1800, 1800-2000), то одно и то же значение признака выступает и верхней и нижней границами двух смежных интервалов. В данном случае объем работ 1400 млн. руб. составляет верхнюю границу первого интервала и нижнюю границу второго, 1600 млн. руб. - соответственно второго и третьего и т. д.,т. е. верхняя граница i - го интервала равна нижней границе (i+1) - го интервала. При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы объекта, значения признака у которых совпадают с границами интервалов. Например, во вторую или третью группу должна войти строительная фирма с объемом работ 1600 млн. рублей? Если верхняя граница формируется по принципу «исключительно», то фирма должна быть отнесена к третьей группе, в противном случае - ко второй. Для того, чтобы правильно отнести к той или иной группе единицу объекта, значение признака которой совпадает с границами интервалов, можно использовать открытые интервалы (по нашему примеру группы строительных фирм по объему работ преобразуются в следующие: до 1400, 1400-1600, 1600-1800, 1800 и более). В данном случае, вопрос отнесения отдельных единиц совокупности, значения которых являются граничными, к той или иной группе решается на основе анализа последнего открытого интервала. Возможны два случая обозначения последнего открытого интервала: 1).1800 млн. руб. и более; 2). более 1800 млн. руб. В первом случае, строительные фирмы с объемом работ 1600 млн. руб. попадут в третью группу; во втором случае - во вторую группу. Если в основании группировки лежит дискретный признак, то нижняя граница i-го интервала равна верхней границе i-1-го интервала, увеличенной на 1. Например, группы строительных фирм по числу занятого персонала (чел.) будут иметь вид: 100-150, 151-200, 201-300. При определении границ интервалов статистических группировок иногда исходят из того, что изменение количественного признака приводит к появлению нового качества. В этом случае граница интервала устанавливается там, где происходит переход от одного качества к другому. Строя такую группировку, следует дифференцированно устанавливать границы интервалов для разных отраслей народного хозяйства. Это достигается путем использования группировок со специализированными интервалами. Специализированные - это такие интервалы, которые применяются для выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях. При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно возрастающими, ни прогрессивно убывающими. Такие интервалы называются произвольными и, как правило, используются при группировке предприятий, например, по уровню рентабельности. Пример. Произведем анализ 30 самых надежных малых и средних банков РФ (на 1.04.96 г.) применяя метод группировок по следующим данным:
В качестве группировочного признака возьмем уставный фонд. Образуем четыре группы банков с равными интервалами. Величину интервала определим по формуле:  Обозначим границы групп: 2100-7350 - 1-я группа 7350-12600 - 2-я группа 12600-17850 - 3-я группа 17850-23100 - 4-я группа После того как определен группировочный признак - уставный фонд, задано число групп - 4 и образованы сами группы, необходимо отобрать показатели, которые характеризуют группы и определить их величины по каждой группе. Показатели, характеризующие банки, разносятся по четырем указанным группам и подсчитываются групповые итоги. Результаты группировки заносятся в таблицу и определяются общие итоги по совокупности единиц наблюдения по каждому показателю. Таблица 2.1 Группировка коммерческих банков по величине уставного фонда
Структурная группировка коммерческих банков на основе данных таблицы 2.1 будет иметь вид: Таблица 2.2 Группировка коммерческих банков по величине уставного фонда (в %% к итогу).
Из таблицы 2.2 видно, что в основном преобладают малые банки - 60%, на долю которых приходится 42,5% всего капитала. Более конкретный анализ взаимосвязи показателей можно сделать на основе аналитической группировки. Таблица 2.3 Группировка коммерческих банков по величине уставного фонда 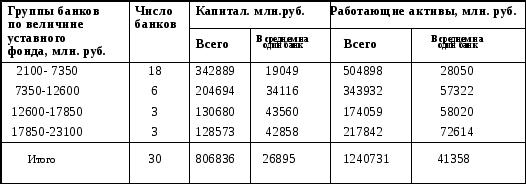 Величина капитала и работающие активы прямо зависят между собой и чем крупнее банк, тем эффективнее управление работающими активами. Мы рассмотрели примеры группировок по одному признаку. Однако в ряде случаев для решения поставленных задач такая группировка является недостаточной. В этих случаях переходят к группировке исследуемой совокупности по двум и более существенным признакам во взаимосвязи (комбинационной группировке). Произведем группировку данных коммерческих банков по двум признакам: величине капитала и работающим активам. Каждую группу и подгруппу охарактеризуем следующими показателями: число коммерческих банков, капитал, работающие активы. Таблица 2.4 Группировка коммерческих банков по величине капитала и работающим активам.
От группировок следует отличать классификацию. Классификацией называется систематизированное распределение явлений и объектов на определенные группы, классы, разряды на основании их сходства и различия. Отличительными чертами классификаций является то что: в основу их кладется качественный признак; они стандартны и устанавливаются органами государственной и международной статистики; они устойчивы, так как остаются неизменными в течение длительного периода времени. Ряды распределения представляют собой простейшую группировку, в которой каждая выделенная группа характеризуется одним показателем. Статистический ряд распределения - это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку. В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения. Атрибутивными называют ряды распределения, построенные по качественным признакам, то есть признакам, не имеющим числового выражения. Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволяют исследовать изменение структуры. Вариационными рядами называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами называются отдельные значения признака, которые он принимает в вариационном ряду, то есть конкретное значение варьирующего признака. Частотами называются численности отдельных вариант или каждой группы вариационного ряда, то есть это числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, ее объем. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%. В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды. Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Например, группы семей по числу детей (чел.): 1, 2, 3 и более. В случае непрерывной вариации величина признака у единиц совокупности может принимать в определенных пределах любые значения, отличающиеся друг от друга на сколь угодно малую величину. Построение интервальных вариационных рядов целесообразно прежде всего при непрерывной вариации признака, а также если дискретная вариация проявляется в широких пределах, то есть число вариантов дискретного признака достаточно велико. Правила построения рядов распределения аналогичны правилам построения группировки. Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения. Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот. Иногда для замыкания полигона предлагается крайние точки (слева и справа на ломаной линии) соединить с точками на оси абсцисс, в результате чего получается многоугольник. Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенным на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате мы получим график, на котором ряд распределения изображен в виде смежных друг с другом столбиков. Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми. При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение интервала и получения возможности сравнивать частоты. Плотность распределения - это частота, рассчитанная на единицу ширины интервала, то есть сколько единиц в каждой группе приходится на единицу величины интервала. Для графического изображения вариационных рядов может использоваться кумулятивная кривая. При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумуляту. Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву. |
