Статистика. Курс лекций по теории статистики

Название	Курс лекций по теории статистики
Анкор	Статистика
Дата	31.01.2022
Размер	3.05 Mb.
Формат файла
Имя файла	Teoria_statistikiLektsii.doc
Тип	Курс лекций #347192
страница	37 из 37

1 ... 29 30 31 32 33 34 35 36 37

12.3.Сводные индексы в средней арифметической и средней гармонической формах

В ряде случаев на практике вместо индексов в агрегатной форме удобнее использовать средние арифметические и средние гармонические индексы. Любой сводный индекс можно представить как среднюю взвешенную из индивидуальных индексов. Однако при этом форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу.

Предположим , мы располагаем данными о стоимости проданной продукции в текущем периоде и индивидуальными индексами цен, полученными, например, в результате выборочного наблюдения. Тогда при расчете сводного индекса цен можно использовать следующую замену:

В целом же сводный индекс цен в данном случае будет выражен в форме средней гармонической: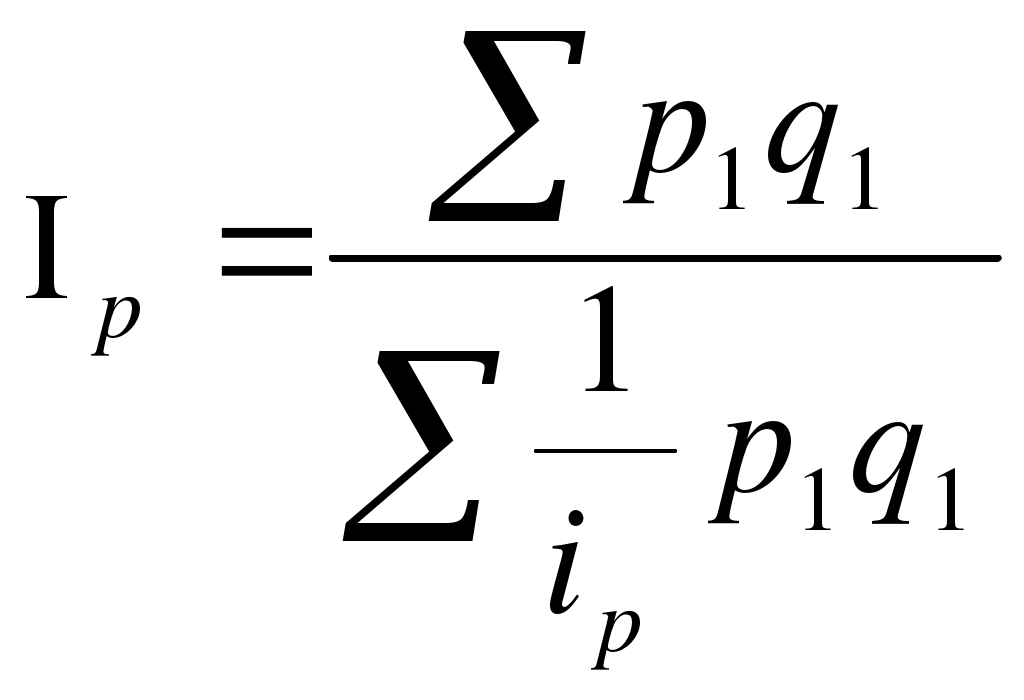

(11.8)

Рассмотрим следующий условный пример (табл. 11.2.):

Таблица 11.2
Данные о реализации и ценах по товарной группе

Т о в а р	Реализация в текущем периоде, руб.	Изменение цен в текущем периоде по сравнению с базисным,%
А	23000	+4,0
Б	21000	+2,3
В	29000	-0,8

Данные последней графы таблицы отражают изменение индивидуальных индексов цен, которые по товарам А, Б и В соответственно равны 1,040, 1,023 и 0,992.

С учетом этого получим:

Цены по данной товарной группе в среднем возросли на 1,6%.
При расчете сводного индекса физического объема товарооборота можно использовать среднеарифметическую форму. При этом производится замена:

Тогда индекс имеет вид:

(11.9)

Для иллюстрации этой формы расчета воспользуемся следующим примером (табл. 11.3.):

Таблица 11.3

Данные о реализации трех товаров в натуральном и стоимостном выражении

Т о в а р	Реализация в базисном периоде,руб.	Изменение физического объема реализации в текущем периоде по сравнению с базисным,%
А	46000	-6,4
Б	27000	-8,2
В	51000	+1,3

Индивидуальные индексы физического объема будут равны 0,936; 0,918; 1,013. С учетом этого рассчитаем среднеарифметический индекс:

Физический объем реализации данных товаров в среднем снизился на 3,6%.

12.4.Системы индексов

Индексы могут использоваться для анализа динамики социально-экономических явлений за ряд последовательных периодов. В этом случае для достижения сопоставимости они должны рассчитываться по единой схеме. Такая схема расчета индексов за несколько временных периодов называется системой индексов.

В зависимости от информационной базы и целей исследователя индексная система может строится в четырех вариантах. Рассмотрим их на примере сводного индекса цен, рассчитываемого за n периодов:
А. Цепные индексы цен с переменными весами:

. . . .

Б.Цепные индексы цен с постоянными весами:

. . . .

В. Базисные индексы цен с переменными весами:

. . . .

Г. Базисные индексы цен с постоянными весами:

. . . .

Индексы системы "Б" по своей природе мультипликативны, т.е. последовательное произведение этих индексов приводит к сводному индексу цен за весь рассматриваемый период (система "Г").

12.5.Индексы постоянного и переменного состава

В предыдущих задачах рассматривались индексы, рассчитываемые по нескольким товарам или видам продукции, реализуемым или производимым в одном месте. Рассмотрим теперь случай, когда один товар или вид продукции реализуется или производится в нескольких местах (табл. 11.4.):

Таблица 11.4
Реализация товара А в двух регионах

	Июнь		Июль
Регион	цена, руб.	продано, шт.	цена, руб.	продано,шт
1	12	10000	13	18000
2	17	20000	19	9000

Так как в данном случае реализуется один и тот же товар, вполне правомерно рассчитать его среднюю цену за июнь и за июль. Сравнением полученных средних значений получают индекс цен переменного состава:

(11.10)
Из таблицы видно, что цена в каждом регионе в июле по сравнению с июнем возросла. В целом же, средняя цена снизилась на 2,2%. Такое несоответствие объясняется влиянием изменения структуры реализации товаров по регионам: в июне по более высокой цене продали товара вдвое больше, в июле ситуация принципиально изменилась (в данном условном примере для наглядности числа подобраны таким образом, чтобы это различие в структуре продаж было очевидным). Оценить воздействие этого фактора можно с помощью индекса структурных сдвигов: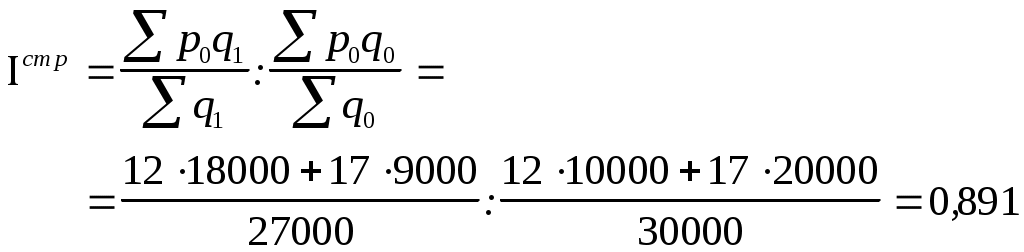

(11.11)
Первая формула в этом индексе позволяет ответить на вопрос, какой была бы средняя цена в июле, если бы цены в каждом регионе сохранились на прежнем июньском уровне. Вторая часть формулы отражает фактическую среднюю цену июня. В целом по полученному значению индекса мы можем сделать вывод, что за счет структурных сдвигов цены снизились на 10,9%.
Последним в данной системе является рассмотренный выше индекс цен фиксированного состава, который не учитывает влияние структуры:

(11.12).
Итак, если бы структура реализации товара А по регионам не изменилась, средняя цена возросла бы на 9,8%. Однако, влияние на среднюю цену первого фактора оказалось сильнее, что отражается в следующей взаимосвязи:

Аналогично строятся индексы структурных сдвигов, переменного и фиксированного состава для анализа изменения себестоимости, урожайности и пр.

Заключение

Мы рассмотрели приемы сбора, обработки и анализа статистических данных, которые являются методологическим базисом любой статистической работы. В то же время, необходимо отметить, что статистическое наблюдение не является обязательным этапом статистического исследования. Во многих случаях экономист-аналитик имеет дело с материалом, полученным из баз данных, бюллетеней информационных агентств, статистических сборников и других источников. Тогда работа должна начинаться с проверки полноты и качества данных, их группировки, а при отсутствии необходимости в этих этапах - с расчета индивидуальных и обобщающих показателей.
Рассмотренные приемы и методы с успехом могут использоваться не только в практике статистического анализа. Статистическая методология исследования в настоящее время заняла прочные позиции во многих областях знания. Статистические формулы находят применение в макро- и микроэкономике, оценке бизнеса и недвижимости, финансовом анализе, техническом анализе товарных и финансовых рынков.

Более того, подвергающийся статистической обработке материал не обязательно должен относиться к экономической области. В большинстве случаев, описанные приемы и показатели будут работоспособны и эффективны при обобщении и анализе технической, биологической, медицинской, демографической и социологической информации.
Рассматриваемые в пособии методы в большинстве случаев иллюстрированы практическими примерами. Подобные вычисления при небольших объемах совокупности или коротких динамических рядах не очень трудоемки. При работе же с большими массивами статистической информации необходимо использовать прикладное программное обеспечение, существенно ускоряющее и упрощающее все расчеты. Среди наиболее распространенных современных программных продуктов следует отметить пакеты Мезозавр, ОЛИМП, САНИ, Эвриста, STATISTICA, STATGRAPHICS и SPSS.

Статистика. Курс лекций по теории статистики

12.3.Сводные индексы в средней арифметической и средней гармонической формах

12.4.Системы индексов

12.5.Индексы постоянного и переменного состава

Заключение

Рекомендуемая литература