Статистика. Курс лекций по теории статистики
 Скачать 3.05 Mb. Скачать 3.05 Mb.
|
Глава 12.Индексы12.1.Общие понятия об индексах«Индекс» в переводе с латинского - указатель или показатель. В статистике индексом называют показатель относительного изменения данного уровня исследуемого явления по сравнению с другим его уровнем, принятым за базу сравнения. В качестве такой базы может быть использован или уровень за какой-либо прошлый период времени (динамический индекс), или уровень того же явления по другой территории (территориальный индекс). В статистической практике динамические индексы получили большее распространение. Индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или пространстве две совокупности, элементы которых непосредственно суммировать нельзя. Предположим, нам требуется оценить рост заработной платы работников предприятия в текущем периоде по сравнению с базисным. Такая совокупность является однородной ,и поэтому вполне правомерно суммировать заработную плату работников в каждом периоде, рассчитать средние значения и сравнить их , поделив одну среднюю на другую. Рассмотрим теперь другой случай: нам необходимо оценить рост розничных цен. Здесь уже будет неправомерно складывать цены на разнородные товары, которые могут даже измеряться в различных единицах, а также рассчитывать какие-либо средние показатели. В подобных случаях и применяются индексы. В целом, индексный метод направлен на решение следующих задач: 1) характеристика общего изменения уровня сложного социально-экономического явления; 2) анализ влияния каждого из факторов на изменение индексируемой величины путем элиминирования воздействия прочих факторов; 3) анализ влияния структурных сдвигов на изменение индексируемой величины. В дальнейшем изложении будут использоваться следующие общепринятые обозначения: i - индивидуальный индекс; I - сводный индекс; p - цена; q - количество; z - себестоимость; r - урожайность; s - посевная площадь; 1 - текущий период; 0 - базисный период. Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту: где Например, если цена товара А в текущем периоде составляла 30 руб., а в базисном - 25 руб., то индивидуальный индекс цены будет равен: Индивидуальные индексы, в сущности, представляют собой относительные показатели динамики или темпы роста, и по данным за несколько периодов времени могут рассчитываться в цепной или базисной формах. 12.2.Агрегатные индексыВ тех случаях, когда исследуются не единичные объекты, а состоящие из нескольких элементов совокупности, используются сводные индексы. Исходной формой сводного индекса является агрегатная. При расчете агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все ее элементы. Вернемся к рассмотрению задачи с розничными ценами. Как уже отмечалось, цены различных товаров складывать неправомерно, но суммировать товарооборот по этим товарам вполне допустимо. В текущем периоде такой товарооборот по n товарам составит: Аналогично получим для базисного периода: Если мы сравним товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота: Для иллюстрации этого и последующих индексов воспользуемся следующими условными данными (табл. 11.1.): Таблица 11.1 Цены и объем реализации трех товаров
Рассчитаем индекс товарооборота: Таким образом, товарооборот в целом по данной товарной группе в текущем периоде по сравнению с базисным уменьшился на 2,2% /100% - 97,8%/. Отметим, что размер товарной группы при расчете этого и последующих индексов значения не имеет. На величину полученного индекса товарооборота оказывают влияние как изменение цен на товары, так и изменение объемов их реализации. Для того, чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких показателей как цена и себестоимость физический объем реализации обычно фиксируют на уровне текущего периода. Таким способом получают сводный индекс цен (по методу Пааше): 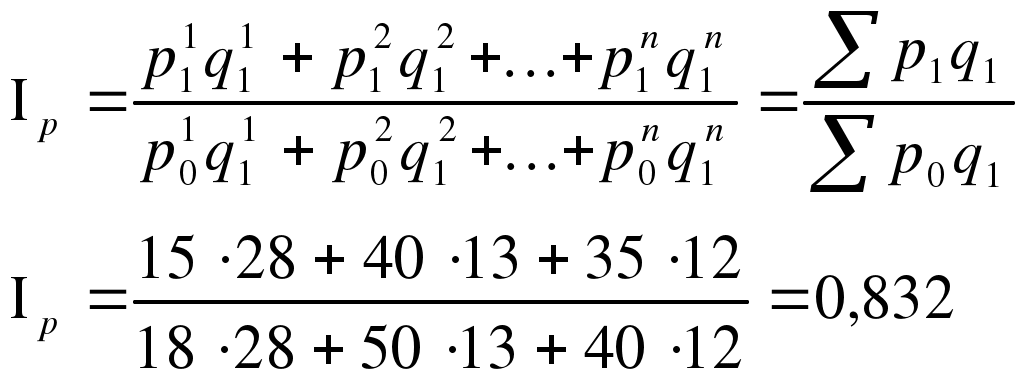 (11.2) (11.2)По данной товарной группе цены в августе по сравнению с июлем снизились на 16,8%. При построении данного индекса цена выступает в качестве индексируемой величины, а количество проданного товара - в качестве веса. Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий отражает имевшее место изменение цен. Числитель и знаменатель сводного индекса цен также можно интерпретировать и по-другому. Числитель представляет собой сумму денег, фактически уплаченных покупателями за товары в текущем периоде. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак «-») или перерасхода («+») покупателей от изменения цен: Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения. Весами в данном случае выступают цены, которые фиксируются на базисном уровне: 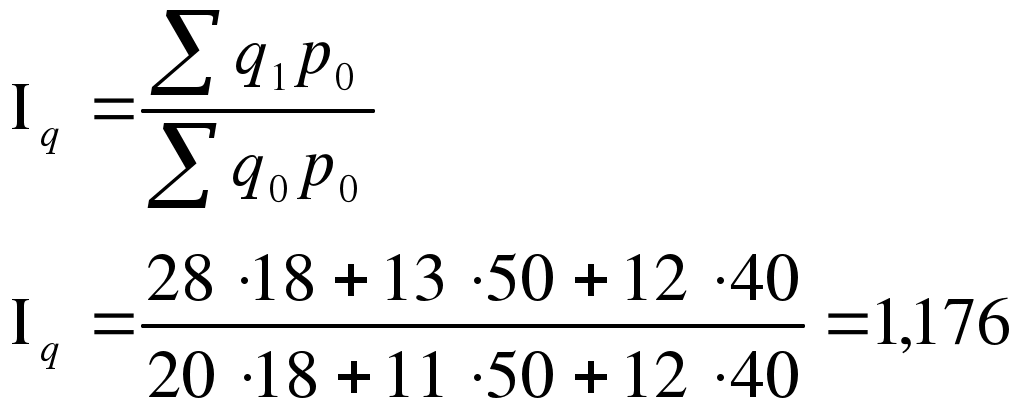 (11.3) (11.3)Физический объем реализации (товарооборота) увеличился на 17,6%. Между рассчитанными индексами существует следующая взаимосвязь: Мы рассмотрели применение индексного метода в анализе товарооборота и цен. Однако, эта же индексная система может использоваться для анализа результатов производственной деятельности предприятий, выпускающих разнородную продукцию. Тогда приведенные выше индексы соответственно называются: Ipq - индекс стоимости продукции; Ip - индекс оптовых цен; Iq - индекс физического объема продукции. Взаимосвязь между этими индексами остается прежней: Еще одна область применения индексов - анализ затрат на производство и себестоимости. Индивидуальный индекс себестоимости характеризует изменение себестоимости отдельного вида продукции в текущем периоде по сравнению с базисным. Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объему производства отдельных видов продукции: Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель - условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии (перерасхода) предприятия от изменения себестоимости: Индекс физического объема продукции, взвешенный по себестоимости, имеет следующий вид: Третьим показателем в данной индексной системе является индекс затрат на производство: Все три индекса взаимосвязаны между собой: Индексный метод также находит применение в статистике сельского хозяйства: индекс валового сбора сельскохозяйственных культур (Irs) может быть получен через индекс урожайности (Ir) и индекс посевных площадей (Is). 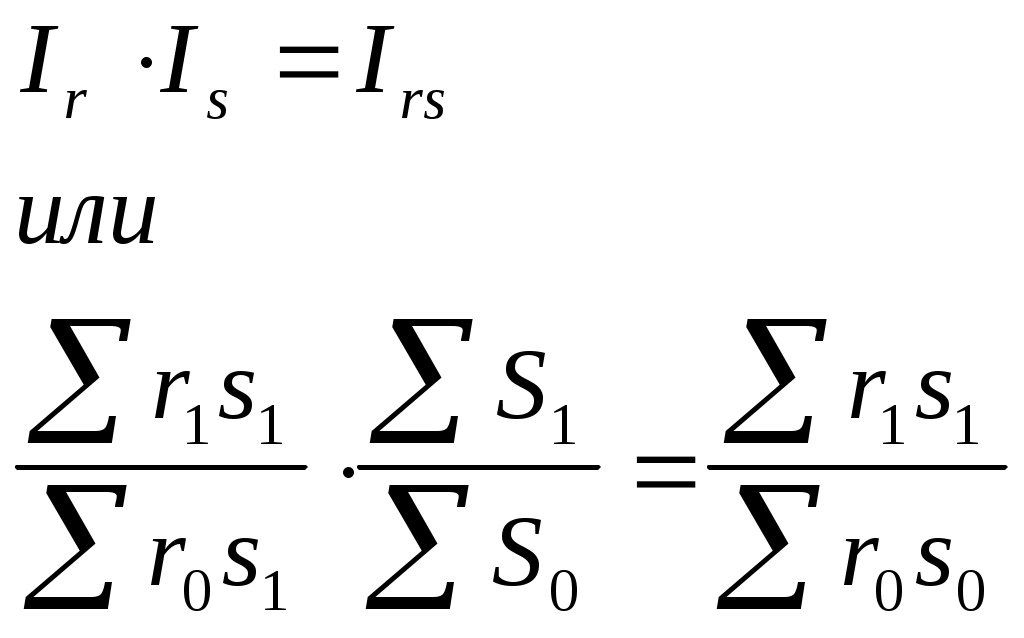 (11.7). (11.7). | |||||||||||||||||||||||||
