Статистика. Курс лекций по теории статистики

• Название: Курс лекций по теории статистики
• Анкор: Статистика
• Дата: 31.01.2022
• Размер: 3.05 Mb.
• Имя файла: Teoria_statistikiLektsii.doc
• Тип: Курс лекций; #347192
• страница: 35 из 37

11.4.Показатели концентрации и централизации

Одна из задач статистического анализа структуры заключается в определении степени концентрации изучаемого признака по единицам совокупности или в оценке неравномерности его распределения. Такая неравномерность может иметь место в распределении доходов по группам населения, жилой площади по группам семей, прибыли по группам предприятий и т.д. При исследовании неравномерности распределения изучаемого признака по территории понятие «концентрация» обычно заменяется понятием «локализация».
Оценка степени концентрации наиболее часто осуществляется по кривой концентрации (Лоренца) и рассчитываемым на ее основе характеристикам. Для этого необходимо иметь частотное распределение единиц исследуемой совокупности и взаимосвязанное с ним частотное распределение изучаемого признака. Для удобства вычислений и повышения аналитичности данных единицы совокупности, как правило, разбиваются на равные группы - 10 групп по 10% единиц в каждой, 5 групп по 20% единиц и так далее.
Наиболее известным показателем концентрации является коэффициент Джини, обычно используемый как мера дифференциации или социального расслоения:

G = 1 - 2 + , (10.11)

где - доля i-ой группы в общем объеме совокупности;

- доля i-ой группы в общем объеме признака;

- накопленная доля i-ой группы в общем объеме признака

Если доли выражены в процентах, данную формулу можно преобразовать:

для 10%-го распределения -

G = 110 - 0,2 (10.12)

для 20%-го распределения -

G = 120 - 0,4 (10.13)

Чем ближе к 1 (100%) значение данного признака, тем выше уровень концентрации; при нуле мы имеем равномерное распределение признака по всем единицам совокупности.
Оценка степени концентрации также может быть получена на основе коэффициента Лоренца:
L = 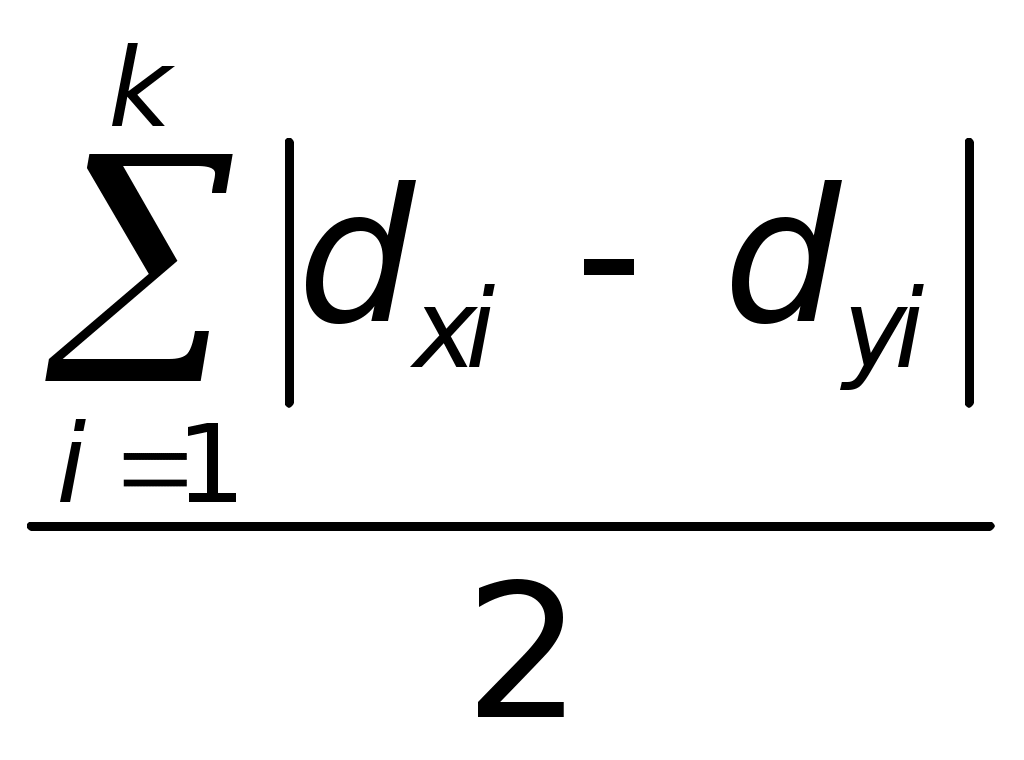(10.14)
При использовании данного коэффициента можно оперировать как долями единицы, так и процентами. Коэффициент Лоренца изменяется в тех же границах, что и коэффициент Джини.
Определим степень концентрации доходов населения по данным таблицы 10.4.:

Таблица 10.4

Распределение доходов населения России в январе - сентябре 1995г.

20%-ные группы населения	Объем денежных доходов
	% к итогу
А	1	2	3	4	5	6	7
Первая (с наименьшими доходами)	5,5	0,055	0,2	0,0110	0,055	0,0110	0,145
Вторая	10,2	0,102	0,2	0,0204	0,157	0,0314	0,098
Третья	15,2	0,152	0,2	0,0304	0,309	0,0618	0,048
Четвертая	22,4	0,224	0,2	0,0448	0,533	0,1066	0,024
Пятая (с наивысшими доходами)	46,7	0,467	0,2	0,0934	1,000	0,2000	0,267
Итого	100,0	1,0	1,0	0,2000	Х	0,4108	0,582

Для расчета коэффициента Джини воспользуемся итоговыми данными граф 4 и 6 таблицы 10.4 :

G = 1 - 2 0,4108 +0,2 = 0,378 или 37,8%.

Такой же результат мы получим, выполнив расчеты в процентах:

G = 120 - 0,4 (5,5 + 15,7 + 30,9 + 53,3 + 100,0) = 37,8%.
Второй способ расчета проще, однако, исходная формула незаменима в тех случаях, когда имеются неравные группы по объему совокупности (в нашем примере - по численности населения).

Используя данные графы 7 таблицы 10.4 определим коэффициент Лоренца:
L = = 0,291 или 29,1%.
Оба коэффициента указывают на относительно высокую степень концентрации доходов населения.
Если под концентрацией понимается степень неравномерности распределения изучаемого признака, не связанная ни с объемом совокупности, ни с численностью отдельных групп, то централизация означает сосредоточение объема признака у отдельных единиц (объема продукции данного вида на отдельных предприятиях, капитала в отдельных банках и т.п.). Обобщающий показатель централизации имеет следующий вид:
, (10.15)
где - значение признака i-ой единицы совокупности;

M - объем признака всей совокупности.

Максимальное значение, равное 1, данный коэффициент достигает лишь в том случае, когда совокупность состоит только из одной единицы, обладающей всем объемом признака. Минимальное значение коэффициента приближается к нулю, но никогда его не достигает.
Рассмотрим следующий пример. Предположим, выпуск продукции А сконцентрирован на 5 предприятиях, расположенных в трех районах области (табл. 10.5.):
Таблица 10.5

Район	Число предприятий	Объем производства, млн.руб.		Доля одного предприятия в
		всего	в среднем на 1 предприятие (гр.2:гр.1)	общем объеме продукции, (гр.3: Итог гр.2)
А	1	2	3	4
А Б В	1 1 3	5374 1225 2610	5374 1225 870	0,584 0,133 0,094
Итого	5	9209	Х	Х

Вычислим показатель централизации производства данного вида продукции:


Рассчитанная величина свидетельствует о высокой степени централизации. Отметим, что аналитическая ценность показателей концентрации и централизации повышается при проведении сравнений во временном или территориальном аспектах.