Статистика. Курс лекций по теории статистики

• Название: Курс лекций по теории статистики
• Анкор: Статистика
• Дата: 31.01.2022
• Размер: 3.05 Mb.
• Имя файла: Teoria_statistikiLektsii.doc
• Тип: Курс лекций; #347192
• страница: 32 из 37

10.5. Методы выявления сезонной компоненты

При рассмотрении квартальных или месячных данных многих социально-экономических явлений часто обнаруживаются определенные, постоянно повторяющиеся колебания, которые существенно не изменяются за длительный период времени. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также ряда многочисленных разнообразных факторов, которые частично являются регулируемыми. В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезонных колебаний» или «сезонных волн», а динамический ряд в этом случае называют тренд-сезонным, или просто сезонным рядом динамики.
Сезонные колебания характеризуются специальным показателями, которые называются индексами сезонности (I_s). Совокупность этих показателей отражает сезонную волну. Индексами сезонности являются процентные отношения фактических внутригодовых уровней к постоянной или переменной средней.
Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам. Данные за несколько лет (обычно не менее трех) берутся для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года.

Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным без их предварительного выравнивания.
Для каждого месяца рассчитывается средняя величина уровня, например, за три года ( ), затем из них рассчитывается среднемесячный уровень для всего ряда ( ) и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, то есть:
(9.22)
Если же ряд динамики содержит определенную тенденцию в развитии, то прежде чем вычислить сезонную волну, фактические данные должны быть обработаны так, чтобы была выявлена общая тенденция. Обычно для этого прибегают к аналитическому выравниванию ряда динамики.
При использовании способа аналитического выравнивания ход вычислений индексов сезонности следующий:

- по соответствующему полиному вычисляются для каждого месяца (квартала) выровненные уровни на момент времени (t);

- вычисляются отношения фактических месячных (квартальных) данных (y_i) к соответствующим выровненным данным ( _t) в процентах

;

- находятся средние арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах I_i=(I₁+I₂+I₃+...+I_n):n, где n - число одноименных периодов.
В общем виде формулу расчета индекса сезонности данным способом можно записать так: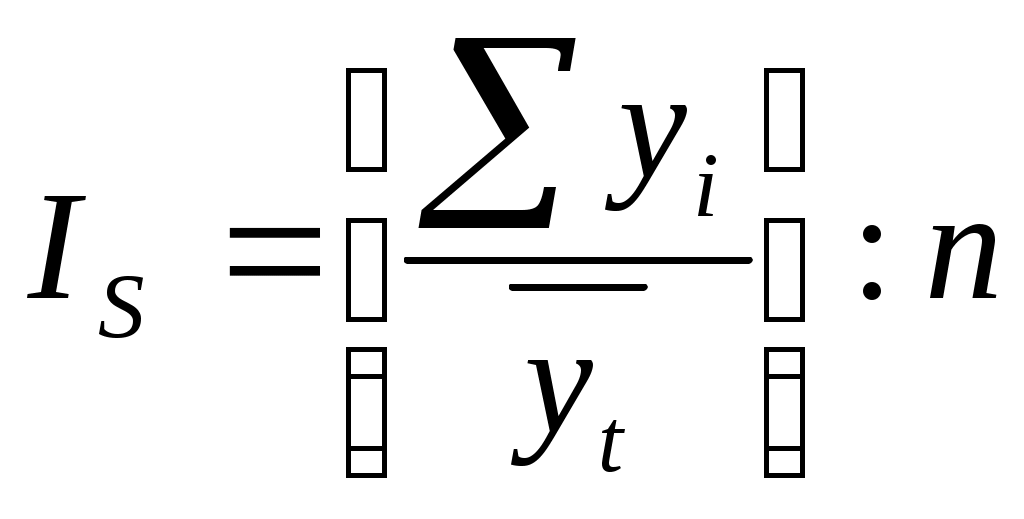
(9.23)
Расчет заканчивается проверкой правильности вычислений индексов, так как средний индекс сезонности для всех месяцев (кварталов) должен быть 100 процентов, то сумма полученных индексов по месячным данным равна 1200, а сумма по четырем кварталам - 400.

10.6. Элементы прогнозирования и интерполяции

Исследования динамики социально-экономических явлений, выявление и характеристика основной тенденции развития дают основание для прогнозирования - определения будущих размеров уровня экономического явления.
Важное место в системе методов прогнозирования занимают статистические методы. Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, то есть прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой и в прошлое - ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевает чаще всего перспективную экстраполяцию.
В зависимости от того, какие принципы и какие исходные данные положены в основу прогноза, можно выделить следующие элементарные методы экстраполяции: среднего абсолютного прироста, среднего темпа роста и экстраполяция на основе выравнивания рядов по какой-либо аналитической формуле.
Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, то есть метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов).
Для нахождения интересующего нас аналитического выражения тенденции на любую дату t необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд, то есть экстраполяцию можно сделать по следующей формуле:
(9.24)
где - экстраполируемой уровень, (i+t) - номер этого уровня (года);

i - номер последнего уровня (года) исследуемого периода, за который рассчитан

t - срок прогноза (период упреждения);

- средний абсолютный прирост.

Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции в этом случае необходимо определить средний коэффициент роста, возведенный в степень, соответствующую периоду экстраполяции, то есть по формуле:
(9.25)
где y_i - последний уровень ряда динамики;

t - срок прогноза;

- средний коэффициент роста.
Если же ряду динамики свойственна иная закономерность, то данные, полученные при экстраполяции на основе среднего темпа роста, будут отличаться от данных, полученных другими способами экстраполяции.
Рассмотренные способы экстраполяции тренда, будучи простейшими, в то же время являются и самыми приближенными.
Поэтому наиболее распространенным методом прогнозирования является аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t).
При таком подходе к прогнозированию предполагается, что размер уровня, характеризирующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени, то есть y=f(t).

Поэтому целесообразно определение доверительных интервалов прогноза.

Величина доверительного интервала определяется следующим образом:
(9.26)
где  - средняя квадратическая ошибка тренда;

- расчетное значение уровня;

t_ - доверительная величина.
Вместо t_ - критерия удобно использовать коэффициент (К^*).

Например, необходимо провести прогноз на 1996-1999 гг. по данным таблицы (9.7) об урожайности зерновых культур в хозяйстве.

Для экстраполяции используем уравнение тренда, полученное по прямой: . Подставив соответствующее значение t в наше уравнение, получим точечные прогнозы на 1996-1999 гг. (графа 2 таблицы 9.8). Для построения интервальных прогнозов рассчитаем среднеквадратическую ошибку тренда (_t=1,797) и используем значения К^*.

Результаты прогноза представлены в таблице (9.8):
Таблица 9.8

Прогнозные значения урожайности зерновых культур в хозяйстве на 1996-1999 гг.

Годы	t		K* 1	tK*
A	1	2	3	4	5
1996	8	16,2	2,0153	3,6	12,6 - 19,8
1997	9	16,3	2,0621	3,7	12,6 - 20,0
1998	10	16,5	2,1131	3,8	12,7 - 20,3
1999	11	16,7	2,1680	3,9	12,8 - 20,6

При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, то есть к интерполяции.

Как и экстраполяция, интерполяция может производится на основе среднего абсолютного прироста, среднего темпа роста, а также с помощью аналитического выравнивания. При интерполяции предполагается, что ни выявленная тенденция, ни ее характер не претерпели существенных изменений в том промежутке времени, уровень (уровни) которого нам неизвестны.