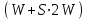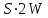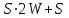фазовые равновесия. Курсовая Фазовые равновесия Выполнила Студентка группы дхм 311 Шамаева Амина Проверила
 Скачать 361.44 Kb. Скачать 361.44 Kb.
|
|
6.2 Задачи Температура кипения ртути под нормальным атмосферным давлением 357  . Теплота парообразования 283,2 Дж/г. Определить изменение упругости пара ртути при изменении температуры на 1 . Теплота парообразования 283,2 Дж/г. Определить изменение упругости пара ртути при изменении температуры на 1 вблизи температуры кипения ртути под нормальным атмосферным давлением. вблизи температуры кипения ртути под нормальным атмосферным давлением.Решение: используем формулу  откуда откуда 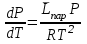 , ,где 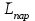 - мольная теплота испарения. Находим - мольная теплота испарения. Находим  ; Т=630К ; Т=630К  . .Давление паров воды при 97  равно 90919,9 равно 90919,9 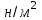 , а при 103 , а при 103 112651,8 112651,8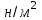 . Определить давление паров воды при 110 . Определить давление паров воды при 110 (Р110). (Р110). Решение: Из формулы 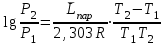 , ,где  - упругости паров, рассчитаем - упругости паров, рассчитаем 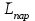 . . 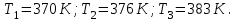 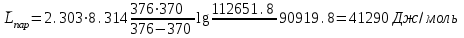 Определим 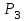 , используя полученное значение , используя полученное значение 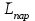 и и  при при 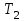 (К). (К). Сравним с табличной величиной  . .3. Удельная теплота плавления нафталина при его нормальной температуре плавления 79,9  равна 149,25 Дж/г. Разность удельных объемов в жидком и твердом состояниях при температуре плавления равна 149,25 Дж/г. Разность удельных объемов в жидком и твердом состояниях при температуре плавления 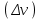 0,146 0,146 . Определить изменение температуры плавления нафталина при увеличении давления в 100 раз по сравнению с нормальным атмосферным давлением (101,325 . Определить изменение температуры плавления нафталина при увеличении давления в 100 раз по сравнению с нормальным атмосферным давлением (101,325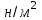 ). ).Решение: Используя уравнение 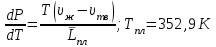 , т.к. давление дано в , т.к. давление дано в 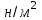 , то изменение удельного объема нужно выразить в , то изменение удельного объема нужно выразить в  , а теплоту плавления в Дж/кг. Поскольку , а теплоту плавления в Дж/кг. Поскольку 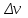 - разность удельных объемов, то вместо мольной теплоты плавления можно взять удельную теплоту плавления (Дж/кг). - разность удельных объемов, то вместо мольной теплоты плавления можно взять удельную теплоту плавления (Дж/кг).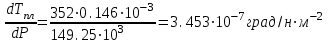 Изменение температуры плавления 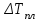 при увеличении давления в 100 раз по сравнению с нормальным атмосферным давлением (т.е. при 1,013 при увеличении давления в 100 раз по сравнению с нормальным атмосферным давлением (т.е. при 1,013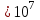 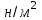 )=3,453 )=3,453 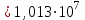 =3,5 =3,5 . .4. Докажите, что на диаграмме “давление – температура” линии равновесия жидкость – пар в однокомпонентной системе всегда должна иметь положительный наклон. Решение: 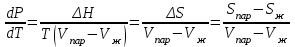 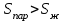 и и 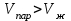 , поэтому , поэтому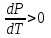 5. Как изменится точка кипения воды (100  ) при изменении атмосферного давления на 1 мм рт.ст.? При 100 ) при изменении атмосферного давления на 1 мм рт.ст.? При 100 и 1 атм. теплота испарения воды 539,7 и 1 атм. теплота испарения воды 539,7 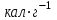 , мольный объем жидкой воды 18,78 мл, мольный объем пара 30,19 литров. , мольный объем жидкой воды 18,78 мл, мольный объем пара 30,19 литров.Решение:  Отсюда  . .6. Плотность твердого фенола 1072 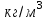 , жидкого 1056 , жидкого 1056 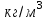 , теплота его плавления 1,044 , теплота его плавления 1,044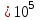 Дж/кг, температура замерзания 314,2 К. Вычислите dP/dT и температуру плавления фенола при 5,065 Дж/кг, температура замерзания 314,2 К. Вычислите dP/dT и температуру плавления фенола при 5,065 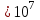 Па. Па.Решение: по уравнению Клапейрона – Клаузиуса рассчитываем dP/dT: 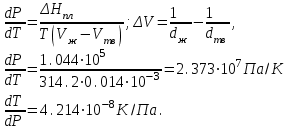 Чтобы вычислить температуру плавления при заданном внешнем давлении, принимаем, что dT/dP в интервале давлений 1,0132 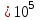 -5,065 -5,065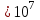 Па – величина постоянная, равная 4,214 Па – величина постоянная, равная 4,214 К/Па. Тогда К/Па. Тогда и и 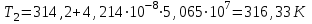 . .7. Для каждой из следующих систем установить число компонентов а) 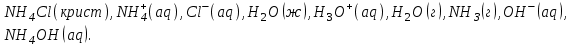 б) 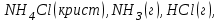 где парциальное давление NH3 не обязательно равно парциальному давлению HCl. где парциальное давление NH3 не обязательно равно парциальному давлению HCl.в) 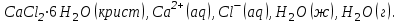 г) 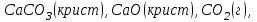 где СаО и СО2 образуется при распаде СаСО3 (крист). где СаО и СО2 образуется при распаде СаСО3 (крист).Решение: а)  б) 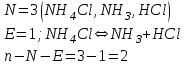 в)  г) 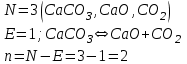 То, что СаО и СО2 присутствуют в стехиометрически равных Количествах, в данном случае не учитывается, т.к. это не влияет на состав фазы. Независимо от соотношения СаО и СО2 состав газообразной фазы всегда 100% СО2 , а состав тв. фазы всегда 100% СаО. 8. Данные по давлению паров чистых хлорбензола и воды даны в таблице.
а) Приняв, что хлорбензол и вода в жидком состоянии полностью не смешиваются друг с другом, определить температуру, при которой хлорбензол будет перегоняться с паром при общем давлении 1 атм. б) Каково будет содержание (вес. %) хлорбензола в дистиллате? Решение: а) Построим график зависимости 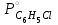 от t (кривая 1) и график зависимости от t (кривая 1) и график зависимости  от t (кривая 2). Исходя из этого графика, для нескольких температур откладываем от t (кривая 2). Исходя из этого графика, для нескольких температур откладываем 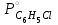 и и  , и строим зависимость ( , и строим зависимость (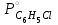 + + ) от t (кривая 3). Кривая 3 описывает зависимость общего давления пара системы С6Н5Сl - H2O от температуры. Температурой кипения системы С6Н5Сl - H2O будет температура, при которой ) от t (кривая 3). Кривая 3 описывает зависимость общего давления пара системы С6Н5Сl - H2O от температуры. Температурой кипения системы С6Н5Сl - H2O будет температура, при которой 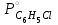 + + =760 мм рт. ст. Как видно из графика (кривая 3), это условие выполняется при t=91,2 =760 мм рт. ст. Как видно из графика (кривая 3), это условие выполняется при t=91,2  . .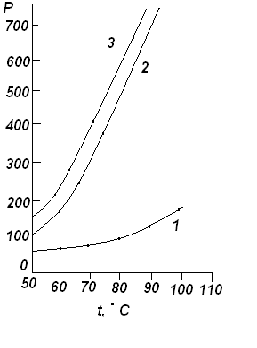 б)  ; А= С6Н5Сl, В= H2O. Температура кипения 92,1 ; А= С6Н5Сl, В= H2O. Температура кипения 92,1 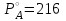 мм рт. ст.; мм рт. ст.; 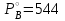 мм рт. ст.; МА=113; МВ=18,0; мм рт. ст.; МА=113; МВ=18,0; 9. Используя приведенные ниже данные, постройте диаграмму для системы хлористый натрий (S) – вода (W). Примите, что твердые растворы не образуются. Обозначьте все области.
Решение: Построим диаграмму 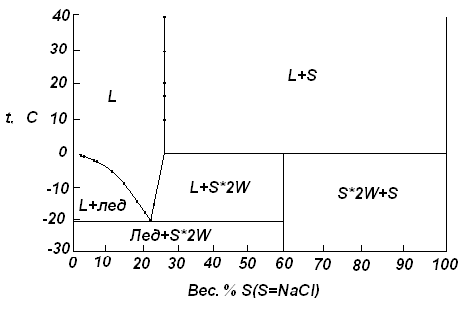 10. Докажите, что для системы, изображенной на рисунке, при равновесии 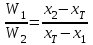 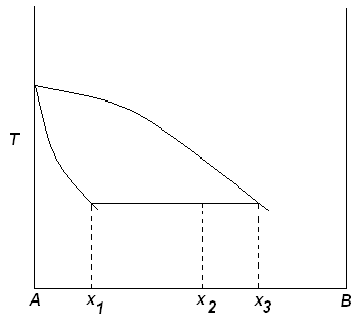 W1 – вес фазы 1, W2 – вес фазы 2, х1 –вес. % В в фазе 1, х2 – вес. % В в фазе 2; хТ – вес. % В во всей системе. Решение: Пусть WТ – общий вес всей системы. Тогда 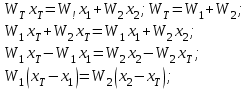 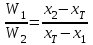 . .Заключение В введении основное внимание уделялось основным определениям фазового равновесия. Далее в работе были рассмотрены правило фаз Гиббса, равновесные состояния при фазовых переходах. К ним относятся: равновесие газ – жидкий раствор в двухкомпонентных системах; равновесие жидкость—жидкость в двухкомпонентных системах; равновесие пар—жидкий раствор в двухкомпонентных системах с ограниченной и неограниченной взаимной растворимостью жидкостей; равновесие пар—жидкий раствор в системах с взаимно нерастворимыми жидкостями. Также было рассмотрено Уравнение Клаузиуса — Клапейрона, в котором Клаузиус показал, как можно упростить уравнение Клапейрона для случаев испарения и возгонки, исходя из предположения, что пар подчиняется закону идеального газа и что мольным объемом жидкости 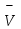 (ж) по сравнению с мольным объемом пара (ж) по сравнению с мольным объемом пара 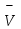 (пар) можно пренебречь. В практической части к данной теме были задано ряд вопросов и 10 задач с решениями. (пар) можно пренебречь. В практической части к данной теме были задано ряд вопросов и 10 задач с решениями.Библиографический список Даниэльс «Физическая химия», Фаррингтон, Олберти; 1978г К. С. Краснов «Физическая химия» том I, Москва «Высшая школа» 2001г Д. Г. Кнорре «Физическая химия», Л. Ф. Крылова, В. С. Музыкантов; Москва «Высшая школа» 1990 г http://ru.wikipedia.org. Лабовиц «Задачи по физической химии с решениями», Аренс; 1972 г Захарченко «Сборник задач и упражнений по физической и коллоидной химии» 1978 г И. И. Климов «Сборник вопроов и задач по физической и коллоидной химии», А. И Филько; 1975 г |