фазовые равновесия. Курсовая Фазовые равновесия Выполнила Студентка группы дхм 311 Шамаева Амина Проверила
 Скачать 361.44 Kb. Скачать 361.44 Kb.
|
|
Федеральное агентство по образованию Астраханский Государственный Университет Кафедра Аналитической и Физической химии Курсовая Фазовые равновесия Выполнила Студентка группы ДХМ 311 Шамаева Амина Проверила к.х.н. доцент Джигола Л.А. Астрахань 2008 год Содержание Введение 2. Правило фаз Гиббса 3. Равновесные состояния при фазовых переходах 3.1 Равновесие газ – жидкий раствор в двухкомпонентных системах 3.1.1 Зависимость растворимости газов в жидкостях от природы газа и растворителя 3.1.2 Зависимость растворимости газов в жидкостях от давления 3.1.3 Зависимость растворимости газов в жидкостях от температуры 3.2 Равновесие жидкость – жидкость в двухкомпонентных системах 3.3 Равновесие пар – жидкий раствор в двухкомпонентных системах 3.3.1 Равновесие пар—жидкий раствор в системах с неограниченной взаимной растворимостью жидкостей 3.3.2 Равновесие пар — жидкий раствор в системах с ограниченной взаимной растворимостью жидкостей 3.3.3 Равновесие пар—жидкий раствор в системах с взаимно нерастворимыми жидкостями 4. Уравнение Клапейрона 5. Уравнение Клаузиуса – Клапейрона 6. Практическая часть 6.1 Вопросы 6.2 Задачи Заключение Библиографический список Введение Гетерогенная система - система, состоящая из нескольких фаз. Фазой называется совокупность гомогенных (однородных) частей системы, одинаковых по составу, химическим и физическим свойствам и отграниченных от других частей системы поверхностью. Поверхности раздела фаз образуются некоторым количеством молекул, расположенных на границе области, заполненной данной фазой. Молекулы, образующие поверхностный слой, находятся в особых условиях, вследствие чего поверхностный слой обладает особыми свойствами, не присущими веществу, находящемуся в глубине фазы. Образования, составленные из небольшого числа молекул, не могут быть разделены на поверхностный слой и внутреннюю массу вещества, поэтому к образованиям с очень малым объемом понятие фаза неприменимо. Жидкие и твердые фазы называются конденсированными. Составляющее вещество системы - это каждое вещество системы, которое может быть выделено из системы и существовать вне ее. Если в системе не протекает химическая реакция, то количество каждого из веществ не зависит от количеств других веществ. Если в системе протекает химическая реакция, то состав фаз равновесной системы можно определить, зная концентрацию только части веществ. Составляющие вещества, концентрации которых определяют состав фаз данной равновесной системы, называют независимыми составляющими веществами или компонентами системы. Свойства системы определяются не только природой компонентов, но и их числом. Число компонентов совпадает с числом составляющих веществ при отсутствии химической реакции или меньше при наличии химической реакции.
2. Правило фаз Гиббса В равновесной системе связь между числами фаз, компонентов и термодинамических степеней свободы выражается правилом фаз Гиббса или законом равновесия фаз. Рассмотрим равновесную термодинамическую систему, состоящую из Ф фаз, каждая из которых содержит К компонентов. Примем в качестве параметров, определяющих состояние системы, давление, температуру и концентрации компонентов, выраженные в массовых или молярных долях или процентах. Оценим общее число параметров состояния и число уравнений, связывающих их. Число параметров, одинаковых во всех фазах системы, равно двум (Р и Т). Поскольку концентрации компонентов выражены в массовых или молярных долях или процентах, то для характеристики состава одной фазы достаточно задать (К — 1) концентраций. Концентрация одного из компонентов данной фазы будет определена, если известны концентрации остальных компонентов. Для характеристики состава всех фаз равновесной системы необходимо знать Ф(К — 1) концентраций. Тогда общее число параметров, определяющих состояние равновесной системы, будет равно Ф(К — 1) + 2. Так как при Р = соnst T=const химические потенциалы компонентов являются функциями их концентраций, например, в идеальном растворе 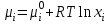 , то число уравнений, связывающих концентрации компонентов равновесной системы, можно определить из равенства химических потенциалов каждого компонента во всех фазах : , то число уравнений, связывающих концентрации компонентов равновесной системы, можно определить из равенства химических потенциалов каждого компонента во всех фазах :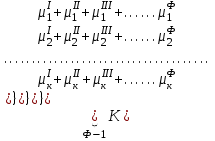 (1) (1)Число уравнений, связывающих концентрации одного компонента, равно (Ф — 1), а всех К компонентов — К(Ф — 1). Число независимых параметров состояния системы, т.е. число термодинамических степеней свободы, равно разности между общим числом параметров, определяющих состояние равновесной системы, и числом уравнений, связывающих эти параметры: С = Ф(К - 1) + 2 - К(Ф - 1), С=К-Ф + 2. (2) Уравнение (2) называется правилом фаз Гиббсаили законом равновесия фаз: в равновесной термодинамической системе, на которую из внешних факторов оказывают влияние только давление и температура. Число термодинамических степеней свободы равно числу компонентов минус число фаз плюс два. Число степеней свободы возрастает с увеличением числа компонентов и уменьшается с увеличением числа фаз. Поскольку число степеней свободы не может быть отрицательным, число фаз в равновесной системе не может превышать К + 2. Правило фаз было выведено американским физиком Дж. Гиббсом в 1876 г. Учение о фазах в дальнейшем было использовано в работах Я. Вант-Гоффа, Б. Розебома, Н.С. Курнакова и др. и явилось основой изучения равновесий в гетерогенных системах. Если из внешних факторов на систему оказывает влияние только давление (Р=соnst) или температура (T=const), число степеней свободы уменьшается на единицу и уравнение правила фаз (2) принимает вид СуСЛ = К-Ф+1 (3) Вариантность системы, рассчитанная по этому уравнению, называется условной (Сусл), а система — условно инвариантной, условно моновариантной и т.д. При постоянстве давления и температуры Cусл=К-Ф (4) Если составы двух равновесных фаз, например жидкой и парообразной, одинаковы, то при подсчете числа степеней свободы следует учитывать еще одно уравнение, связывающее концентрации компонентов Х,(ж) = Х,(п). В этом случае вместо уравнения (2) следует пользоваться уравнением СуСЛ = К-Ф+1 (5) а вместо уравнения (3) — уравнением Cусл=К-Ф (6) Если состояние системы определяется и такими внешними факторами, как электрическое или магнитное поле, поле тяготения и др., то их также следует учитывать при подсчете числа степеней свободы в равновесной системе. В общем случае, когда на систему действуют п различных факторов, то С=К-Ф+n(7) 3. Равновесные состояния при фазовых переходах 3.1 Равновесие газ—жидкий раствор в двухкомпонентных системах При растворении газов в жидкостях устанавливается равновесие между жидкой фазой, содержащей растворитель и растворенный газ, и газовой фазой, содержащей данный газ и пары растворителя. Если растворитель относительно мало летуч, то установится равновесие между раствором и практически чистым растворяемым газом. Растворимость вещества определяется его концентрацией в насыщенном растворе. Растворимость газов в жидкостях зависит от природы растворяемого газа и растворителя, давления газа, температуры и от присутствия в растворе различных веществ, особенно электролитов. Числовое значение растворимости газа в жидкости зависит от способа ее выражения. Растворимость газов выражают числом граммов газа в 100 г чистого растворителя или в 100 г раствора, числом молей газа в 1000 г растворителя или в 1 л раствора, молярной долей. Кроме того, растворимость газов в жидкостях характеризуют коэффициентом растворимости о или коэффициентом поглощения 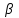 . Коэффициент растворимости равен объему газа, выраженному в кубических метрах, растворенному в 1 м3 растворителя при данной температуре и приведенному к давлению . Коэффициент растворимости равен объему газа, выраженному в кубических метрах, растворенному в 1 м3 растворителя при данной температуре и приведенному к давлению 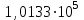 Па (1 атм). Коэффициент поглощения равен объему газа, выраженному в кубических метрах, растворенному в 1 м3 растворителя и приведенному к Р= Па (1 атм). Коэффициент поглощения равен объему газа, выраженному в кубических метрах, растворенному в 1 м3 растворителя и приведенному к Р= 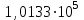 Па (1 атм) и Т= 273 К. Отсюда Па (1 атм) и Т= 273 К. Отсюда 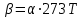 3.1.1 Зависимость растворимости газов в жидкостях от природы газа и растворителя Растворимость различных газов в одном и том же растворителе при одинаковых условиях изменяется в очень широких пределах. Растворимость газов повышается при химическом взаимодействии растворяемого газа с растворителем. На растворимость газов в жидкостях оказывает влияние и природа растворителя. Если растворители относятся к одному и тому же классу соединений, то растворимость газа часто мало зависит от индивидуальных свойств растворителя. В присутствии электролитов растворимость газов в жидкостях уменьшается. Так, при 298 К и 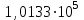 Па в 1 м3 воды растворяется 0,01915 м3 водорода, а в 1 м3 3н NaОН — 0,0072 м3. Влияние электролитов на растворимость газов в водных растворах описывается уравнением И.М.Сеченова: Па в 1 м3 воды растворяется 0,01915 м3 водорода, а в 1 м3 3н NaОН — 0,0072 м3. Влияние электролитов на растворимость газов в водных растворах описывается уравнением И.М.Сеченова: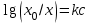 где 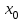 и и 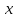 — растворимость газа в воде и в растворе электролита соответственно; k — постоянная, характерная для данного электролита; с — концентрация электролита, моль/л. Уменьшение растворимости газов в присутствии солей называется высаливанием. Высаливающее действие иона повышается с ростом заряда и уменьшается с увеличением радиуса иона. Уменьшение растворимости газов в присутствии электролитов объясняется в основном тем, что ионы притягивают молекулы воды и не притягивают неполярные и слабо поляризуемые молекулы газов, вследствие чего увеличивается фугитивность растворенного газа. — растворимость газа в воде и в растворе электролита соответственно; k — постоянная, характерная для данного электролита; с — концентрация электролита, моль/л. Уменьшение растворимости газов в присутствии солей называется высаливанием. Высаливающее действие иона повышается с ростом заряда и уменьшается с увеличением радиуса иона. Уменьшение растворимости газов в присутствии электролитов объясняется в основном тем, что ионы притягивают молекулы воды и не притягивают неполярные и слабо поляризуемые молекулы газов, вследствие чего увеличивается фугитивность растворенного газа.3.1.2 Зависимость растворимости газов в жидкостях от давления Если газ химически не взаимодействует с растворителем, то зависимость растворимости газа в жидкости от давления выражается законом Генри. Закон Генри справедлив только тогда, когда растворение газа в жидкости не связано с процессами диссоциации или ассоциации молекул растворенного газа. При наличии диссоциации или ассоциации молекул закон Генри следует применять отдельно к каждому роду молекул, концентрации которых не произвольны, а связаны между собой законами химического равновесия и могут быть выражены через общую концентрацию газа в растворе. В этом случае общая концентрация газа уже сложным образом связана с давлением газа над раствором. Однако в ряде случаев пропорциональность сохраняется, и тогда закон Генри остается справедливым. С изменением давления газа растворимость различных газов меняется неодинаково, и подчинение закону Генри наблюдается лишь в области невысоких давлений. Различие в растворимости определяется взаимным влиянием отдельных газов друг на друга в газовой фазе и взаимным влиянием растворенных газов в жидкой фазе. При низких давлениях, когда взаимное влияние отдельных газов невелико, закон Генри справедлив для каждого газа, входящего в газовую смесь, в отдельности. 3.1.3 Зависимость растворимости газов в жидкостях от температуры При небольших давлениях растворимость газов в жидкостях с повышением температуры обычно уменьшается. При высоких давлениях растворимость газов в жидкостях с ростом температуры может и увеличиваться. Так, например, растворимость водорода, гелия, неона и других газов в органических растворителях и водорода в жидком аммиаке увеличивается при повышении температуры. В ряде случаев растворимость газов в жидкостях с ростом температуры проходит через минимум. Количественную зависимость растворимости газов в жидкости от температуры можно найти из условий равновесия между раствором, содержащим растворенный газ, и газовой фазой, которая при малой летучести растворителя представляет собой чистый растворяемый газ. Эта зависимость выражается уравнением: 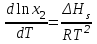 (8) (8) где 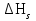 — изменение энтальпии в процессе перехода 1 моль газа из газообразного состояния в состояние насыщенного раствора или последняя теплота растворения. При низких температурах — изменение энтальпии в процессе перехода 1 моль газа из газообразного состояния в состояние насыщенного раствора или последняя теплота растворения. При низких температурах 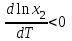 т.е. растворимость газов в жидкостях уменьшается с ростом температуры. В области высоких температур т.е. растворимость газов в жидкостях уменьшается с ростом температуры. В области высоких температур 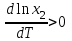 т.е. растворимость газов в жидкостях увеличивается с ростом температуры. При температуре, которой соответствует т.е. растворимость газов в жидкостях увеличивается с ростом температуры. При температуре, которой соответствует 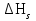 = 0, растворимость газа в жидкости будет минимальной. В небольшом температурном интервалепоследняя теплота растворения = 0, растворимость газа в жидкости будет минимальной. В небольшом температурном интервалепоследняя теплота растворения 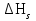 практически постоянна. Тогда в соответствии с уравнением (8) логарифм растворимости газа в жидкости линейно зависит от 1/Т: практически постоянна. Тогда в соответствии с уравнением (8) логарифм растворимости газа в жидкости линейно зависит от 1/Т: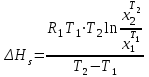 3.2 Равновесие жидкость—жидкость в двухкомпонентных системах Растворы жидкостей в жидкостях очень разнообразны по твоей природе и свойствам. Растворимость жидкостей в жидкостях зависит от природы растворителя и растворенного вещества, температуры, присутствия в растворе посторонних веществ. Существуют растворы с неограниченной взаимной растворимостью, ограниченной взаимной растворимостью и с практически полной взаимной нерастворимостью жидкостей. Ограниченная взаимная растворимость двух жидкостей наблюдается в системах со значительным отклонением от идеальности. Растворимость таких жидкостей зависит от температуры. В одних системах взаимная растворимость жидкостей с ростом температуры увеличивается (системы с верхней критической температурой растворения), в других уменьшается (системы с нижней критической температурой растворения). Под критической температурой растворения понимают ту температуру, при которой составы двух равновесных жидких фаз одинаковы. Для изображения зависимости взаимной растворимости жидкостей от температуры при постоянном давлении строят диаграммы состояния в координатах температура—состав (диаграммы растворимости). При критической температуре растворения оба жидких раствора по составу тождественны, и является условно инвариантной (Сусл = 2 — 2 = 0). К системам с верхней критической температурой растворения относятся системы: вода—анилин, вода—фенол, вода—нитробензол. Иногда взаимная растворимость жидкостей увеличивается как с повышением, так и с понижением температуры (системы с верхней и нижней критическими температурами растворения). В некоторых системах критические температуры растворения не достигаются, так как при повышении температуры одна из жидкостей превращается в пар, а при понижении температуры одна из жидкостей кристаллизуется. 3.3 Равновесие пар—жидкий раствор в двухкомпонентных системах 3.3.1 Равновесие пар—жидкий раствор в системах с неограниченной взаимной растворимостью жидкостей Если раствор образован из двух летучих, неограниченно растворимых друг в друге жидкостей, то пар, находящийся в равновесии с жидким раствором, будет содержать оба компонента. В общем случае состав пара отличается от состава жидкого раствора, из которого он получен. При невысоких давлениях пар можно рассматривать как смесь идеальных газов. Если пар подчиняется законам идеальных газов и находится в равновесии с идеальным раствором, то состав паровой фазы легко найти, зная состав жидкой фазы. Согласно закону Дальтона общее давление пара над идеальным раствором равно сумме парциальных давлений пара компонентов: 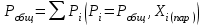 (9) (9)Во всем интервале концентраций идеального жидкого раствора растворитель и растворенное вещество подчиняются закону Рауля: 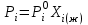 (10) (10)Для бинарного раствора, исходя из (9) и (10), 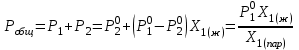 (11) (11)отсюда после некоторых преобразований имеем  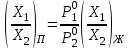 (12) (12)Из уравнения (12) следует, что только при равенстве давлений пара над чистыми компонентами 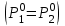 ) состав пара одинаков с составом жидкого раствора, из которого он получен. Во всех остальных случаях, даже для идеальных растворов, состав пара отличается от состава исходного раствора. ) состав пара одинаков с составом жидкого раствора, из которого он получен. Во всех остальных случаях, даже для идеальных растворов, состав пара отличается от состава исходного раствора.Среди реально существующих растворов имеется много таких систем, для которых уравнение (12) позволяет рассчитать состав пара заданном составе жидкого раствора. На практике чаще приходится встречаться с неидеальными растворами, которые не подчиняются закону Рауля. В этих случаях состав пара определяется опытным путем. Для изучения равновесия пар— жидкий раствор применяют два типа диаграмм состояния: диаграммы давление пара — состав (Т — const) диаграммы температура кипения – состав (Р – const) На практике для изучения равновесия пар – жидкий раствор, чаще используются диаграммы температура—состав (диаграммы кипения). Реальные растворы со значительным положительным или отрицательным отклонением от идеальности способны образовывать азеотропные смеси (азеотропы), которые на диаграммах состояния. Азеотропные смеси — это растворы, при испарении которых получается пар того же состава, что и исходная жидкая смесь 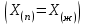 . Азеотропные смеси—условно инвариантные системы (Сусл = 2 — 2 = 0). В реальных растворах азеотропная смесь имеет самую низкую или самую высокую температуру кипения. При изменении внешнего давления изменяется не только температура кипения, но и состав азеотропного раствора. Это указывает на то, что азеотропная смесь не является химическим соединением. Как для идеальных, так и для реальных растворов справедлив первый закон Гиббса—Коновалова: пар по сравнению с жидким раствором, из которого он получен, при равновесии богаче тем компонентом, прибавление которого к раствору приводит к понижению температуры кипения раствора при заданном внешнем давлении или к повышению давления пара над раствором. В системах с азеотропными смесями добавление к раствору более летучего компонента не всегда приводит к повышению давления пара над раствором, т.е. к понижению температуры кипения раствора. Для реальных растворов с азеотропными смесями справедлив также второй закон Гиббса—Коновалова: в азеотропных смесях, составы жидкости и пара совпадают. Азеотропные смеси образуются не только в системах со значительными отклонениями от закона Рауля, но и в системах с незначительными отклонениями, когда компоненты раствора имеют близкие температуры кипения, т.е. почти одинаковые давления пара над чистыми компонентами . Азеотропные смеси—условно инвариантные системы (Сусл = 2 — 2 = 0). В реальных растворах азеотропная смесь имеет самую низкую или самую высокую температуру кипения. При изменении внешнего давления изменяется не только температура кипения, но и состав азеотропного раствора. Это указывает на то, что азеотропная смесь не является химическим соединением. Как для идеальных, так и для реальных растворов справедлив первый закон Гиббса—Коновалова: пар по сравнению с жидким раствором, из которого он получен, при равновесии богаче тем компонентом, прибавление которого к раствору приводит к понижению температуры кипения раствора при заданном внешнем давлении или к повышению давления пара над раствором. В системах с азеотропными смесями добавление к раствору более летучего компонента не всегда приводит к повышению давления пара над раствором, т.е. к понижению температуры кипения раствора. Для реальных растворов с азеотропными смесями справедлив также второй закон Гиббса—Коновалова: в азеотропных смесях, составы жидкости и пара совпадают. Азеотропные смеси образуются не только в системах со значительными отклонениями от закона Рауля, но и в системах с незначительными отклонениями, когда компоненты раствора имеют близкие температуры кипения, т.е. почти одинаковые давления пара над чистыми компонентами 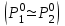 . В этом случае на диаграмме состояния появляется экстремум, лежащий в средней части диаграммы. Чем больше различие между . В этом случае на диаграмме состояния появляется экстремум, лежащий в средней части диаграммы. Чем больше различие между 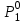 и и 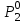 ,тем больше положение экстремума сдвинуто в сторону одного из компонентов системы: при максимуме на кривой давления пара в сторону более летучего компонента, при минимуме — в сторону менее летучего компонента. ,тем больше положение экстремума сдвинуто в сторону одного из компонентов системы: при максимуме на кривой давления пара в сторону более летучего компонента, при минимуме — в сторону менее летучего компонента. |
