|
|
курсовая. распечатать. Вязкость газов Общие понятия и размерность
Введение
Процессы молекулярного переноса в газах (и жидкостях) – вязкость (внутреннее трение), теплопроводность и диффузия – имеют большое значение для правильного объяснения целого ряда физических и физико-химических явлений, а также для решения многих технологических и конструктивных задач, связанных с переносом массы, количества движения и тепла.
Данная курсовая работа посвящена вязкости газов. Исследование вязкости газов и зависимости ее от температуры и давления необходимо прежде всего как изучение одной из основных констант, характеризующих физические свойства веществ.
Насущная необходимость в сведениях по вязкости газов для решения ряда конструктивных и технологических задачах как в промышленной практике, так и в разработке новых технологических процессов и аппаратов, определяется прежде всего тем, что в формулы расчета гидравлического сопротивления и теплообмена коэффициент вязкости входит как один из основных параметров.
Ученые уже давно проводят исследования по данному вопросу. Но не смотря на это вопрос остается актуальным, так как , российская экономика зависит от нефтегазового сектора. А при расчетах трубопроводов, движения газа в пористой среде, сепарации газа и нефти» очистки газа от механических примесей, при определении дебита скважины и др. необходимо знать вязкость газов.
Цель данной работы: углубить теоретические представления о механизмах возникновения, о величине внутреннего трения в газах. Освоить методы измерения вязкости газов.
Глава 1. Вязкость газов
1.1.Общие понятия и размерность
Ньютон впервые высказал в виде гипотезы закон для внутреннего трения.
«Сопротивление, возникшее вследствие недостатка скольжения между частицами жидкости, при прочих равных условиях пропорциональности скорости, с которой частицы отклоняются одна от другой».
На основании этой гипотезы Ньютон сформулировал следующий постулат: « Если твердый, бесконечно длинный цилиндр вращается около оси с постоянной угловой скоростью в бесконечной жидкой среде и если последняя приобретает вращательное движение исключительно за счет импульса, сообщаемого цилиндром, то я утверждаю, что периоды вращения частиц жидкостей пропорциональны их расстояниям от оси цилиндра». Обстоятельная интерпретация и четкая (словесная) формулировка закона внутреннего трения были даны значительно позднее Н. П. Петровым.
Этот закон гласит, что между двумя соседними слоями в направлении, противоположном движению, действует сила ( отнесенная к единице поверхности соприкосновения слоев), пропорциональная изменению скорости в направлении, перпендикулярном движению:
F=η (1). (1).
Более точно в дифференциальной форме эта формула имеет вид
F=η (2). (2).
Коэффициент пропорциональности η называется коэффициентом внутреннего трения или коэффициентом динамической вязкости; в дальнейшем будем называть его просто коэффициентом вязкости.
Из уравнения (1) следует, что величина η равна той силе, которую испытывает единица поверхности одного из слоев со стороны другого слоя, если изменение (градиент) скорости между ними равно единице.
В системе CGS единица вязкости определяется как вязкость вещества, в котором при градиенте скорости 1 см/сек на 1 см на каждый квадратный сантиметр действует сила трения, равная одной дине. Эта единица вязкости называется пуаз и обозначается буквой П, ее сотая часть называется сантипуаз (СП).
Размерность вязкости в физической системе единиц имеет вид
[η]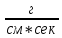 . .
Техническая единица вязкости есть вязкость вещества, в котором при градиенте скорости, равном 1 м/сек на 1м, на каждый квадратный метр действует сила трения в 1 кг.
Отношение коэффициента вязкости к плотности называется коэффициентом кинематической вязкости:
υ=  (3). (3).
В отношении общих свойств приведенных здесь коэффициентов отметим, что они зависят как от рода газа, так и от его состояния (температуры и давления).
 Ниже приводятся соотношения между различными единицами вязкости. Ниже приводятся соотношения между различными единицами вязкости.

1.2.Связь вязкости с другими процессами молекулярного переноса (теплопроводностью и диффузией)
Вязкость газов непосредственно связана с другими процессами молекулярного переноса – диффузией и теплопроводностью. Эти три явления представляют близкую аналогию, все они связаны с переносом какой-либо величины ( вязкость – количества движения, диффузия – массы и теплопроводность – тепловой энергии), причем перенос ее из одной части газа в другую происходит до тех пор, пока данная величина не распределится равномерно по всему объему. Эти процессы необратимы; они ведут к выраниванию плотностей, температур, скоростей, к достижению равновесного состояния, отвечающегося минимуму свободной энергии или максимуму энтропии. С точки зрения кинетической теории механизм всех трех процессов весьма схож, также схожи и уравнения, определяющие их.
Если для вязкости простой молекулярно-кинетический вывод приводит к уравнению η= ρсl (4), ρсl (4),
то для диффузии аналогичный вывод дает: D= сl (5) сl (5)
и для теплопроводности λ= сυ ρсl (6).
Более строгие выводы приводят лишь к замене 1/3 другой численной постоянной.
Соотношения, связывающие коэффициенты D, λ и η имеют вид
D= α , α , α1,3 ,
λ=ɛсυη (7).
Коэффициент ɛ приблизительно равен 2,5 для одноатомных газов, 1,9 для двухатомных и 1,75-4,5 для трех и многоатомных.
Глава 2. Экспериментальные измерения вязкости газов
Экспериментальному измерению вязкости газов и газовых смесей при атмосферном давлении и различных температурах посвящено много работ, проведенных с большой точностью. Меньше измерений было проведено для высоких давлений, однако число таких работ к настоящему времени все же довольно значительно. Измерения вязкости газов при высоких давлениях связаны с большими трудностями и имеющиеся экспериментальные данные менее точны, чем данные, полученные при атмосферном давлении. В области высоких давлений предстоит еще кропотливая исследовательская работа. Поэтому в своей курсовой работе я более подробно разобрала вискозиметры, примененные для высоких давлений.
Наиболее употребительными методами измерения вязкости газов являются: метод капилляра – определение вязкости при протекании газа через трубки малого диаметра, метод падения груза в исследуемом газе и метод затухания вращательных колебаний диска, подвешенного в исследуемом газе. Из этих методов вполне строгое теоретическое обоснование ( подтвержденное экспериментально) имеет метод капилляра.
2.1.Метод капилляра
При явлении вязкости наблюдается перенос импульса от молекул из слоев потока, которые двигаются быстрее, к более медленным. При протекании жидкости или газа в узкой прямолинейной цилиндрической трубе (капилляре) при малых скоростях потока течение является ламинарным, т.е. поток газа движется отдельными слоями, которые не смешиваются между собой. В этом случае слои представляют собой совокупность бесконечно тонких цилиндрических поверхностей, вложенных одна в другую, имеющих общую ось, совпадающую с осью трубы.
Вследствие хаотического теплового движения молекулы непрерывно переходят из слоя в слой и при столкновении с другими молекулами изменяют импульсы своего направленного движения. При переходе из слоя движущегося с большей скоростью в слой, движущийся с меньшей скоростью, молекулы переносят в другой слой свой импульс направленного движения. В «более быстрый» слой переходят молекулы с меньшим импульсом. В результате первый слой тормозится, а второй – ускоряется. Опыт показывает, что импульс dP, который передается от слоя к слою через поверхность площадью S вдоль оси r, перпендикулярной этой поверхности, пропорционален проекции градиента скорости упорядоченного направленного движения на эту ось  , площади S и времени переноса dt: , площади S и времени переноса dt:
dP = –  . (2.1) . (2.1)
В результате между слоями возникает сила внутреннего трения, величина которой по второму закону Ньютона равна:
 , (2.2) , (2.2)
где η – коэффициент вязкости.
Для идеального газа
 υТ , (2.3) υТ , (2.3)
где ρ – плотность газа, λ – средняя длина свободного пробега молекул, υТ – средняя скорость теплового движения молекул, равная
υТ = 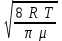 , (2.4) , (2.4)
где μ – молярная масса газа, R – универсальная газовая постоянная.
Рассмотрим газ, движущийся внутри капилляра. Выделим в нем некоторый цилиндрический объем газа радиусом r и длиной l, как показано на рис.1.

Рис.1. Газ, движущийся внутри капилляра.
Обозначим давления на его торцах через P1 и P2. При установившемся течении сила давления на газ в цилиндре
 (2.5) (2.5)
уравновесится силой внутреннего трения FT, которая действует вдоль боковой поверхности цилиндра со стороны окружающего его слоя газа:
 . (2.6) . (2.6)
Так как площадь боковой поверхности S = 2πrl и скорость υ(r) уменьшается при удалении от оси трубы (т.е.  < 0), то из (2.2) получаем: < 0), то из (2.2) получаем:
 . (2.7) . (2.7)
С учетом (2.5) и (2.7) условие стационарности (2.6) запишется в виде:
 . (2.8) . (2.8)
Разделяя переменные, получим следующее уравнение
 , (2.9) , (2.9)
интегрируя которое, получим
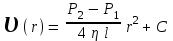 , (2.10) , (2.10)
где С – постоянная интегрирования, определяемая граничными условиями задачи.
При r=R скорость газа должна обратиться в нуль, поскольку сила внутреннего трения о стенку капилляра тормозит смежный с ней слой газа. При этом условии
 (2.11) (2.11)
и
 . (2.12) . (2.12)
Подсчитаем объемный расход газа Vt, т.е. объем газа протекающего за единицу времени через поперечное сечение трубы. Через кольцевую площадку с внутренним радиусом r и внешним r+dr за время t протекает объем газа dV= 2πr dr υ (r) t. Значит, через все сечение трубы за это время пройдет объем
V=  (2.13) (2.13)
и объемный расход Vt=  будет равен будет равен
 Vt= Vt=  . (2.14) . (2.14)
Эту формулу, называемую формулой Пуазейля, можно использовать для экспериментального определения коэффициента вязкости газа.
Формула Пуазейля была получена в предположении ламинарного течения газа или жидкости. Однако с увеличением скорости потока движение становится турбулентным и слои смешиваются. При турбулентном движении скорость в каждой точке меняет свое значение и направление и сохраняется только среднее значение скорости. Критерием характера движения жидкости или газа в трубе служит число Рейнольдса:
 , (2.15) , (2.15)
где  – средняя скорость потока, ρ – плотность жидкости или газа. – средняя скорость потока, ρ – плотность жидкости или газа.
В гладких цилиндрических каналах переход от ламинарного течения к турбулентному происходит при Rе ≈ 1000. Поэтому в случае использования формулы Пуазейля необходимо обеспечить выполнение условия Rе < 1000. Кроме этого, эксперимент необходимо проводить таким образом, чтобы сжимаемостью газа можно было пренебречь. Это возможно тогда, когда перепад давлений вдоль капилляра значительно меньше самого давления. В используемой работе давление газа несколько больше атмосферного (103 см вод. ст.), а перепад давлений составляет 10 см вод. ст., т.е. приблизительно 1 % от атмосферного.
Формула (2.14) справедлива для участка трубы, в котором установилось постоянное течение с квадратичным законом распределения скоростей (2.12) по сечению трубы. Такое течение устанавливается на некотором расстоянии от входа в капилляр, поэтому для достижения достаточной точности эксперимента необходимо выполнение условия R « L ,где R – радиус, L – длина капилляра.
2.2.Метод падения груза в исследуемом газе.
В этом методе газ, перемещающийся вдоль падающего цилиндрического грузика или катящегося шарика, должен пройти через узкий кольцевой зазор между падающим или катящимся грузом и внутренней стенкой трубки.
Сопротивление при падении цилиндрического груза в трубке составляется из трех частей : 1) сопротивления, обусловленного формой струй у концов груза, 2) сопротивления, соответствующего истечению жидкости или газа через кольцевой зазор со скоростью, определяемой площадью поперечного сечения этого зазора и скоростью падения груза, и 3) сопротивления, вызванного вязким торможением от относительного движения двух цилиндрических стенок. При использовании удлиненным падающим цилиндриком в узком кольцевом зазоре первое сопротивление можно сделать относительно очень малым и им пренебречь.
Для вычисления коэффициента вязкости Лавачеком предложена следующая формула:
η=(ρ1-ρ2) (2.16) (2.16)
Так как величину (a – b) с желаемой точностью измерить очень трудно и она обычно неодинакова в различных частях трубки, то прибор калибруется по газу или жидкости, вязкость которых известна. При этом определяется постоянная прибора
c=  (2.17), (2.17),
в которой учитывается также и действие первого сопротивления.
Ниже описывается прибор, основанный на этом методе.
Вискозиметр Штакельбекка.
В перпендикулярно поставленной, точно откалиброванной стеклянной трубе около 12 мм диаметром (рис.2), наполненной исследуемым газом, падает цилиндрический груз под действием силы тяжести. Диаметр падающего груза меньше диаметра стеклянной трубки, так что между ними получается узкая кольцеобразная щель, через которую вытесняемый газ течет вверх.

(Рис.2. Вискозиметр Штакельбекка)
Ясно, что чем большую вязкость имеет газ, тем медленнее падает груз.
Предполагая, что поток в кольцеобразной щели ламинарный, можно определить абсолютную вязкость через измерение времени падения груза внутри некоторого отмеченного интервала. Стеклянная трубка вставляется в стальной цилиндр и снизу герметически закрывается; внутренний диаметр ее изготовляется с точностью до 0,01 мм. Так как верхний конец этой трубки открыт, то давление как внутри трубки, так и в окружающем е пространстве одинаковое. Определение времени падения груза в трубке осуществляется с помощью электрических контактов, соединенных с быстро реагирующим амперметром. В верхней части прикреплен соленоид, который притягивает падающий груз. При прекращении тока в соленоиде груз падает и в конце трубки он соприкасается с контактом. Время падения отсчитывается по секундомеру. Вискозиметр наполняется исследуемым газом через вентиль, расположенный вверху аппарата; давление измеряется пружинным манометром. Стальной цилиндр укреплен подвижно, так что его можно поворачивать на 180 для подведения груза к соленоиду. Для создания необходимой температуры опыта вискозиметр вставляется в термостат.
Следует отметить, что метод падающего цилиндрика в применении его к газам будет достаточно надежным лишь при малых скоростях падения груза, так как только при этом потери на механическое трение центрирующих выступов падающего цилиндрика о стенки трубки, избежать которго полностью невозможно и которое для каждого опыта может быть различным, будут относительно невелики. Для этого зазор между падающим грузом и стенкой должен быть очень малым, что практически трудно выполнимо. Для газов механическое трение падающего груза о стенку трубки будет составлять значительную часть от общего сопротивления, причем точно учесть его невозможно, поэтому здесь метод падающего груза едва ли даст точные результаты, на что и указывает значительное расхождение полученных Штакельбекком значений вязкости, например, для аммиака с данными, полученными методом капилляра.
2.3.Метод затухания вращательных колебаний диска, подвешенного в исследуемом газе
Маятниковые вискозиметры, в которых наблюдается затухание вращательных колебаний диска, были применены многими исследователями для определения вязкости различных газов и газовых смесей. Если диск погрузить в газ или жидкость и заставить совершать крутильные колебания, то эти колебания будут затухающими. Причиной затухания колебаний является вязкость окружающей систему среды.
Амплитуда колебаний монотонно убывает; каждая последующая амплитуда получается из предыдущей умножением последней на один и тот же постоянный множитель; следовательно, последовательные амплитуды колебаний составляют бесконечно убывающую геометрическую прогрессию. Натуральный логарифм отношения величин двух последовательных амплитуд называется логарифмическим декрементом затухания; обозначим эту величину через λ.
Величина логарифмического декремента затухания пропорциональна вязкости, что и является основанием экспериментального метода определения вязкости, предложенного Кулоном. При опыте определяются период колебаний и логарифмический декремент затухания.
Хотя теория этого метода и сейчас еще далека от своего завершения, все же простота конструкции вискозиметра и особенно удобство применения этого метода при низких и высоких температурах обусловили его широкое применение.
Формула для вычисления вязкости, впервые предложенная Максвеллом, имеет следующий вид:
η= (2.18) (2.18)
Большинство исследователей при вычислении коэффициентов вязкости пользовались этой формулой.
Заключение
Изучение вопросов, рассмотренных в данной работе, имело практическое значение в таких областях, как гидросооружения, гидрогеология, машиностроение, экономика и т.д. Благодаря открытым свойствам жидкостей и газов были сооружены летательные аппараты, экономически выгодные транспортировки нефти и газа, изучены свойства подземных вод и зон турбулентности.
Динамика этих двух агрегатных состояний, а точнее теоретическое обоснование особенностей перемещения жидких и газообразных тел позволило человечеству усовершенствовать свои изобретения, а также подарило человеку крылья.
Список используемой литературы
1) Д.А.Фридрихсберг Курс Коллоидной химии.для высшей школы; Санкт-Петербург «химия» 1995
2) Б.М.Яворский и А.А.Детлаф Справочник по Физике (для инженеров и сотрудников вузов); Издательство «НАУКА»; Москва 1965 г.
3) И.В.Савельев Курс общей физики, книга 3 молекулярная физика и термодинамика; Москва «НАУКА» 2005 г.
4) А.К.Кикоин, И.К.Кикоин Молекулярная физика; Издательство «НАУКА» Главная редакция Физико-Математической литературы Москва 1976 г.
5) Н.Б Урьев Физико-химические основы технологии дисперсных систем и материалов, Москва 2003г.
|
|
|
 Скачать 0.92 Mb.
Скачать 0.92 Mb.