ОФС_Статистическая_обработка_результатов_физических__физико-хими. Статья статистическая обработка результатов физических, физикохимических и химических испытаний
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
ОБЩАЯ ФАРМАКОПЕЙНАЯ СТАТЬЯ Статистическая обработка результатов физических, физико-химических и химических испытаний Настоящая общая фармакопейная статья содержит сведения об основных статистических подходах к обработке и оценке данных, полученных при проведении испытаний лекарственных средств физическими, физико-химическими и химическими методами анализа. Задача статистической обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится истинное значение. Статистические методы обработки результатов измерений используют для описания полученных данных, наиболее близких к истинному значению, для оценки систематических и случайных погрешностей измерений ‒ результатов испытаний. Статистическая обработка результатов физических, физико-химических и химических испытаний, которые могут быть изменчивыми, позволяет научно обосновывать и корректно интерпретировать полученные аналитические данные, а затем на их основе решать ряд прикладных задач, связанных с определением статистической достоверности результатов испытаний лекарственных средств. Правильное применение статистических принципов к аналитическим данным испытаний лекарственных средств возможно при условии, что такие данные собраны, зарегистрированы прослеживаемым образом и не содержат систематических ошибок. Получение таких данных необходимо осуществлять в соответствии с требованиями ОФС «Отбор проб», «Стандартные образцы», «Валидация аналитических методик». Представленные в настоящей общей фармакопейной статье данные носят информационный характер и не являются исчерпывающими. Условные обозначения А – измеряемая величина; a – свободный член линейной зависимости; b– угловой коэффициент линейной зависимости; F– критерий Фишера; f – число степеней свободы; функция плотности вероятности нормального распределения; i – порядковый номер варианты; L – фактор, используемый при оценке сходимости результатов параллельных определений; т, п – объемы выборки; P – доверительная вероятность без конкретизации постановки задачи; (P2), (P1) – доверительная вероятность соответственно при двух- и односторонней постановке задачи; Q1, Qn– контрольные критерии для идентификации грубых погрешностей; R– размах варьирования; Rc– общий индекс корреляции (линейной); r– (линейный) коэффициент корреляции; RSD = sr·100% – относительное стандартное отклонение, %; RSD  = s = s r·100% – относительное стандартное отклонение среднего значения, %; r·100% – относительное стандартное отклонение среднего значения, %;s– стандартное отклонение; sr– относительное (по отношению к среднему результату) стандартное отклонение; s2– дисперсия; s2r– относительная дисперсия; σ2 – дисперсия генеральной совокупности; s 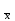 – стандартное отклонение среднего результата; – стандартное отклонение среднего результата;s  r – относительное (по отношению к среднему результату) стандартное отклонение среднего результата; r – относительное (по отношению к среднему результату) стандартное отклонение среднего результата;slg – логарифмическое стандартное отклонение; s2lg – логарифмическая дисперсия; slg 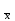 – логарифмическое стандартное отклонение среднего результата; – логарифмическое стандартное отклонение среднего результата;s 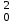 , s , s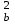 , s , s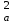 – общая дисперсия и дисперсия коэффициентов линейной – общая дисперсия и дисперсия коэффициентов линейнойзависимости; t – критерий Стьюдента; U– коэффициент для расчета границ среднего результата гарантии качества испытуемого продукта; х, у – текущие координаты в уравнении линейной зависимости; Хi, Yi – вычисленные, исходя из уравнения линейной зависимости, значения переменных х и у;  , , 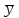 – средние значения выборки (координаты центра линейной зависимости); – средние значения выборки (координаты центра линейной зависимости);хi,, yi – i-тая варианта (i-тая пара экспериментальных значений х и у);  ± ∆ ± ∆ – граничные значения доверительного интервала среднего – граничные значения доверительного интервала среднегорезультата; хi ± ∆х– граничные значения доверительного интервала результата единичного определения; dили ∆ – разность некоторых величин; p – уровень значимости, степень надежности; ∆х – полуширина доверительного интервала неопределенности единичного определения; ∆  – полуширина доверительного интервала неопределенности среднего результата; – полуширина доверительного интервала неопределенности среднего результата;∆х,r– полуширина относительного доверительного интервала неопределенности единичного определения; ∆  ,r– полуширина относительного доверительного интервала неопределенности среднего результата; ,r– полуширина относительного доверительного интервала неопределенности среднего результата;ΔAS:r– суммарная неопределенность анализа; ΔFAO,r– неопределенность конечной аналитической операции; ΔRS,r– неопределенность аттестации стандартного образца; ΔSP,r– неопределенность пробоподготовки; δ – относительная величина систематической погрешности; ε, 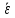 – относительные неопределенности, соответственно, результата отдельного определения и среднего результата; – относительные неопределенности, соответственно, результата отдельного определения и среднего результата;µ – истинное значение измеряемой величины; ∑ – знак суммирования (сумма); X2 – критерий хи-квадрат. В настоящей общей фармакопейной статье используются некоторые термины, определение которых приведено в ОФС «Валидация аналитических методик» и ОФС«Отбор проб». 1.Выборка и основные статистические характеристики однородной выборки 1.1.Выборка При статистической обработке результатов физических, физико-химических и химических испытаний используют термин «выборка» для обозначения совокупности реально полученных, статистически эквивалентных результатов испытаний (вариант). В качестве такой совокупности можно, например, рассматривать ряд результатов, полученных при параллельных определениях содержания какого-либо вещества (величины x) в однородной по составу пробе. Количество полученных результатов представляет собой число наблюдений n, образующих выборку, называемых «объемом выборки» Отдельные значения вариант выборки объема п обозначают через xi (1≤ i ≤n). Упорядоченная в порядке возрастания вариант выборка может быть представлена в виде: x1; х2; ... хi; ...хn-1; хn. (1.1) При статистической обработке результатов физических, физико-химических и химических испытаний различают выборку малого (n ≤ 10) и большого объема (n 10). В других случаях статистической обработки результатов выборка «малого объема» может быть определена, как не превышающая 30 (n ≤ 30). 1.2.Среднее значение, дисперсия, стандартное отклонение В большинстве случаев среднее значение выборки 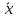 является наилучшей оценкой истинного значения измеряемой величины µ, если его вычисляют как среднее арифметическое всех вариант: является наилучшей оценкой истинного значения измеряемой величины µ, если его вычисляют как среднее арифметическое всех вариант: = = 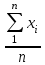 . (1.2) . (1.2)При этом разброс вариант хiвокруг среднего значения 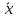 характеризуется величиной стандартного отклонения s. При количественном определении веществ методами физического, физико-химического и химического анализа величину s часто рассматривают как меру случайной погрешности, свойственной данной методике анализа. Квадрат этой величины s2 называют дисперсией. Величина дисперсии может рассматриваться как мера прецизионности (сходимости) результатов, представленных в данной выборке. Вычисление величин s и s2 проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений di и число степеней свободы (число независимых вариант) f: характеризуется величиной стандартного отклонения s. При количественном определении веществ методами физического, физико-химического и химического анализа величину s часто рассматривают как меру случайной погрешности, свойственной данной методике анализа. Квадрат этой величины s2 называют дисперсией. Величина дисперсии может рассматриваться как мера прецизионности (сходимости) результатов, представленных в данной выборке. Вычисление величин s и s2 проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений di и число степеней свободы (число независимых вариант) f:di= xi–  , (1.3) , (1.3)f = n – 1, (1.4) s2 = 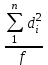 = = 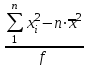 , (1.5) , (1.5)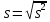 (1.6) (1.6)Стандартное отклонение среднего результата 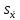 рассчитывают по уравнению: рассчитывают по уравнению: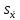 = = 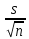 (1.7) (1.7)При обработке результатов испытаний лекарственных средств во многих случаях целесообразно использовать относительные (по отношению к 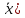 величины, например, относительное стандартное отклонение sr, относительную дисперсию величины, например, относительное стандартное отклонение sr, относительную дисперсию 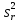 и относительное стандартное отклонение среднего результата и относительное стандартное отклонение среднего результата 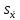 ,r. Их рассчитывают по формулам: ,r. Их рассчитывают по формулам: 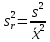 (1.5а) (1.5а)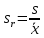 (1.6а) (1.6а)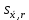 = = 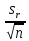 (1.7а) (1.7а)Указанные относительные величины в зависимости от решаемой задачи могут выражаться в процентах относительно 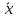 . В этом случае их часто обозначают RSD и . В этом случае их часто обозначают RSD и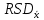 , соответственно: , соответственно:RSD = sr ·  100 % (1.6б) 100 % (1.6б)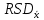 = = 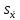 ,r · 100 % (1.7б) ,r · 100 % (1.7б)Относительное стандартное отклонение среднего результата, выраженное в процентах 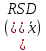 называют коэффициентом вариации. При обработке результатов испытаний лекарственных средств абсолютные величины обычно используют для прямых, а относительные ‒ для косвенных методов анализа. называют коэффициентом вариации. При обработке результатов испытаний лекарственных средств абсолютные величины обычно используют для прямых, а относительные ‒ для косвенных методов анализа.Если при измерениях получают логарифмы искомых вариант, среднее значение выборки вычисляют как среднее геометрическое, используя логарифм вариант:  g = g = 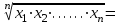 antilg (lg antilg (lg g).(1.8), g).(1.8),далее: lg  g = g = 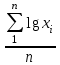 , (1.9) , (1.9)Значения s2, s и s 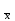 в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через s в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через s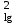 , slg, slg , slg, slg g.. g.. Пример вычисления среднего значения и дисперсии приведен в разделе 6.1. 1.3.Проверка однородности выборки. Исключение выпадающих значений вариант Результаты, полученные при статистической обработке выборки, будут достоверными лишь в том случае, если эта выборка однородна, т.е. если варианты, составляющие выборку, не отягощены грубыми погрешностями, допущенными при измерении или расчете. Для принятия решения об исключении таких выпадающих значений вариант, перед окончательным вычислением статистических характеристик проводят проверку однородности выборки, используя различные подходы в зависимости от объема выборки. Вместе с тем, следует учитывать, что могут быть такие испытания лекарственных препаратов, которые предусматривают проверку данных каждой из вариант выборки без предварительной оценки ее однородности и исключения вариант, например, при определении показателя «Однородность дозированных единиц» в соответствии с ОФС «Однородность дозированных единиц», когда должны быть учтены и проанализированы все полученные результаты (значения вариант). Для проверки однородности выборки и исключения резко выделяющихся, выпадающих, отягощенных грубыми погрешностями, значений вариант используют различные подходы в зависимости от объема выборки. Для проверки однородности выборок малого и большого объема наиболее часто используют следующие подходы. Подход 1. Проверку однородности выборок малого объема (n ≤ 10) осуществляют без предварительного вычисления статистических характеристик. С этой целью все значения выборки представляют в виде (1.1) и предполагают, что крайние, граничные значения вариант выборки, то есть, x1 и xn, являются выпадающими, отягощенными грубыми погрешностями. Для этих крайних значений выборки рассчитывают значения контрольного критерия для идентификации грубых погрешностей Q, исходя из величины размаха варьирования (размаха вариации) R, то есть разности значений между x1 и xn. R = 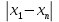 для n = 3-7 (1.10a) для n = 3-7 (1.10a)R = 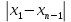 для n= 8-10 (1.10б) для n= 8-10 (1.10б)Q1 = 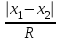 , (1.11а) , (1.11а)Qn= 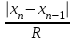 . (1.11б) . (1.11б)Выборка признается неоднородной, если хотя бы одно из вычисленных значений Q превышает критическое значение контрольного критерия Q (Р,n), найденное для доверительной вероятности Р (Таблица7.1) . Варианты х1 или xn, которым соответствует значение Q > Q(Р,n), отбрасывают и для полученной выборки уменьшенного объема выполняют новый цикл вычислений по уравнениям (1.10) и (1.11) с целью проверки ее однородности. Если в исходной выборке следующие значения вариант: 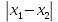 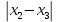 и и 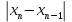 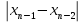 , то уравнения (1.11а) и (1.11б) принимают вид: , то уравнения (1.11а) и (1.11б) принимают вид: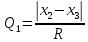 (1.12а) (1.12а)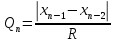 (1.12б) (1.12б) Полученная в конечном счете однородная выборка используется для вычисления 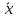 , s2, s и s , s2, s и s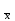 . .Пример проверки однородности выборки малого объема приведен в разделе 6.2. Подход 2. Для проверки однородности выборки большого объема (n > 10) целесообразно проводить предварительную статистическую обработку всей выборки, полагая ее однородной, и уже затем на основании найденных статистических характеристик решать вопрос о справедливости сделанного предположения об однородности согласно уравнению (1.13). Вычисляют статистические характеристики  , s2, s, s , s2, s, s для выборки большого объема и проверяют ее однородность. Выборка признается однородной, если для всех вариант выполняется условие: для выборки большого объема и проверяют ее однородность. Выборка признается однородной, если для всех вариант выполняется условие: ≤ 3·s. (1.13) ≤ 3·s. (1.13)Если выборка признана неоднородной, то варианты, для которых |di| > 3·s, отбрасывают как отягощенные грубыми погрешностями с доверительной вероятностью Р > 99,0 %. В этом случае для полученной выборки сокращенного объема повторяют цикл вычислений статистических характеристик по уравнениям (1.2) - (1.7) и снова проводят проверку однородности. Вычисление статистических характеристик считают законченным, когда выборка сокращенного объема оказывается однородной. |
