Таблица 7.5. - Процентные точки распределения 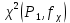
f
|
P1=95%
|
P1=99%
|
1
|
3,841
|
6,635
|
2
|
5,991
|
9,210
|
3
|
7,815
|
11,345
|
4
|
9,488
|
13,277
|
5
|
11,070
|
15,086
|
6
|
12,592
|
16,812
|
7
|
14,067
|
18,475
|
8
|
15, 507
|
20,090
|
9
|
16,919
|
21,666
|
10
|
18,307
|
23,209
|
11
|
19,675
|
24,725
|
12
|
21,026
|
26,217
|
13
|
22,362
|
27,688
|
14
|
23,685
|
29,141
|
15
|
24,996
|
30,578
|
16
|
26,296
|
32,000
|
17
|
27,587
|
33,409
|
18
|
28,869
|
34,805
|
19
|
30,144
|
36,191
|
20
|
31,410
|
37,566
|
21
|
32,671
|
38,932
|
22
|
33,924
|
40,289
|
23
|
35,172
|
41,638
|
24
|
36,415
|
42,980
|
25
|
37,652
|
44,314
|
26
|
38,885
|
45,642
|
27
|
40,113
|
46,963
|
28
|
41,337
|
48,278
|
29
|
42,557
|
49,588
|
30
|
43,773
|
50,892
|
40
|
55,758
|
63,691
|
50
|
67,505
|
76,154
|
P1- вероятность того, что оцениваемое значение 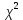 не превышает табличное. Это оцениваемое значение рассматривается как значимое (P1=95%) или как высоко значимое (P1=99%). не превышает табличное. Это оцениваемое значение рассматривается как значимое (P1=95%) или как высоко значимое (P1=99%).
|
Таблица 7.6. Критерий Кохрена.
Критические точки статистики G = 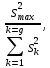 построенной по gнезависимым оценкам дисперсии ( построенной по gнезависимым оценкам дисперсии (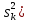 , каждая из которых обладает fстепенями свободы. , каждая из которых обладает fстепенями свободы.
f→
g↓
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
16
|
36
|
∞
|
G(Р=95%)
|
2
|
0,9985
|
0,9750
|
0,9392
|
0,9057
|
0,8772
|
0,8534
|
0,8332
|
0,8159
|
0,8010
|
0,7880
|
0,7341
|
0,6602
|
0,5000
|
3
|
0,9669
|
0,8709
|
0,7977
|
0,7457
|
0,7071
|
0,6771
|
0,6530
|
0,6333
|
0,6167
|
0,6025
|
0,5466
|
0,4748
|
0,3333
|
4
|
0,9065
|
0,7679
|
0,6841
|
0,6287
|
0,5895
|
0,5598
|
0,5365
|
0,5175
|
0,5017
|
0,4884
|
0,4366
|
0,3720
|
0,2500
|
5
|
0,8412
|
0,6838
|
0,5981
|
0,5440
|
0,5063
|
0,4783
|
0,4564
|
0,4387
|
0,4241
|
0,4118
|
0,3645
|
0,3066
|
0,2000
|
6
|
0,7808
|
0,6161
|
0,5321
|
0,4803
|
0,4447
|
0,4184
|
0,3980
|
0,3817
|
0,3682
|
0,3568
|
0,3135
|
0,2612
|
0,1667
|
7
|
0,7271
|
0,5612
|
0,4800
|
0,4307
|
0,3974
|
0,3726
|
0,3535
|
0,3384
|
0,3259
|
0,3154
|
0,2756
|
0,2278
|
0,1429
|
8
|
0,6798
|
0,5157
|
0,4377
|
0,3910
|
0,3595
|
0,3362
|
0,3185
|
0,3043
|
0,2926
|
0,2829
|
0,2462
|
0,2022
|
0,1250
|
9
|
0,6385
|
0,4775
|
0,4027
|
0,3584
|
0,3286
|
0,3067
|
0,2901
|
0,2768
|
0,2659
|
0,2568
|
0,2226
|
0,1820
|
0,1111
|
10
|
0,6020
|
0,4450
|
0,3733
|
0,3311
|
0,3029
|
0,2823
|
0,2666
|
0,2541
|
0,2439
|
0,2353
|
0,2032
|
0,1655
|
0,1000
|
12
|
0,5410
|
0,3924
|
0,3264
|
0,2880
|
0,2624
|
0,2439
|
0,2299
|
0,2187
|
0,2098
|
0,2020
|
0,1737
|
0,1403
|
0,0833
|
15
|
0,4709
|
0,3346
|
0,2758
|
0,2419
|
0,2195
|
0,2034
|
0,1911
|
0,1815
|
0,1736
|
0,1671
|
0,1429
|
0,1144
|
0,0667
|
20
|
0,3894
|
0,2705
|
0,2205
|
0,1921
|
0,1735
|
0,1602
|
0,1501
|
0,1422
|
0,1357
|
0,1303
|
0,1108
|
0,0879
|
0,0500
|
24
|
0,3434
|
0,2354
|
0,1907
|
0,1656
|
0,1493
|
0,1374
|
0,1286
|
0,1216
|
0,1160
|
0,1113
|
0,0912
|
0,0743
|
0,0417
|
30
|
0,2929
|
0,1980
|
0,1593
|
0,1377
|
0,1237
|
0,1137
|
0,1061
|
0,1002
|
0,0958
|
0,0921
|
0,0771
|
0,0604
|
0,0333
|
40
|
0,2370
|
0,1576
|
0,1259
|
0,1082
|
0,0968
|
0,0887
|
0,0827
|
0,0780
|
0,0745
|
0,0713
|
0,0595
|
0,0462
|
0,0250
|
60
|
0,1737
|
0,1131
|
0,0895
|
0,0765
|
0,0682
|
0,0623
|
0,0583
|
0,0552
|
0,0520
|
0,0497
|
0,0411
|
0,0316
|
0,0167
|
∞
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
f→
g↓
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
16
|
36
|
∞
|
G(Р=99%)
|
2
|
0,9999
|
0,9950
|
0,9794
|
0,9586
|
0,9373
|
0,9172
|
0,8988
|
0,8823
|
0,8674
|
0,8539
|
0,7949
|
0,7067
|
0,5000
|
3
|
0,9933
|
0,9423
|
0,8831
|
0,8335
|
0,7933
|
0,7606
|
0,7335
|
0,7107
|
0,6912
|
0,6743
|
0,6059
|
0,5153
|
0,3333
|
4
|
0,9676
|
0,8643
|
0,7814
|
0,7212
|
0,6761
|
0,6410
|
0,6129
|
0,5897
|
0,5702
|
0,5536
|
0,4884
|
0,4057
|
0,2500
|
5
|
0,9279
|
0,7885
|
0,6957
|
0,6329
|
0,5875
|
0,5531
|
0,5259
|
0,5037
|
0,4854
|
0,4697
|
0,4094
|
0,3351
|
0,2000
|
6
|
0,8828
|
0,7218
|
0,6258
|
0,5635
|
0,5195
|
0,4866
|
0,4608
|
0,4401
|
0,4229
|
0,4081
|
0,3529
|
0,2858
|
0,1667
|
7
|
0,8376
|
0,6644
|
0,5685
|
0,5080
|
0,4659
|
0,4347
|
0,4105
|
0,3911
|
0,3751
|
0,3616
|
0,3105
|
0,2494
|
0,1429
|
8
|
0,7945
|
0,6152
|
0,5209
|
0,4627
|
0,4226
|
0,3932
|
0,3704
|
0,3522
|
0,3373
|
0,3248
|
0,2779
|
0,2214
|
0,1250
|
9
|
0,7544
|
0,5727
|
0,4810
|
0,4251
|
0,3870
|
0,3592
|
0,3378
|
0,3207
|
0,3067
|
0,2950
|
0,2514
|
0,1992
|
0,1111
|
10
|
0,7175
|
0,5358
|
0,4469
|
0,3934
|
0,3572
|
0,3308
|
0,3106
|
0,2945
|
0,2813
|
0,2704
|
0,2297
|
0,1811
|
0,1000
|
12
|
0,6528
|
0,4751
|
0,3919
|
0,3428
|
0,3099
|
0,2861
|
0,2680
|
0,2535
|
0,2419
|
0,2320
|
0,1961
|
0,1535
|
0,0833
|
15
|
0,5747
|
0,4069
|
0,3317
|
0,2882
|
0,2593
|
0,2386
|
0,2228
|
0,2104
|
0,2002
|
0,1918
|
0,1612
|
0,1251
|
0,0667
|
20
|
0,4799
|
0,3297
|
0,2654
|
0,2288
|
0,2048
|
0,1877
|
0,1748
|
0,1646
|
0,1567
|
0,1501
|
0,1248
|
0,0960
|
0,0500
|
24
|
0,4247
|
0,2871
|
0,2295
|
0,1970
|
0,1759
|
0,1608
|
0,1495
|
0,1406
|
0,1338
|
0,1283
|
0,1060
|
0,0810
|
0,0417
|
30
|
0,3632
|
0,2412
|
0,1913
|
0,1635
|
0,1454
|
0,1327
|
0,1232
|
0,1157
|
0,1100
|
0,1054
|
0,0867
|
0,0658
|
0,0333
|
40
|
0,2940
|
0,1915
|
0,1508
|
0,1281
|
0,1135
|
0,1033
|
0,0957
|
0,0898
|
0,0853
|
0,0816
|
0,0668
|
0,0503
|
0,0250
|
60
|
0,2151
|
0,1371
|
0,1069
|
0,0902
|
0,0796
|
0,0721
|
0,0668
|
0,0625
|
0,0594
|
0,0567
|
0,0461
|
0,0344
|
0,0167
|
∞
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
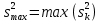 .; .;
P ̶ вероятность того, что все gоценок дисперсии являются выборочными значениями одной и той же генеральной совокупности. Гипотеза равенства дисперсий может быть значимой (P =95 %) или высоко значимой (P =99 %)
|
 Скачать 0.56 Mb.
Скачать 0.56 Mb.
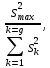 построенной по gнезависимым оценкам дисперсии (
построенной по gнезависимым оценкам дисперсии (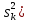 , каждая из которых обладает fстепенями свободы.
, каждая из которых обладает fстепенями свободы.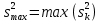 .;
.;
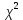 не превышает табличное. Это оцениваемое значение рассматривается как значимое (P1=95%) или как высоко значимое (P1=99%).
не превышает табличное. Это оцениваемое значение рассматривается как значимое (P1=95%) или как высоко значимое (P1=99%).