ОФС_Статистическая_обработка_результатов_физических__физико-хими. Статья статистическая обработка результатов физических, физикохимических и химических испытаний
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
1.6. Проверка наличия значимой систематической погрешности Для решения вопроса о наличии или отсутствии статистически значимой погрешности для выборки объема m, если величина 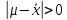 , используют критерий Стьюдента, обозначаемый tи рассчитываемый по формуле: , используют критерий Стьюдента, обозначаемый tи рассчитываемый по формуле:t = 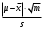 (1.38) (1.38)или для относительных величин: 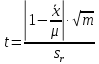 (1.38а) (1.38а)Если, например, при Р = 95 % и f = m − 1, реализуется неравенство: t > t (P, f), (1.39) то полученные данной методикой результаты отягощены систематической погрешностью, относительная величина которой δ может быть вычислена по формуле: 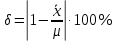 (1.40) (1.40)  Статистически значимая систематическая погрешность может быть приемлема для решения поставленной аналитической задачи, если она критически не влияет на принятие решения по результатам анализа. На статистическую значимость систематической погрешности влияет прецизионность. Вследствие высокой прецизионности систематическая погрешность может оказаться статистически значимой, и наоборот, низкая прецизионность может привести к статистической незначимости систематической погрешности (эффект маскировки). Предположим, что для методики 1 систематическая погрешность δ1 = 0,74 % и стандартное отклонение s1=1,20 %, а для методики 2 данные величины имеют значения δ2 = 0,37 % и s2=0,33 %. За счет худшей прецизионности систематическая погрешность методики 1 оказывается статистически незначимой. Лучшая прецизионность методики 2 приводит к статистической значимости систематической погрешности, несмотря на то, что ее значение меньше в 2 раза, чем у методики 1. Поэтому создается ложное представление о невозможности использования методики 2 для конкретной аналитической задачи, например, количественного определения действующего вещества в лекарственном препарате. В действительности, для данной цели целесообразно использовать именно методику 2. Таким образом, статистически значимая систематическая погрешность, может быть приемлемой и неприемлемой для решения поставленной аналитической задачи. В связи с этим статистически значимые систематические погрешности, т.е. погрешности, для которых выполняется неравенство (1.39), в дальнейшем оценивают на их практическую значимость. 2.Сравнение двух методик анализа по прецизионности Сравнение двух методик анализа по прецизионности проводят путем выяснения значимости различия выборочных дисперсий анализа этих двух методик. В более общем случае данный подход применяют для оценки значимости различия двух выборочных дисперсий, например, с целью выяснения, можно ли их считать выборочными оценками одной и той же дисперсии генеральной совокупности. При сравнении прецизионности двух методик анализа с оценками дисперсий 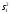 и и 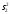 ( (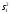 > > 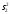 ) вычисляют критерий Фишера F: ) вычисляют критерий Фишера F:F = 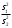 . (2.1) . (2.1)Критерий F характеризует при 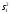 > > 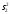 достоверность различия между достоверность различия между 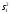 и и 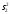 . . Вычисленное значение F сравнивают с табличным значением F(P, f1, f2), найденным при P1= 99 % (таблица 7.3. Приложения). Если для вычисленного значения F выполняется неравенство: F > F (P1, f1, f2), (2.2) то различие дисперсий 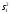 и и 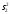 признается статистически значимым с вероятностью P1, что позволяет сделать заключение о более высокой прецизионности второй методики. признается статистически значимым с вероятностью P1, что позволяет сделать заключение о более высокой прецизионности второй методики. Если выполняется неравенство: F 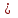 F(P1, f1, f2), (2.3) F(P1, f1, f2), (2.3)то различие значений 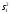 и и 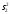 не может быть признано значимым и заключение о различии прецизионности (сходимости) методов сделать нельзя ввиду недостаточного объема информации. не может быть признано значимым и заключение о различии прецизионности (сходимости) методов сделать нельзя ввиду недостаточного объема информации.Если: F(P1=0,95, f1, f2) <F< F(P1=0,99, f1, f2), (2.4), то целесообразно провести дальнейшие экспериментальные исследования для методики с лучшей прецизионностью (сходимостью). При сравнении двух методик анализа результаты статистической обработки могут быть представлены в виде таблицы 2.1. Таблица 2.1 Данные для сравнительной статистической оценки двух методик анализа по прецизионности
Сравнение методик анализа желательно проводить при 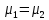 , f1> 10 и f2> 10. Если точные значения µ1 и µ2 неизвестны, величины δ и tвыч не определяют. , f1> 10 и f2> 10. Если точные значения µ1 и µ2 неизвестны, величины δ и tвыч не определяют.Если при измерениях получают логарифмы исходных вариант, то вместо величин µ,  иs в таблице 2.1. приводят величины lgµ, lg иs в таблице 2.1. приводят величины lgµ, lg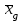 и и 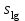 . При этом в графу 8 вносят величину . При этом в графу 8 вносят величину 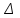 lgx, а в графу 9 – максимальное по абсолютной величине значение ε. Аналогичные замены проводят при вычислении t по уравнению (1.38) и F – по уравнению (3.1). lgx, а в графу 9 – максимальное по абсолютной величине значение ε. Аналогичные замены проводят при вычислении t по уравнению (1.38) и F – по уравнению (3.1).Пример сравнения двух методик анализа по прецизионности приведен в разделе 6.4. 3. Сравнение средних результатов выборок 3.1. Данные для сравнения результатов выборок Если с помощью данной методики анализа определяют значение некоторой величины А, то для экспериментально полученной однородной выборки объема m рассчитывают значения величин, приведенных в таблице 3.1. Если же для данной методики уже имеются данные для статистической обработки (например, полученные при сравнении методик по прецизионности, таблица 2.1), то в целях значительного сужения границ доверительного интервала за счет большего числа степеней свободы (уравнение 1.23) возможно их использование при заполнении граф 2, 4, 5, 7, 8 и 9 таблицы 3.1. Если 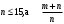 >1,5, величины s и f целесообразно вычислять по уравнениям (1.21) и (1.15). >1,5, величины s и f целесообразно вычислять по уравнениям (1.21) и (1.15).Таблица 3.1 Данные для сравнения средних результатов выборок
Во многих случаях проще использовать относительные (по отношению к  ) величины. В этом случае целесообразно использовать данные таблицы 3.2. ) величины. В этом случае целесообразно использовать данные таблицы 3.2.Таблица 3.2 Данные для сравнения средних результатов выборок с использованием относительных величин
Таким образом, на основании уравнения (1.21) для измеряемой величины А при незначительной систематической погрешности с вероятностью Р выполняется условие: 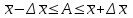 , (3.1) , (3.1)т. е., величина А при незначительной систематической погрешности лежит в пределах: A = 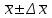 . (3.2) . (3.2)или с использованием относительных величин:  = 1± = 1±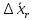 (3.2а) (3.2а) Если при измерениях получают логарифмы исходных вариант, в графе 9 таблицы 3.1 приводят величину 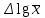 , а каждую из граф 3, 9 и 10 разбивают на две (а, б). В графе 3а приводят значение , а каждую из граф 3, 9 и 10 разбивают на две (а, б). В графе 3а приводят значение 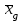 , в графе 3б – значение lg , в графе 3б – значение lg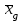 , в графах 9а и 9б – соответственно значения нижней и верхней границ доверительного интервала для , в графах 9а и 9б – соответственно значения нижней и верхней границ доверительного интервала для 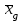 (уравнения (1.31) и (1.32)). Наконец, в графе 10 приводят максимальное по абсолютной величине значение (уравнения (1.31) и (1.32)). Наконец, в графе 10 приводят максимальное по абсолютной величине значение 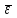 (уравнение (1.33а)). (уравнение (1.33а)). |

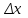
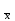
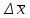 или
или