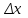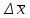ОФС_Статистическая_обработка_результатов_физических__физико-хими. Статья статистическая обработка результатов физических, физикохимических и химических испытаний
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Расчеты по уравнениям (1.2), (1.4), (1.5), (1.6) дали следующие результаты:  = 49,96; f = 9; s2 = 0,01366; s = 0,1169; s = 49,96; f = 9; s2 = 0,01366; s = 0,1169; s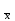 = 0,03696. = 0,03696.Доверительные интервалы результата отдельного определения и среднего результата при Р2 = 90 % получаем согласно (1.24) и (1.22): 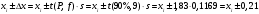 ; ;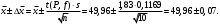 Тогда относительные неопределенности 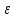 и и  , согласно (1.27) и (1.28), равны: , согласно (1.27) и (1.28), равны: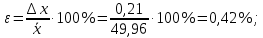 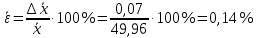 . .Обозначая истинное содержание действующего вещества в активной фармацевтической субстанции через µ, можно считать, что с 90 % доверительной вероятностью справедливы неравенства: 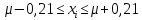 ; ;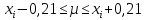 (при любом i); (при любом i);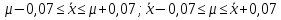 (при n = 10). (при n = 10).6.4.Сравнение двух методик анализа по прецизионности Пусть для двух выборок аналитических данных (1 и 2), характеризующих, например, различные методики анализа, получены данные для статистической обработки, приведенные в графах 1-10 таблицы 6.4. Таблица 6.4.
Для заполнения графы 10 вычисляем значения tвыч(1) и tвыч(2): 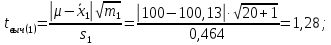 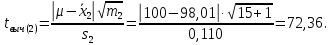 Поскольку tвыч(1) = 1,28 < t1 (95 %, 20) = 2,09, гипотеза 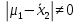 может быть отвергнута, что позволяет считать результаты выборки 1 свободными от систематической ошибки. может быть отвергнута, что позволяет считать результаты выборки 1 свободными от систематической ошибки.Напротив, поскольку tвыч(2) = 72,36 ≫ t2 (95 %, 15) = 2,13, гипотезу 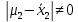 приходится признать статистически достоверной, что свидетельствует о наличии систематической ошибки в результатах выборки 2. В графу 13 вносим вычисленное значение δ2: приходится признать статистически достоверной, что свидетельствует о наличии систематической ошибки в результатах выборки 2. В графу 13 вносим вычисленное значение δ2: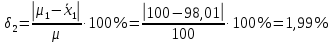 . .Заполним графы 11 и 12: F(99 %; 20; 15) = 3,36; F = 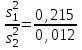 = 17,92; = 17,92;F = 17,92 ≫ F(99 %; 20;15) = 3,36. Следовательно, при Р1 = 99 % гипотезу о различии дисперсий 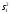 и и 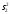 следует признать статистически достоверной. следует признать статистически достоверной.Выводы: - результаты, полученные при использовании первой методики, являются правильными, т.е. они не отягощены систематической погрешностью; - результаты, полученные при использовании второй методики, отягощены систематической погрешностью; - по прецизионности вторая методика существенно превосходит первую методику. 6.5.Сравнение средних результатов двух выборок При определении содержания действующего вещества в двух образцах лекарственного препарата, произведенных по разной технологии, получены данные для статистической обработки средних результатов, приведенные в таблице 6.5. Требуется определить, является ли первый образец по данному показателю лучшим в сравнении со вторым образцом. Таблица 6.5.
Поскольку F = 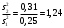 < F(99 %, 5,7) = 7,46, < F(99 %, 5,7) = 7,46, то согласно неравенству (2.3) статистически достоверное различие величин 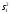 и и 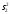 отсутствует. отсутствует.Следовательно, гипотеза 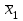 = =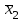 (3.3) проверяется с помощью уравнений (1.5), (1.7), (3.4) и (3.5). (3.3) проверяется с помощью уравнений (1.5), (1.7), (3.4) и (3.5).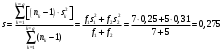 ; ;s = 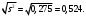 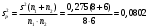 ; ;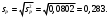 f = n1 + n2 – 2 = 8 + 6 – 2 = 12. 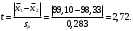 t = 2,72 > t(95 %; 12) = 2,18. t = 2,72 < t(99 %;12) = 3,08. Следовательно, с доверительной вероятностью Р2 = 95 % гипотеза 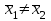 может быть принята (т.е. первый образец лучше второго по содержанию действующего вещества). Однако с доверительной вероятностью Р2=99 % принять эту гипотезу нельзя из-за недостатка информации. может быть принята (т.е. первый образец лучше второго по содержанию действующего вещества). Однако с доверительной вероятностью Р2=99 % принять эту гипотезу нельзя из-за недостатка информации.Если гипотеза 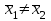 принята, то определяют доверительный интервал разности генеральных средних принята, то определяют доверительный интервал разности генеральных средних 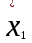 и и 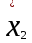 (уравнение (3.10)): (уравнение (3.10)):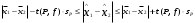 (Р2 = 95 %; f=12); 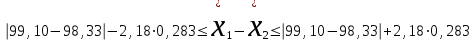 , ,0,15≤ 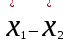 ≤ 1,39. ≤ 1,39.6.6. Расчет неопределенности результатов анализа лекарственных препаратов методом высокоэффективной жидкостной хроматографии В таблетке со средней массой 0,50 г содержание вещества А составляет 0,050 г. Для количественного определения вещества А методом высокоэффективной жидкостной хроматографии готовили испытуемый раствор: навеску m=0,5052 г порошка растертых таблеток поместили в мерную колбу вместимостью 50 мл и довели объем раствора растворителем до метки. Параллельно готовили раствор сравнения: 0,0508 г стандартного образца поместили в мерную колбу на 50 мл и довели объем раствора растворителем до метки. Попеременно хроматографировали испытуемый раствор и раствор сравнения, получая по 5 хроматограмм. Площади полученных пиков представлены в таблице 6.6. Таблица 6.6.
6.6.1.Конечная аналитическая операция Рассчитывают средние значения, содержание вещества А в одной таблетке и относительные стандартные отклонения площадей пиков для испытуемого раствора и раствора сравнения в конечной аналитической операции. Средние значения площадей пиков: - испытуемый раствор: (13957605+13806804+13924245+13715195+14059478)/5=13892665. - раствор сравнения: (14240777+14102192+14316388+14205217+14409585)/5=14254832. Содержание анализируемого вещества А в граммах в пересчете на среднюю массу таблетки: А= 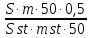 = =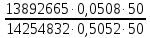 ·0,5= 0,0490. ·0,5= 0,0490.Относительные стандартные отклонения площадей пиков: - испытуемый раствор: RSD= 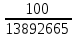 · ·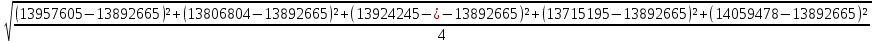 =0,97 %, =0,97 %,- аналогично для раствора сравнения: RSDst=0,81 % 6.6.2.Суммарная неопределенность пробоподготовки ΔSP,r Неопределенности: - неопределенность для мерной колбы вместимостью 50 мл ̶ не более 0,17 %; - неопределенность взвешивания на аналитических весах - не более 0,2 мг (0,0002 г), что составляет: 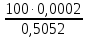 =0,04 % для испытуемого образца; =0,04 % для испытуемого образца;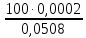 =0,39 % для стандартного образца. =0,39 % для стандартного образца.Данные неопределенности можно считать доверительными интервалами для вероятности 95 %. Суммарную неопределенность пробоподготовки рассчитывают по формуле (5.5): ΔSP,r= 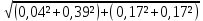 =0,46 %. =0,46 %.Приведенный расчет является корректным для обоих подходов - линейной модели и подхода Уэлча-Сатертуэйта, поскольку число степеней свободы для каждого члена здесь бесконечно, то используется статистика Гаусса. 6.6.3.Расчет суммарной неопределенности анализа ΔAs,r Данный расчет различен для линейной модели и подхода Уэлча-Сатертуэйта. 6.6.3.1. Линейная модель Общий случай. Рассчитывают неопределенности конечной аналитической операции ΔFAO,rдля испытуемого раствора и раствора сравнения. При расчете доверительных интервалов используют односторонний коэффициент Стьюдента для вероятности 95 % (равен 90 % для двустороннего распределения), который для числа степени свободы (5-1=4) равен 2,13. Доверительные интервалы рассчитывают для среднего из 5 результатов, поэтому в знаменателе ставим 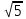 : :- для испытуемого: ΔsmpFAO,r = 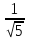 ·t(90%,4)·RSD= ·t(90%,4)·RSD=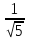 ·2,13·0,97=0,92 %. ·2,13·0,97=0,92 %.- для стандартного: ΔstFAO,r= 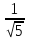 ·t(90%,4)·RSD= ·t(90%,4)·RSD=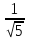 ·2,13·0,81=0,77 %. ·2,13·0,81=0,77 %.Суммарная неопределенность конечной аналитической операции: ΔFAO,r = 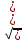 ΔsmpFAO,r)²+( ΔstFAO,r)² = ΔsmpFAO,r)²+( ΔstFAO,r)² =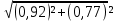 =1,2%. =1,2%.Используя уравнение (5.7), рассчитывают суммарную неопределенность анализа ΔAs,r: ΔAs,r= 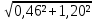 =1,29%. =1,29%.Использование объединенного стандартного отклонения. Суммарную неопределенность анализа можно уменьшить за счет использования объединенного стандартного отклонения для конечной аналитической операции. Для этого нужно учесть, что RSDиRSDstявляются выборочными величинами одной и той же генеральной совокупности. Проверяют вначале по Фишеру гипотезу о равенстве дисперсий: 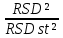 = =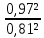 =1,434< 6,388 -F(P1 -95 %;4,4). =1,434< 6,388 -F(P1 -95 %;4,4).Как видно, расчетное значение отношения дисперсий гораздо ниже табличного значения F-критерия на 95 % уровне значимости. Поэтому можно принять гипотезу о равенстве дисперсий и принять формулы подраздела 1.4. настоящей общей фармакопейной статьи для объединения выборок. Рассчитывают объединенное стандартное отклонение по уравнению: RSDtot= 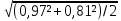 =0,89 %. =0,89 %.RSDtotимеет число степеней свободы 2·(5-1)=8. Коэффициент Стьюдента для данного числа степеней свободы и односторонней вероятности 0,95 равен 1,86. Тогда доверительные интервалы результатов конечной аналитической операции для испытуемого и стандартного растворов будут равны: ΔsmpFAO,r = ΔstFAO,r = 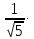 t(90 %;8)·RSD = t(90 %;8)·RSD =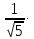 1,86·0,89 =0,74 %. 1,86·0,89 =0,74 %.Суммарная неопределенность конечной аналитической операции равна: ΔFAO,r = 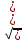 ΔsmpFAO,r)² + (ΔstFAO,r)² = ΔsmpFAO,r)² + (ΔstFAO,r)² = 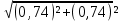 =1,05 %. =1,05 %.Используя уравнение (5.7) рассчитывают суммарную неопределенность анализа ΔAs,r: ΔAs,r= 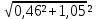 =1,15 %. =1,15 %.Как видно, данная величина меньше величины, полученной для обычного случая (1,29 %). 6.6.3.2.Подход Уэлча-Сатертуэйта Находят стандартное отклонение пробоподготовки из доверительного интервала ΔSP,r=0,83 %, используя коэффициент Гаусса 1,65 для односторонней вероятности 0,95 (поскольку число степеней свободы бесконечно, как для генеральной совокупности): SSP,r= 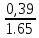 = 0,24 %. = 0,24 %.Из соотношения (5.5) найденное стандартное отклонение всей аналитической методики RSD² и (RSDst)² делят на 5, как для дисперсий среднего результата: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||