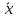ОФС_Статистическая_обработка_результатов_физических__физико-хими. Статья статистическая обработка результатов физических, физикохимических и химических испытаний
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
3.2. Сравнение средних результатов двух выборок Если в результате измерений одной и той же величины А получены две выборки объема n1 и n2, причем 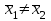 , может возникнуть необходимость проверки статистической достоверности гипотезы: , может возникнуть необходимость проверки статистической достоверности гипотезы: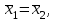 (3.3) (3.3)т. е. значимости величины разности ( 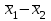 ). ).Такая проверка необходима, например, если величина А определялась двумя разными методиками с целью их сравнения, или, если величина А определялась одной и той же методикой для двух разных объектов, идентичность которых требуется доказать. Для проверки гипотезы (3.3) следует установить, существует ли статистически значимое различие между дисперсиями s 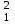 и s и s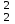 . Эта проверка проводится так же, как при сравнении двух методик анализа по воспоизводимости согласно уравнениям (2.1) - (2.3). . Эта проверка проводится так же, как при сравнении двух методик анализа по воспоизводимости согласно уравнениям (2.1) - (2.3).Рассматривают три случая. Различие дисперсий s 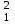 и s и s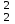 статистически незначимо, когда справедливо неравенство (2.3). В этом случае средневзвешенное значение s2, учитывающее не только количество выборок (дисперсий), но и их объем, вычисляют по уравнению (1.5), а дисперсию статистически незначимо, когда справедливо неравенство (2.3). В этом случае средневзвешенное значение s2, учитывающее не только количество выборок (дисперсий), но и их объем, вычисляют по уравнению (1.5), а дисперсию 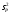 разности разности 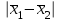 – по уравнению: – по уравнению: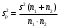 , (3.4) , (3.4)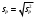 . (3.4a) . (3.4a)Далее вычисляют критерий Стьюдента: 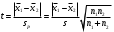 , (3.5) , (3.5)при f =n1+n2– 2.(3.5а) Если при выбранном значении Р2 (например, при Р2 = 95 %): t > t(P2, f), (3.6) то результат проверки положителен: разность ( 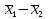 ) является значимой и гипотезу ) является значимой и гипотезу 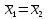 отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным. отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным.Различие дисперсий s 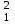 и s и s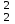 статистически значимо, когда справедливо неравенство (2.2). Если s статистически значимо, когда справедливо неравенство (2.2). Если s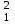 >s >s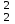 , дисперсию s , дисперсию s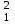 разности разности 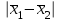 находят по уравнению (3.7), а число степеней свободы находят по уравнению (3.7), а число степеней свободы 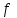 ' – по уравнению (3.8): ' – по уравнению (3.8):s 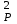 = = 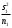 + + 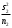 ; (3.7) ; (3.7)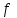 ' = (n1 + n2 – 2)(0,5 + ' = (n1 + n2 – 2)(0,5 + 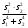 ). (3.8) ). (3.8)Следовательно, в данном случае: 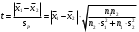 . (3.9) . (3.9)Вычисленное по уравнению (3.9) значение t сравнивают с табличным значением t (Р2, f ' ), как это описано выше для первого случая. Приведенные выше расчеты упрощаются, когда n1 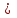 n2 и s n2 и s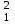 ≫s ≫s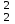 . Тогда в отсутствие систематической погрешности среднее . Тогда в отсутствие систематической погрешности среднее 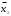 выборки объема n2 принимают за достаточно точную оценку величины А, т. е. принимают выборки объема n2 принимают за достаточно точную оценку величины А, т. е. принимают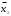 =µ. Справедливость гипотезы =µ. Справедливость гипотезы 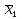 =µ, эквивалентной гипотезе (3.3), проверяют с помощью уравнений (1.38) и (1.39), принимая f1=n1–1. Гипотеза (3.3) отклоняется как статистически недостоверная, если выполнятся неравенство (1.39). =µ, эквивалентной гипотезе (3.3), проверяют с помощью уравнений (1.38) и (1.39), принимая f1=n1–1. Гипотеза (3.3) отклоняется как статистически недостоверная, если выполнятся неравенство (1.39).Известно точное значение величины А. Если A=µ, проверяют две гипотезы: 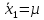 и и 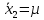 .Проверку выполняют с помощью уравнений (1.38) и (1.39) отдельно для каждой из гипотез. Если обе проверяемые гипотезы статистически достоверны, то следует признать достоверной и гипотезу (3.3). В противном случае гипотеза (3.3) должна быть отброшена. .Проверку выполняют с помощью уравнений (1.38) и (1.39) отдельно для каждой из гипотез. Если обе проверяемые гипотезы статистически достоверны, то следует признать достоверной и гипотезу (3.3). В противном случае гипотеза (3.3) должна быть отброшена. Если при измерениях получают логарифмы исходных вариант, при сравнении средних используют величины 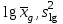 и и 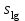 .В тех случаях, когда разность .В тех случаях, когда разность 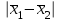 оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних | оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних |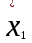 и и 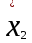 | : | :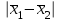 – t(P, f) – t(P, f)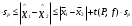 . (3.10) . (3.10)Пример сравнения средних результатов двух выборок приведен в разделе 6.5. 4. Расчет и статистическая оценка параметров линейной зависимости При использовании физических, физико-химических и химических методов анализа для количественного определения веществ непосредственному измерению подвергается некоторая величина у (аналитический сигнал), которая является, как правило, линейной функцией искомой концентрации (количества) х определяемого вещества или элемента. Иными словами, в основе таких методов анализа лежит экспериментально подтвержденная линейная зависимость: y = bx + a, (4.1); где: у ‒ измеряемая величина (измеряемое значение аналитического сигнала); х ‒ концентрация (количество) определяемого вещества или элемента; b ‒угловой коэффициент линейной зависимости; а ‒ свободный член линейной зависимости. (Здесь b и а рассматривают как коэффициенты (параметры) линейной регрессии y на x). Для использования зависимости (4.1) в аналитических целях, т. е. для определения конкретной величины х по измеренному значению у, необходимо заранее найти числовые значения констант b и а,т.е. провести калибровку. Иногда константы зависимости (4.1) имеют тот или иной физический смысл, и их значения должны оцениваться с учетом соответствующего доверительного интервала. Если калибровка проведена и значения констант а и b определены, величину хi находят по измеренному значению yi: хi = 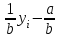 . (4.2) . (4.2)При калибровке величину х рассматривают как аргумент, а величину у – как функцию. Наличие линейной зависимости между х и у не всегда является очевидным, ее наличие целесообразно подтверждать расчетным путем. Для этого по экспериментальным данным, полученным при калибровке, оценивают достоверность линейной связи между х и у с использованием корреляционного анализа и лишь затем рассчитывают значения констант а и b зависимости (6.1) и их доверительные интервалы. В первом приближении судить о достоверности линейной связи между переменными х и у можно по величине линейного коэффициента корреляции (или просто коэффициента корреляции) r, который вычисляют по формуле, исходя из экспериментальных данных: 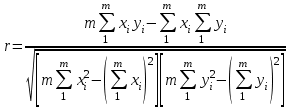 (4.3) (4.3)Линейный коэффициент корреляции rизменяется в пределах от -1 до +1.Положительные значенияrуказывают на рост, а негативные - на уменьшение у с ростом х. Линейный коэффициент корреляции rявляется частным случаем общего индекса корреляцииRc,который применим также и для нелинейных зависимостей между величинами у и х: Rc= 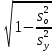 (4.3а), (4.3а), где: so – остаточное стандартное отклонение (стандартное отклонение линейной зависимости) (уравнение 4.7); sy – стандартное отклонение величин у относительно среднего значения 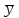 ( 4.15); рассчитывают с использованием уравнения (1.5). ( 4.15); рассчитывают с использованием уравнения (1.5).Уравнение (4.3а) в силу своей простоты и наглядности нередко используют вместо уравнения (4.3) в том случае, когда знак коэффициента корреляции не имеет значения. Чем ближе абсолютная величина 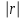 к единице, тем менее случайна наблюдаемая линейная зависимость между переменными х и у. Коэффициент корреляции r используют обычно для выявления стохастической взаимосвязи между величинами, функциональная зависимость между которыми может и отсутствовать. Коэффициент корреляции является значимым, если его величина для данной вероятности Р и числа степенейсвободы fпревышает значения, приведенные таблице 7.4. Приложения. В противном случае нельзя говорить о существовании значимых зависимостей (4.1) - (4.2). к единице, тем менее случайна наблюдаемая линейная зависимость между переменными х и у. Коэффициент корреляции r используют обычно для выявления стохастической взаимосвязи между величинами, функциональная зависимость между которыми может и отсутствовать. Коэффициент корреляции является значимым, если его величина для данной вероятности Р и числа степенейсвободы fпревышает значения, приведенные таблице 7.4. Приложения. В противном случае нельзя говорить о существовании значимых зависимостей (4.1) - (4.2).Значимость коэффициента корреляции является обязательным, но не достаточным условием использования уравнений (4.1) - (4.2) в для аналитических целей. При статистической обработке результатов физического, физико-химического или химического методов анализа лекарственных средств могут быть использованы линейные зависимости с коэффициентом корреляции 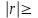 0,98 (при соответствии требованиям таблицы 7.4. Приложения ), а при анализе следовых количеств определяемых веществ рассматривают линейные зависимости с коэффициентом корреляции 0,98 (при соответствии требованиям таблицы 7.4. Приложения ), а при анализе следовых количеств определяемых веществ рассматривают линейные зависимости с коэффициентом корреляции 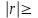 0,90. При столь близких значениях величины 0,90. При столь близких значениях величины 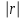 к единице формальное подтверждение наличия линейной связи между переменными x и y проводить не следует. Вместе с тем необходимо учитывать, что для различных методов анализа лекарственных средств, требования к линейности метода, могут быть различными. к единице формальное подтверждение наличия линейной связи между переменными x и y проводить не следует. Вместе с тем необходимо учитывать, что для различных методов анализа лекарственных средств, требования к линейности метода, могут быть различными. Коэффициенты а и b и другие характеристики линейной зависимости (4.1) рассчитывают с использованием регрессионного анализа, т. е. методом наименьших квадратов по экспериментально измеренным значениям переменной у для заданных значений аргумента х. Пусть в результате эксперимента найдены представленные в таблице 4.1 пары значений аргумента х и функции у. Таблица 4.1 Значения аргумента х и функции у.
Тогда, если величины у1 имеют одинаковую неопределенность (а такое допущение обычно выполняется для достаточно узкого диапазона варьирования величин у1), то 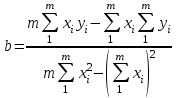 , (4.4) , (4.4)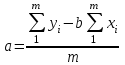 , (4.5) , (4.5)f = m – 2. (4.6) Если полученные значения коэффициентов а и b использовать для вычисления значений у по заданным в таблице 4.1 значениям аргумента х согласно зависимости (4.1), то вычисленные значения у обозначают через Y1, Y2, ... , Yi, ... Yn. Разброс значений уiотносительно значений Yi характеризует величина остаточной дисперсии s 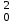 (дисперсии линейной зависимости), которую вычисляют по формуле: (дисперсии линейной зависимости), которую вычисляют по формуле: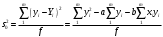 . (4.7) . (4.7)Для того, чтобы уравнения (4.1) - (4.2) адекватно описывали экспериментальные данные, необходимо, чтобы остаточная дисперсия 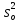 не отличалась значимо по критерию Фишера (уравнения (2.1) и (2.2)) от дисперсии прецизионности величин у1. Последняя может быть найдена или спрогнозирована из паспортных данных оборудования. не отличалась значимо по критерию Фишера (уравнения (2.1) и (2.2)) от дисперсии прецизионности величин у1. Последняя может быть найдена или спрогнозирована из паспортных данных оборудования.В свою очередь, дисперсии констант b и а находят по уравнениям: s 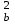 = = 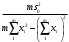 ; (4.8) ; (4.8)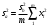 . (4.9) . (4.9)Стандартные отклонения sb и sa и величины 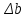 и и 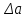 , необходимые для оценки доверительных интервалов констант уравнения регрессии, рассчитывают по уравнениям: , необходимые для оценки доверительных интервалов констант уравнения регрессии, рассчитывают по уравнениям: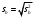 ; (4.10) ; (4.10)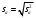 ; (4.11) ; (4.11)∆b = t(P,f)∙sb; (4.12) ∆a = t(P,f)∙sa. (4.13) Коэффициенты а и b должны значимо отличаться от нуля, т.е. превышать, соответственно, величины ∆a и ∆b. Уравнению (4.1) с константами а и b обязательно удовлетворяет точка с координатами  и и 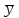 , называемая центром калибровочного графика: , называемая центром калибровочного графика: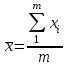 ; (4.14) ; (4.14)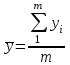 . (4.15) . (4.15)Наименьшие отклонения значений yi от значений Yi наблюдаются в окрестностях центра графика. Стандартные отклонения sy и sx величин у и х, рассчитанных соответственно по уравнениям (4.1) и (4.2), исходя соответственно из известных значений х и у, определяют с учетом удаления последних от центра графика: 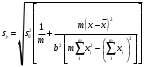 ; (4.16) ; (4.16)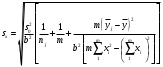 , (4.17) , (4.17)где 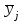 – среднее значение; – среднее значение;nj– число вариант y, использованных при определении 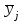 . .При x =  и и 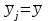 выражения (4.16) и (4.17) принимают вид: выражения (4.16) и (4.17) принимают вид: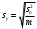 ; (4.16а) ; (4.16а)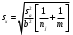 . (4.17а) . (4.17а)С учетом значений sy и sx могут быть найдены значения величин ∆y и ∆x: ∆y = sy∙t(P, f); (4.18) ∆x = sx∙t(P, f). (4.19) Значения sx и ∆x, найденные при nj = 1, являются характеристиками прецизионности аналитической методики, если х – концентрация (количество), а у – функция х. Обычно результаты статистической обработки по методу наименьших квадратов сводят в таблицу (таблица 4.2.). Таблица 4.2. Результаты статистической обработки экспериментальных данных, полученных при изучении линейной зависимости у = bx + a
Примечания: 1.Если целью экспериментальной работы являлось определение констант b и a, графы 11, 12 и 13 таблицы не заполняют 2. 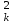 Если y = b∙lgx + a, вычисления, описанные в настоящем разделе, выполняют с использованием уравнений (1.8), (1.9), (1.29)-(1.32). 3. Сравнение дисперсий 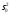 , полученных в разных условиях для двух линейных зависимостей, может быть проведено, как указано в разделе 2. , полученных в разных условиях для двух линейных зависимостей, может быть проведено, как указано в разделе 2.5. Расчет неопределенности функции нескольких случайных переменных Описанные в разделах 1-4 настоящей общей фармакопейной статьи расчеты доверительных интервалов результатов методик анализа применимы лишь в том случае, если измеряемая величина (концентрация, содержание и т.д.) является функцией только одной случайной переменной. Однако большинство методик количественного определения при испытании лекарственных средств методами физического, физико-химического и химического анализа являются косвенными, то есть используют стандартные образцы. Следовательно, измеряемая величина является функцией, как минимум, двух случайных переменных – аналитических сигналов (оптическая плотность или поглощение, высота или площадь пика и т.д.) испытуемого и стандартного образцов. Кроме того, нередко возникает проблема прогнозирования неопределенности аналитической методики, состоящей из нескольких стадий (взвешивание, разведение, конечная аналитическая операция), каждая из которых является по отношению к другой случайной величиной. Таким образом, возникает общая проблема оценки неопределенности косвенно измеряемой величины, зависящей от нескольких измеряемых величин, в частности, как рассчитывать неопределенность всей аналитической методики, если известны неопределенности отдельных ее составляющих (стадий)? Если измеряемая на опыте величина у является функцией п независимых случайных величин хi, то есть: (5.1) и число степеней свободы величин xiодинаково или достаточно велико (> 30, чтобы можно было применять статистику Гаусса, а не Стьюдента), то дисперсия величины у связана с дисперсиями величин xiсоотношением (правило распространения неопределенностей): 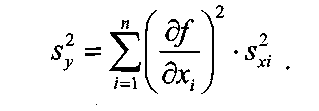 (5.2) (5.2)Однако на практике степени свободы величин xtобычно невелики и не равны друг другу. Кроме того, обычно интерес представляют не сами дисперсии (стандартные отклонения), а доверительные интервалы, рассчитать которые, используя уравнение (5.2), при небольших и неодинаковых степенях свободы невозможно. Поэтому для расчета неопределенности величины у (Δу) предложены различные подходы, среди которых можно выделить два основных: линейная модель и подход Уэлча–Сатертуэйта. 5.1 Линейная модель Если случайные переменные хiстатистически независимы, то доверительный интервал функции Δусвязан с доверительными интервалами переменных Δxiсоотношением (доверительные интервалы берутся для одной и той же вероятности): 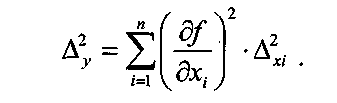 (5.3) (5.3)Данное выражение является обобщением соотношения (5.2). При испытании лекарственных средств методами физического, физико-химического и химического методами анализа измеряемая величина у представляет собой обычно произведение или частное случайных и постоянных величин (масс навесок, разведений, поглощений или площадей пиков и т.д.), т.е. (К ‒некая константа): 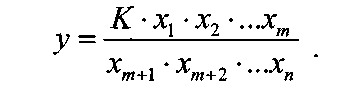 (5.4) (5.4) В этом случае соотношение (4.2) принимает вид: 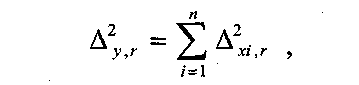 (5.5) (5.5)где использованы относительные доверительные интервалы. Соотношение (5.4) применимо при любых (разных) степенях свободы (в том числе и бесконечных) для величин xi. Его преимуществом является простота и наглядность. Использование абсолютных доверительных интервалов приводит к гораздо более громоздким выражениям, поэтому рекомендуется использовать относительные величины. При проведении испытаний лекарственных средств в суммарной неопределенности (ΔAS:r) анализа обычно всегда можно выделить такие типы неопределенностей: неопределенность пробоподготовки (ΔSPr), неопределенность конечной аналитической операции (ΔFAO,r) и неопределенность аттестации стандартного образца (ΔRS,r). Величина ΔRS,r обычно мала, поэтому в приведенном выражении она не использована. Учитывая это, а также то, что анализ проводится и для испытуемого раствора (индекс «smp»), и для раствора сравнения (индекс «st»), выражение (5.5) можно представить в виде: При этом каждое из слагаемых рассчитывают из входящих в него компонентов по уравнению (5.5). Если число степеней свободы величин хiодинаково или достаточно велико (> 30), выражение (5.5) дает: 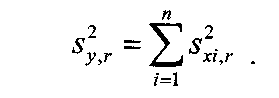 (5.7) (5.7)Это же соотношение получают при тех же условиях и из выражения (5.2). 5.2. Подход Уэлча-Сатертуэйта В этом подходе дисперсию величины у (s2у) рассчитывают по соотношению (5.2), не обращая внимания на различие в степенях свободы (νi) величин xiДля полученной дисперсии s2у рассчитывают некое «эффективное» число степеней свободы veff(которое обычно является дробным), на основе которого затем по таблицам для заданной вероятности находят интерполяцией значения критерия Стьюдента. На основе его далее рассчитывают обычным путем доверительный интервал величины у (Δу): 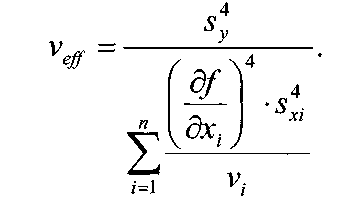 (5.8) (5.8)Для определения величины у обычно выполняется уравнение (5.4). В этом случае в подходе Уэлча–Сатертуэйта соотношение (5.2) переходит в выражение (5.7), и соотношение (5.8) принимает более простой вид: 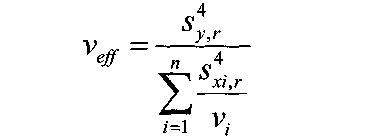 (5.9) (5.9)Здесь величину sy,r4 рассчитывают из соотношения (4.7). Подход Уэлча–Сатертуэйта обычно дает более узкие доверительные интервалы, чем линейная модель. Однако он гораздо сложнее в применении и не позволяет выделить так просто неопределенности разных этапов (с последующими рекомендациями по их минимизации), как линейная модель в форме выражения (5.6). При прогнозе неопределенности анализа используют генеральные величины (с бесконечным числом степеней свободы). В этом случае подход Уэлча–Сатертуэйта совпадает с линейной моделью. Пример расчета неопределенности функции нескольких переменных приведен в разделе 6.6. 6. Примеры статистической обработки результатов испытаний 6.1. Вычисление среднего значения и дисперсии При количественном определении действующего вещества в образце лекарственного препарата, были получены данные, указанные в таблице 6.1. Таблица 6.1.
n = 5; f = n – 1 = 5 – 1 = 4.  = = 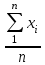 = = 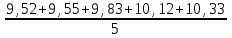 = 9,87. = 9,87.di = 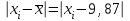 , , т. е. di=1 = 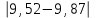 = 0,35и т. д. до i = 5. = 0,35и т. д. до i = 5.s2 = 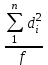 = = 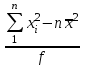 = = 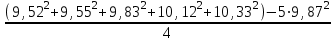 = 0,1252; = 0,1252;s = 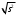 = = 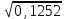 = 0,3538; = 0,3538;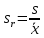 = = 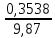 =0,03585; =0,03585;RSD = sr ·  100 %=3,59%; 100 %=3,59%;s 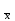 = = 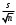 = = 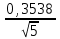 =0,1582; =0,1582;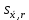 = = 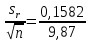 =0,01603; =0,01603;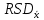 = = 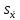 ,r ·100 %=1,60%. ,r ·100 %=1,60%.6.2. Проверка однородности выборки малого объема При количественном определении действующего вещества в каждой из девяти (n = 9) выборок лекарственного препарата были получены данные, указанные в таблице 6.2 (в порядке возрастания). Таблица 6.2.
По уравнениям (1.10б) и (1.11а) находим: R = 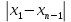 = = 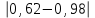 =0,36; =0,36;Q1 = 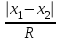 = = 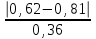 = 0,53. = 0,53.По таблице 7.1. Приложения находим: Q(9; 95%) = 0,46 < Q1 = 0,53; Q(9; 99%) = 0,55 > Q1 = 0,53. Следовательно, гипотеза о том, что значение x1=0,62 должно быть исключено из рассматриваемой совокупности результатов измерений как отягощенное грубой погрешностью, может быть принята с доверительной вероятностью 95 %, но должна быть отвергнута, если выбранное значение доверительной вероятности равно 99 %. 6.3.Вычисление доверительных интервалов и неопределенностей измерений При определении количественного содержания действующего вещества в образце активной фармацевтической субстанции были получены данные (n = 10), указанные в таблице 6.3. Таблица 6.3.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

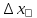
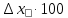 )
)