1.1.13 отчет. 1.1.13._(ОФС.1.1.0013.15). Статья статистическая обработка результатов офс 0013. 15
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ОБЩАЯ ФАРМАКОПЕЙНАЯ СТАТЬЯ Статистическая обработка результатов ОФС.1.1.0013.15 химического эксперимента Взамен ст. ГФ XI, вып.1 Требования данной общей фармакопейной статьи распространяются на методы, используемые при статистической обработке результатов химического эксперимента. Обозначения: А – измеряемая величина; a – свободный член линейной зависимости; b– угловой коэффициент линейной зависимости; F– критерий Фишера; f – число степеней свободы; i – порядковый номер варианты; L – фактор, используемый при оценке сходимости результатов параллельных определений; т, п – объемы выборки; P, 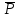 – доверительная вероятность соответственно при дву- и – доверительная вероятность соответственно при дву- иодносторонней постановке задачи; Q1, Qn– контрольные критерии идентификации грубых ошибок; R– размах варьирования; r– коэффициент корреляции; s– стандартное отклонение; s2– дисперсия; s 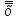 – стандартное отклонение среднего результата; – стандартное отклонение среднего результата;s 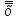 ,% – относительное стандартное отклонение среднего результата ,% – относительное стандартное отклонение среднего результата (коэффициент вариации); slg – логарифмическое стандартное отклонение; s2lg – логарифмическая дисперсия; slg 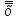 g – логарифмическое стандартное отклонение среднего g – логарифмическое стандартное отклонение среднегогеометрического результата; s 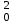 , s , s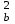 , s , s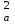 – общая дисперсия и дисперсия коэффициентов линейной – общая дисперсия и дисперсия коэффициентов линейнойзависимости; t – критерий Стьюдента; U – коэффициент для расчета границ среднего результата гарантии качества анализируемого продукта; х, у – текущие координаты в уравнении линейной зависимости; Хi, Yi – вычисленные, исходя из уравнения линейной зависимости, значения переменных х и у;  , , 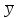 – средние выборки (координаты центра линейной зависимости); – средние выборки (координаты центра линейной зависимости);хi,, yi – i-тая варианта (i-тая пара экспериментальных значений х и у);  ± ∆ ± ∆ – граничные значения доверительного интервала среднего – граничные значения доверительного интервала среднегорезультата; хi ± ∆х– граничные значения доверительного интервала результата отдельного определения; d, ∆ – разность некоторых величин; – уровень значимости, степень надежности; ∆х– полуширина доверительного интервала величины; δ – относительная величина систематической ошибки; ε, 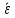 – относительные ошибки соответственно результата отдельного – относительные ошибки соответственно результата отдельногоопределения и среднего результата; µ – истинное значение измеряемой величины; ∑ – знак суммирования (сумма); X2 – критерий хи-квадрат. Примечание. Термины доверительная вероятностьP и уровень значимости (степень надежности) взаимозаменяемы, поскольку их сумма равна либо 1, либо 100 %. Метрологические характеристики методов и результатов, получаемых при статистической обработке данных эксперимента, позволяют проводить оценку и сравнение, как методик аналитического эксперимента, так и исследуемых при таком эксперименте объектов, и на этой основе решать ряд прикладных задач. 1. Основные статистические характеристики однородной выборки и их вычисление Проверка однородности выборки. Исключение выпадающих значений вариант. Термином «выборка» обозначают совокупность статистически эквивалентных найденных в эксперименте величин (вариант). В качестве такой совокупности можно, например, рассматривать ряд результатов, полученных при параллельных определениях содержания какого-либо вещества в однородной по составу пробе. Допустим, что отдельные значения вариант выборки объема п обозначены через xi (1 ≤ i ≤ n) и расположены в порядке возрастания: x1; х2; ... хi; ...хn-1; хn. (1.1) Результаты, полученные при статистической обработке выборки, будут достоверны лишь в том случае, если эта выборка однородна, т. е. если варианты, входящие в нее, не отягощены грубыми ошибками, допущенными при измерении или расчете. Такие варианты должны быть исключены из выборки перед окончательным вычислением ее статистических характеристик. Для выборки небольшого объема (n < 10) идентификация вариант, отягощенных грубыми ошибками, может быть выполнена, исходя из величины размаха варьирования R,см. уравнения (1.12), (1.13). Для идентификации таких вариант в выборке большого объема (n 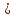 10) целесообразно проводить предварительную статистическую обработку всей выборки, полагая ее однородной, и уже затем на основании найденных статистических характеристик решать вопрос о справедливости сделанного предположения об однородности, см. выражение (1.14). 10) целесообразно проводить предварительную статистическую обработку всей выборки, полагая ее однородной, и уже затем на основании найденных статистических характеристик решать вопрос о справедливости сделанного предположения об однородности, см. выражение (1.14).В большинстве случаев среднее выборки 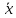 является наилучшей оценкой истинного значения измеряемой величины µ, если его вычисляют как среднее арифметическое всех вариант: является наилучшей оценкой истинного значения измеряемой величины µ, если его вычисляют как среднее арифметическое всех вариант: = = 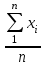 . (1.2) . (1.2)При этом разброс вариант хiвокруг среднего 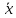 характеризуется величиной стандартного отклонения s. В количественном химическом анализе величина s часто рассматривается как оценка случайной ошибки, свойственной данному методу анализа. Квадрат этой величины s2 называют дисперсией. Величина дисперсии может рассматриваться как мера воспроизводимости результатов, представленных в данной выборке. Вычисление величин (оценок) s и s2 проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений di и число степеней свободы (число независимых вариант) f: характеризуется величиной стандартного отклонения s. В количественном химическом анализе величина s часто рассматривается как оценка случайной ошибки, свойственной данному методу анализа. Квадрат этой величины s2 называют дисперсией. Величина дисперсии может рассматриваться как мера воспроизводимости результатов, представленных в данной выборке. Вычисление величин (оценок) s и s2 проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений di и число степеней свободы (число независимых вариант) f:di= xi–  , (1.3) , (1.3)f = n – 1, (1.4) s2 = 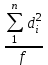 = = 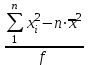 , (1.5) , (1.5)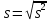 (1.6) (1.6)Стандартное отклонение среднего результата s 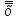 рассчитывают рассчитываютпо уравнению: 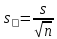 (1.7) (1.7)Отношение s 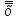 к к  , выраженное в процентах, называют относительным стандартным отклонением среднего результата или коэффициентом вариации s , выраженное в процентах, называют относительным стандартным отклонением среднего результата или коэффициентом вариации s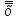 , %. , %.Примечание 1.1. При наличии ряда из gвыборок с порядковыми номерами k(1 ≤ k≤ g) расчет дисперсии s целесообразно проводить по формуле: s2 = 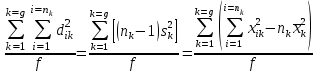 . (1.8) . (1.8)При этом число степеней свободы равно: f = 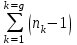 , (1.9) , (1.9)где xk – среднее k-той выборки; nk– число вариант в k-тойвыборке; xik– i-тая варианта k-той выборки; s 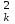 – дисперсия k-той выборки; – дисперсия k-той выборки;dik – отклонение i-той варианты k-той выборки. Необходимым условием применения уравнений (1.8) и (1.9) является отсутствие статистически достоверной разницы между отдельными значениями s 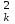 . В простейшем случае сравнение крайних значений s . В простейшем случае сравнение крайних значений s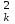 проводят, исходя из величины критерия F, которую вычисляют по уравнению (3.4) и интерпретируют, как указано в разделе 3. проводят, исходя из величины критерия F, которую вычисляют по уравнению (3.4) и интерпретируют, как указано в разделе 3.Примечание 1.2. Если при измерениях получают логарифмы искомых вариант, среднее выборки вычисляют как среднее геометрическое, используя логарифм вариант: lg  g = g = 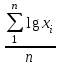 , (1.10) , (1.10)откуда  g = g = 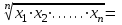 antilg (lg antilg (lg g).(1.11) g).(1.11)Значения s2, s и s 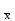 в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через s в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через s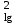 , slg и slg , slg и slg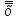 g. g.Пример 1.1. При определении содержания стрептоцида в образце линимента были получены следующие данные:
n = 5; f = n – 1 = 5 – 1 = 4. x = 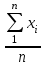 = = 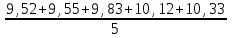 = 9,87. = 9,87.di = 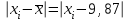 , т. е. di=1 = , т. е. di=1 = 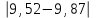 = 0,35и т. д. до i = 5. = 0,35и т. д. до i = 5.s2 = 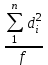 = = 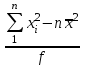 = = 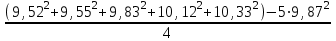 = = = 0,1252; s = 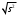 = = 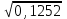 = 0,3538; = 0,3538;s 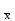 = = 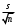 = = 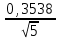 =0,1582. =0,1582. Как было указано выше, значения х, s2, s и s 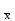 могут быть признаны достоверными, если ни одна из вариант выборки не отягощена грубой ошибкой, т. е. если выборка однородна. Проверка однородности выборок малого объема (n< 10) осуществляется без предварительного вычисления статистических характеристик, с этой целью после представления выборки в виде (1.1) для крайних вариант x1 и xn рассчитывают значения контрольного критерия Q, исходя из величины размаха варьирования R: могут быть признаны достоверными, если ни одна из вариант выборки не отягощена грубой ошибкой, т. е. если выборка однородна. Проверка однородности выборок малого объема (n< 10) осуществляется без предварительного вычисления статистических характеристик, с этой целью после представления выборки в виде (1.1) для крайних вариант x1 и xn рассчитывают значения контрольного критерия Q, исходя из величины размаха варьирования R:R = 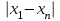 , (1.12) , (1.12)Q1 = 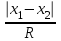 , (1.13 а) , (1.13 а)Qn= 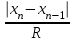 . (1.13 б) . (1.13 б)Выборка признается неоднородной, если хотя бы одно из вычисленных значений Q превышает табличное значение Q ( 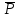 , n), найденное для доверительной вероятности , n), найденное для доверительной вероятности 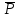 (см. табл. I приложения). Варианты х1 или xn, для которых соответствующее значение Q > Q( (см. табл. I приложения). Варианты х1 или xn, для которых соответствующее значение Q > Q(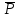 , n), отбрасываются и для полученной выборки уменьшенного объема выполняют новый цикл вычислений по уравнениям (1.12) и (1.13) с целью проверки ее однородности. Полученная в конечном счете однородная выборка используется для вычисления х, s2, s и s , n), отбрасываются и для полученной выборки уменьшенного объема выполняют новый цикл вычислений по уравнениям (1.12) и (1.13) с целью проверки ее однородности. Полученная в конечном счете однородная выборка используется для вычисления х, s2, s и s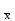 . .Примечание 1.3. При 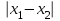 < < 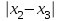 и и 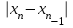 < < 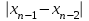 уравнения (1.13 а) и (1.13 б) принимают соответственно вид: уравнения (1.13 а) и (1.13 б) принимают соответственно вид:Q1 = 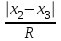 ; Qn = ; Qn = 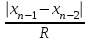 . .Пример1.2. При проведении девяти (n = 9) определений содержания общего азота в плазме крови крыс были получены следующие данные (в порядке возрастания):
По уравнениям (1.12) и (1.13 а) находим: R = 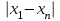 = = 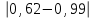 =0,37; =0,37;Q1 = 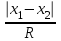 = = 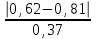 = 0,51. = 0,51.По табл. I приложения находим: Q(9; 95%) = 0,46 < Q1 = 0,51; Q(9; 99%) = 0,55 > Q1 = 0,51. Следовательно, гипотеза о том, что значение x1 = 0,62 должно быть исключено из рассматриваемой совокупности результатов измерений как отягощенное грубой ошибкой, может быть принята с доверительной вероятностью 95 %, но должна быть отвергнута, если выбранное значение доверительной вероятности равно 99 %. Для выборок большого объема (n 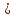 10) проверку однородности проводят после предварительного вычисления статистических характеристик 10) проверку однородности проводят после предварительного вычисления статистических характеристик  , s2, s и s , s2, s и s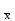 . При этом выборка признается однородной, если для всех вариант выполняется условие: . При этом выборка признается однородной, если для всех вариант выполняется условие: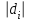 ≤ 3s. (1.14) ≤ 3s. (1.14)Если выборка признана неоднородной, то варианты, для которых |di| > 3s, отбрасываются как отягощенные грубыми ошибками с доверительной вероятностью Р > 99,0 %. В этом случае для полученной выборки сокращенного объема повторяют цикл вычислений статистических характеристик по уравнениям (1.2), (1.5), (1.6), (1.9) и снова проводят проверку однородности. Вычисление статистических характеристик считают законченным, когда выборка сокращенного объема оказывается однородной. Примечание 1.4. При решении вопроса об однородности конкретной выборки небольшого объема также можно воспользоваться выражением (1.14), если известна оценка величины s, ранее найденная для данного метода измерения (расчета) вариант. 2. Доверительные интервалы и оценка их величины Если случайная однородная выборка конечного объема n получена в результате последовательных измерений некоторой величины А, имеющей истинное значение µ, то среднее этой выборки  следует рассматривать лишь как приближенную оценку величины А. Достоверность этой оценки характеризуется величиной доверительного интервала следует рассматривать лишь как приближенную оценку величины А. Достоверность этой оценки характеризуется величиной доверительного интервала 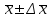 , для которой с заданной доверительной вероятностью Р выполняется условие: , для которой с заданной доверительной вероятностью Р выполняется условие: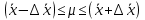 . (2.1) . (2.1)Следует отметить, что данный доверительный интервал не характеризует погрешность определения величины µ, поскольку найденная величина 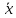 может быть в действительности очень близка к истинному значению µ. Полученный доверительный интервал характеризует степень неопределенности истинного значения µвеличины А по результатам последовательных измерений выборки конечного объема n. Поэтому правильно говорить о «неопределенности результатов анализа» (которая характеризуется доверительным интервалом) вместо выражения «погрешность результатов анализа», которое нередко не совсем корректно используется. может быть в действительности очень близка к истинному значению µ. Полученный доверительный интервал характеризует степень неопределенности истинного значения µвеличины А по результатам последовательных измерений выборки конечного объема n. Поэтому правильно говорить о «неопределенности результатов анализа» (которая характеризуется доверительным интервалом) вместо выражения «погрешность результатов анализа», которое нередко не совсем корректно используется.Расчет граничных значений доверительного интервала проводят по критерию Стьюдента, предполагая, что варианты, входящие в выборку, распределены нормально: 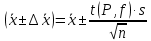 . (2.2) . (2.2)Здесь t (P, f) – табличное значение критерия Стьюдента (см. табл. II приложения). Если при измерении одним и тем же методом двух близких значений А были получены две случайные однородные выборки с объемами n и m, то при m < n для выборки объема m справедливо выражение: 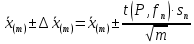 , (2.3) , (2.3)где индекс указывает принадлежность величин к выборке объема mили n. Выражение (2.3) позволяет оценить величину доверительного интервала среднего 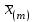 , найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего , найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего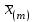 для выборки относительно малого объема m может быть сужен благодаря использованию известных величин s(n) и t(P, f(n)), найденных ранее для выборки большего объема n (в дальнейшем индекс n будет опущен). для выборки относительно малого объема m может быть сужен благодаря использованию известных величин s(n) и t(P, f(n)), найденных ранее для выборки большего объема n (в дальнейшем индекс n будет опущен).Примечание 2.1. Если 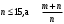 >1,5, величины s и f целесообразно вычислять, как указано в примечании 1.1. >1,5, величины s и f целесообразно вычислять, как указано в примечании 1.1.Подставляя n= 1 в выражение (2.2), или m = 1 в выражение (2.3), получаем: 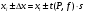 . (2.4) . (2.4)Этот интервал является доверительным интервалом результата единичного определения. Для него с доверительной вероятностью Р выполняются взаимосвязанные условия: xi – 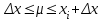 , (2.5) , (2.5)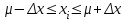 . (2.6) . (2.6)Значения 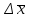 и и 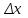 из выражений (2.2) и (2.4) используют при вычислении относительных погрешностей отдельной варианты (ε) и среднего результата ( из выражений (2.2) и (2.4) используют при вычислении относительных погрешностей отдельной варианты (ε) и среднего результата (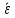 ), выражая эти величины в %: ), выражая эти величины в %: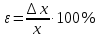 , (2.7) , (2.7)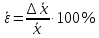 . (2.8) . (2.8)Пример 2.1. В результате определения содержания хинона в стандартном образце хингидрона были получены следующие данные (n = 10):
Расчеты по формулам (1.2), (1.4), (1.5), (1.6), (1.9) дали следующие результаты:  = 49,96; f = 9; s2 = 0,01366; s = 0,1169; s = 49,96; f = 9; s2 = 0,01366; s = 0,1169; s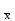 = 0,03696. = 0,03696.Доверительные интервалы результата отдельного определения и среднего результата при Р = 90 % получаем согласно (2.4) и (2.2): 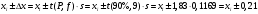 ; ;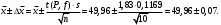 Тогда относительные погрешности 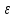 и и 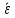 , согласно (2.7) и (2.8), равны: , согласно (2.7) и (2.8), равны: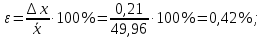 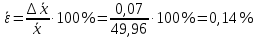 . .Обозначая истинное содержание хинона в хингидроне через µ, можно считать, что с 90 % доверительной вероятностью справедливы неравенства: 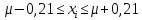 ; ;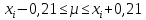 (при любом i); (при любом i);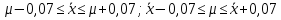 (при n = 10). (при n = 10).Примечание 2.2. Вычисление доверительных интервалов для случая, описанного в примечании 1.2, проводят, исходя из логарифмов вариант. Тогда выражения (2.2) и (2.4) принимают вид: lg 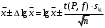 ; (2.9) ; (2.9)lg 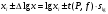 .(2.10) .(2.10)Потенцирование выражений (2.9) и (2.10) приводит к несимметричным доверительным интервалам для значений х и xi. antilg(lg  – – 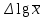 ) ) 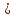  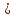 antilg(lg antilg(lg + + 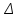 lg lg ); (2.11) ); (2.11)antilg(lgxi – 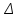 lgxi) lgxi) 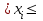 antilg(lgxi + antilg(lgxi + 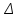 lgxi), (2.12) lgxi), (2.12)где 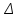 lg lg = = 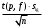 ; ;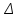 lg xi = lg xi = 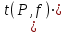 slg. slg.При этом для нижних и верхних границ доверительных интервалов  и x имеем: и x имеем: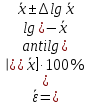 ; (2.12 a) ; (2.12 a)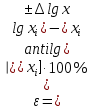 . (2.12 б) . (2.12 б)3. Метрологическая характеристика метода анализа. Сравнение двух методов анализа по воспроизводимости. С целью получения метрологической характеристики метода проводят совместную статистическую обработку одной или нескольких выборок, полученных при анализе образцов с известным содержанием определяемого компонента µ. Результаты статистической обработки представляют в виде табл. 1. Таблица 1 Метрологические характеристики метода анализа
*- Графа 10 заполняется в том случае, если реализуется неравенство (3.2). Примечание 3.1. При проведении совместной статистической обработки нескольких выборок, полученных при анализе образцов с разным содержанием определяемого компонента µ, данные в графах 1, 2, 3, 4, 9 и 10 табл. 1 приводят отдельно для каждой выборки. При этом в графах 2, 4, 5, 7, 8 в последней строке под чертой приводят обобщенные значения f, s2, s, t, 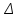 х, вычисленные с учетом примечания 1.1. х, вычисленные с учетом примечания 1.1.Если для выборки объема m величина 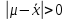 , следует решить вопрос о наличии или отсутствии систематической ошибки. Для этого вычисляют критерий Стьюдента t: , следует решить вопрос о наличии или отсутствии систематической ошибки. Для этого вычисляют критерий Стьюдента t:t = 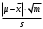 . (3.1) . (3.1)Если, например, при Р = 95 % и f = m − 1, реализуется неравенство t > t (P, f), (3.2) то полученные данным методом результаты отягощены систематической ошибкой, относительная величина которой δ вычисляется по формуле: 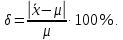 (3.3) (3.3)Следует помнить, что если величина А определена как среднее  некоей выборки, полученной эталонным методом, критерий Стьюдента t может рассчитываться по уравнению (4.5). некоей выборки, полученной эталонным методом, критерий Стьюдента t может рассчитываться по уравнению (4.5).При сравнении воспроизводимости двух методов анализа с оценками дисперсий 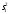 и и 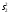 ( (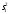 > > 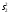 ) вычисляют критерий Фишера F: ) вычисляют критерий Фишера F:F = 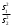 . (3.4) . (3.4)Критерий F характеризует при 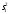 > > 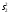 достоверность различия между достоверность различия между 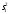 и и 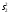 . Вычисленное значение F сравнивают с табличным значением F(P, f1, f2), найденным при P = 99 % (см. табл. III приложения). Если для вычисленного значения F выполняется неравенство: . Вычисленное значение F сравнивают с табличным значением F(P, f1, f2), найденным при P = 99 % (см. табл. III приложения). Если для вычисленного значения F выполняется неравенство:F > F (P, f1, f2), (3.5) различие дисперсий 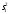 и и 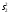 признается статистически значимым с вероятностью Р, что позволяет сделать заключение о более высокой воспроизводимости второго метода. Если выполняется неравенство: признается статистически значимым с вероятностью Р, что позволяет сделать заключение о более высокой воспроизводимости второго метода. Если выполняется неравенство:F 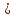 F(P, f1, f2), (3.5 а) F(P, f1, f2), (3.5 а)различие значений 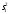 и и 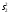 не может быть признано значимым и заключение о различии воспроизводимости методов сделать нельзя ввиду недостаточного объема информации. не может быть признано значимым и заключение о различии воспроизводимости методов сделать нельзя ввиду недостаточного объема информации.Примечание 3.2. Для случая, описанного в примечании 1.2, в табл. 1 вместо величин µ,  , , 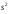 иs приводят величины lgµ, lg иs приводят величины lgµ, lg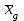 , , 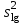 и и 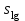 . При этом в графу 8, согласно примечанию 2.2, вносят величину . При этом в графу 8, согласно примечанию 2.2, вносят величину 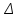 lg x, а в графу 9 – максимальное по абсолютной величине значение ε. Аналогичные замены проводят при вычислении t по уравнению (3.1) и F – по уравнению (3.4). lg x, а в графу 9 – максимальное по абсолютной величине значение ε. Аналогичные замены проводят при вычислении t по уравнению (3.1) и F – по уравнению (3.4).Для сравнения двух методов анализа результаты статистической обработки сводят в табл.2. Таблица 2 Данные для сравнительной метрологической оценки двух методов анализа
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
