1.1.13 отчет. 1.1.13._(ОФС.1.1.0013.15). Статья статистическая обработка результатов офс 0013. 15
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
Таблица 6 Значения аргумента х и функции у.
Тогда: 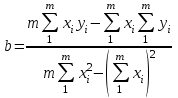 , (6.4) , (6.4)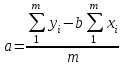 , (6.5) , (6.5)f = m – 2. (6.6) Если полученные значения коэффициентов а и b использовать для вычисления значений у по заданным в табл. 6 значениям аргумента х согласно зависимости (6.1), то вычисленные значения у обозначают через Y1, Y2, ... , Yi, ... Yn. Разброс значений Yi относительно значений уi характеризуется величиной дисперсии s 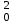 , которую вычисляют по уравнению: , которую вычисляют по уравнению: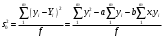 . (6.7) . (6.7)В свою очередь, дисперсии констант b и а находят по уравнениям: s 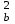 = = 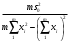 ; (6.8) ; (6.8)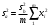 . (6.9) . (6.9)Стандартные отклонения sb и sa и величины 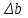 и и 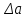 , необходимые для оценки доверительных интервалов констант уравнения регрессии, рассчитывают по уравнениям: , необходимые для оценки доверительных интервалов констант уравнения регрессии, рассчитывают по уравнениям: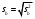 ; (6.10) ; (6.10)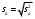 ; (6.11) ; (6.11)∆b = t(P,f)∙sb; (6.12) ∆a = t(P,f)∙sa. (6.13) Уравнению (6.1) с константами а и b обязательно удовлетворяет точка с координатами  и и 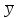 , называемая центром калибровочного графика: , называемая центром калибровочного графика: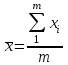 ; (6.14) ; (6.14)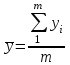 . (6.15) . (6.15)Наименьшие отклонения значений yi от значений Yi наблюдаются в окрестностях центра графика. Стандартные отклонения sy и sx величин Y и X, рассчитанных соответственно по уравнениям (6.1) и (6.2), исходя соответственно из известных значений х и у, определяются с учетом удаления последних от центра графика: 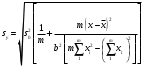 ; (6.16) ; (6.16)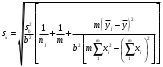 , (6.17) , (6.17)где 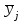 – среднее значение дляnj вариант y, по которым вычислено – среднее значение дляnj вариант y, по которым вычислено искомое значение X. При x =  и и 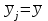 выражения (6.16) и (6.17) принимают вид: выражения (6.16) и (6.17) принимают вид: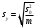 ; (6.16 а) ; (6.16 а)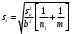 . (6.17 а) . (6.17 а)С учетом значений sy и sx могут быть найдены значения величин ∆Y и ∆X: ∆Y = sy∙t(P, f); (6.18) ∆X = sx∙t(P, f). (6.19) Значения sx и ∆X, найденные при nj = 1, являются характеристиками воспроизводимости аналитического метода, если х – концентрация (количество), а у есть функция х. Обычно результаты статистической обработки по методу наименьших квадратов сводят в таблицу (табл. 7). Таблица 7 Результаты статистической обработки экспериментальных данных, полученных при изучении линейной зависимости у = bx + a
Примечание 6.1. Если целью экспериментальной работы являлось определение констант b и a, графы 11, 12 и 13 табл. 7 не заполняются. П 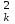 римечание 6.2. Если y = b∙lg x + a, вычисления, описанные в разделе 6, выполняют с учетом примечаний 1.2 и 2.2. Примечание 6.3. Сравнение дисперсий 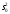 , полученных в разных условиях для двух линейных зависимостей, может быть проведено, как указано в разделе 3 (см. выражения (3.4), (3.5) и (3.5 а)). , полученных в разных условиях для двух линейных зависимостей, может быть проведено, как указано в разделе 3 (см. выражения (3.4), (3.5) и (3.5 а)).7. Расчет неопределенности функции нескольких случайных переменных Описанные в разделах 1 – 6 настоящей общей фармакопейной статьи расчеты доверительных интервалов результатов методик анализа применимы лишь в том случае, если измеряемая величина (концентрация, содержание и т.д.) является функцией только одной случайной переменной. Такая ситуация обычно возникает при использовании прямых методов анализа (титрование, определение сульфатной золы, тяжелых металлов и т.д.). Однако большинство методик количественного определения в фармакопейном анализе являются косвенными, то есть используют стандартные образцы. Следовательно, измеряемая величина является функцией, как минимум, двух случайных переменных – аналитических сигналов (оптическая плотность, высота или площадь пика и т.д.) испытуемого и стандартного образцов. Кроме того, нередко возникает проблема прогнозирования неопределенности аналитической методики, состоящей из нескольких стадий (взвешивание, разбавление, конечная аналитическая операция), каждая из которых является по отношению к другой случайной величиной. Таким образом, возникает общая проблема оценки неопределенности косвенно измеряемой величины, зависящей от нескольких измеряемых величин, в частности, как рассчитывать неопределенность всей аналитической методики, если известны неопределенности отдельных ее составляющих (стадий)? Если измеряемая на опыте величина у является функцией п независимых случайных величин хi, то есть: (7.1) и число степеней свободы величин xiодинаково или достаточно велико (> 30, чтобы можно было применять статистику Гаусса, а не Стьюдента), то дисперсия величины у связана с дисперсиями величин xiсоотношением (правило распространения неопределенностей): 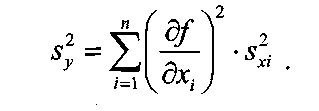 (7.2) (7.2)Однако на практике степени свободы величин xtобычно невелики и не равны друг другу. Кроме того, обычно интерес представляют не сами дисперсии (стандартные отклонения), а доверительные интервалы, рассчитать которые, используя уравнение (7.2), при небольших и неодинаковых степенях свободы невозможно. Поэтому для расчета неопределенности величины у (Δу) предложены различные подходы, среди которых можно выделить два основных: линейная модель и подход Уэлча–Сатертуэйта. 7.1. Линейная модель Если случайные переменные хiстатистически независимы, то доверительный интервал функции Δусвязан с доверительными интервалами переменных Δxiсоотношением (доверительные интервалы берутся для одной и той же вероятности): 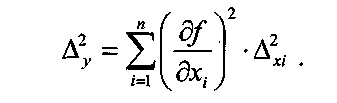 (7.3) (7.3)Данное выражение является обобщением соотношения (7.2). В фармакопейном анализе измеряемая величина у представляет собой обычно произведение или частное случайных и постоянных величин (масс навесок, разбавлений, оптических плотностей или площадей пиков и т.д.), т.е. (К - некая константа): 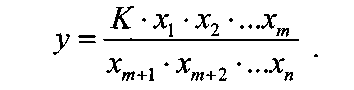 (7.4) (7.4) В этом случае соотношение (7.2) принимает вид: 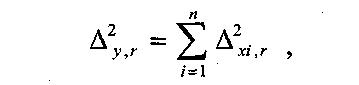 (7.5) (7.5)где использованы относительные доверительные интервалы. Соотношение (7.4) применимо при любых (разных) степенях свободы (в том числе и бесконечных) для величин xi. Его преимуществом является простота и наглядность. Использование абсолютных доверительных интервалов приводит к гораздо более громоздким выражениям, поэтому рекомендуется использовать относительные величины. При проведении фармакопейного анализа в суммарной неопределенности (ΔAS:r) анализа обычно всегда можно выделить такие типы неопределенностей: неопределенность пробоподготовки (ΔSPr), неопределенность конечной аналитической операции (ΔFAO,r) и неопределенность аттестации стандартного образца (ΔRS,r). Величина ΔRS,r обычно столь мала, что ею можно пренебречь. Учитывая это, а также то, что анализ проводится и для испытуемого раствора (индекс "smp"), и для раствора сравнения (индекс "st"), выражение (7.5) можно представить в виде: При этом каждое из слагаемых рассчитывается из входящих в него компонентов по формуле (7.5). Если число степеней свободы величин хiодинаково или достаточно велико (> 30), выражение (7.5) дает: 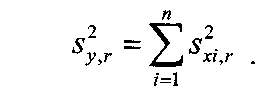 (7.7) (7.7)Это же соотношение получается при тех же условиях и из выражения (7.2). 7.2. Подход Уэлча–Сатертуэйта В этом подходе дисперсию величины у (s2у) рассчитывают по соотношению (7.2), не обращая внимания на различие в степенях свободы (νi) величин xi. Для полученной дисперсии s2у рассчитывают некое «эффективное» число степеней свободы veff(которое обычно является дробным), на основе которого затем по таблицам для заданной вероятности находят интерполяцией значения критерия Стьюдента. На основе его далее рассчитывают обычным путем доверительный интервал величины у (Δу): 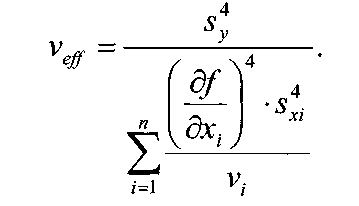 (7.8) (7.8)В фармакопейном анализе для определяемой величины у обычно выполняется уравнение (7.4). В этом случае в подходе Уэлча–Сатертуэйта соотношение (7.2) переходит в выражение (7.7), и соотношение (7.8) принимает более простой вид: 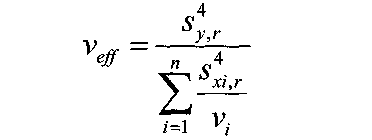 (7.9) (7.9)Здесь величина sy,r4 рассчитывается из соотношения (7.7). Подход Уэлча–Сатертуэйта обычно дает более узкие доверительные интервалы, чем линейная модель. Однако он гораздо сложнее в применении и не позволяет выделить так просто неопределенности разных этапов (с последующими рекомендациями по их минимизации), как линейная модель в форме выражения (7.6). При прогнозе неопределенности анализа используются генеральные величины (с бесконечным числом степеней свободы). В этом случае подход Уэлча–Сатертуэйта совпадает с линейной моделью. |