ОФС_Статистическая_обработка_результатов_физических__физико-хими. Статья статистическая обработка результатов физических, физикохимических и химических испытаний
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
1.4. Объединение однородных выборок 1.4.1.Объединенная дисперсия и объединенное среднее значение Если имеется g выборок из одной и той же генеральной совокупности с порядковыми номерами k (1 ≤ k ≤ g), расчет объединенной дисперсии 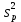 проводят по формуле: проводят по формуле: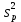 = = 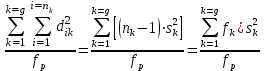 (1.14) (1.14)или для объединенных относительных величин: 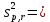 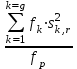 (1.14а) (1.14а) 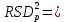 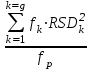 (1.14б) (1.14б)При этом объединенное число степеней свободы 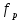 равно: равно: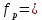 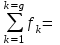 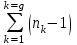 (1.15), где: (1.15), где: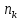 – число вариант в k-той выборке; – число вариант в k-той выборке;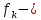 число степеней свободы в k-той выборке; число степеней свободы в k-той выборке;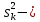 дисперсия k-той выборки; дисперсия k-той выборки;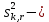 относительная дисперсия k-той выборки; относительная дисперсия k-той выборки;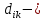 отклонение i-той варианты вk-той выборке. отклонение i-той варианты вk-той выборке.Если g выборок из одной и той же генеральной совокупности с порядковыми номерами k (1 ≤ k ≤ g) характеризуются выборочными средними значениями 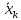 , полученными из , полученными из 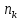 вариант, объединенное среднее значение вариант, объединенное среднее значение 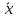 по всем выборкам рассчитывают по формуле: по всем выборкам рассчитывают по формуле: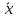 = = 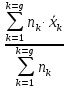 (1.16) (1.16)Необходимым условием совместной статистической обработки нескольких однородных выборок является отсутствие статистически значимой разницы между отдельными значениями 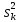 в уравнении (1.14), в уравнении (1.14), 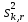 в уравнении (1.14а) или в уравнении (1.14а) или 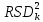 в уравнении (1.14б), т. е. справедливость гипотезы равенства дисперсий. В простейшем случае можно ограничиться сравнением крайних значений в уравнении (1.14б), т. е. справедливость гипотезы равенства дисперсий. В простейшем случае можно ограничиться сравнением крайних значений 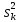 с использованием критерия Фишера F. В более общем случае можно использовать критерии Бартлетта и Кохрена. с использованием критерия Фишера F. В более общем случае можно использовать критерии Бартлетта и Кохрена.1.4.2. Критерий Бартлетта Для проверки гипотезы, что все 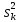 принадлежат к одной генеральной совокупности, используют выражение, приближенно распределенное как принадлежат к одной генеральной совокупности, используют выражение, приближенно распределенное как 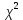 : :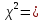 2,303·(fp ·lg s- 2,303·(fp ·lg s-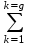 fklgs2k) (1.17) fklgs2k) (1.17)При этом величины s2и 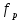 рассчитывают по уравнениям (1.14) и (1.15). Найденную таким образом величину рассчитывают по уравнениям (1.14) и (1.15). Найденную таким образом величину 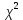 сравнивают с процентной точкой хи-квадрат распределения сравнивают с процентной точкой хи-квадрат распределения 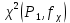 (таблица 7.5. Приложения ). Если имеется g выборок, то число степеней свободы для (таблица 7.5. Приложения ). Если имеется g выборок, то число степеней свободы для 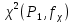 берут равным берут равным 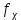 = g – 1. Проверяемую гипотезу принимают при условии = g – 1. Проверяемую гипотезу принимают при условии 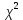 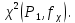 В противном случае вычисленное значение В противном случае вычисленное значение 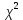 корректируют по формуле: корректируют по формуле: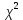 = =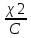 (1.18) (1.18)где : С= 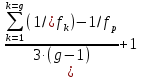 , (1.19) , (1.19)и снова сравнивают с процентной точкой хи-квадрат распределения 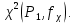 Если Если 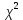 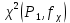 , томежду некоторыми стандартными отклонениями имеются значимые различия.В этом случае необходимо провести анализ имеющихся данных, отбросить одно или несколько значений дисперсии, наиболее сильно отличающихся от остальных, и снова провести тест Бартлетта. Необходимо иметь в виду, что критерий Бартлетта, так же, как критерий Кохрена, очень чувствителен к нарушению требования нормального распределения. Но именно поэтому он может быть весьма полезен при сборе и формировании надежного архива данных о тех или иных аналитических испытаниях. , томежду некоторыми стандартными отклонениями имеются значимые различия.В этом случае необходимо провести анализ имеющихся данных, отбросить одно или несколько значений дисперсии, наиболее сильно отличающихся от остальных, и снова провести тест Бартлетта. Необходимо иметь в виду, что критерий Бартлетта, так же, как критерий Кохрена, очень чувствителен к нарушению требования нормального распределения. Но именно поэтому он может быть весьма полезен при сборе и формировании надежного архива данных о тех или иных аналитических испытаниях.Описанный критерий Бартлетта применим только при условии, что число степеней свободы у всех объединяемых дисперсий больше 3, т.е. все 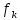 3. 3. 1.4.3. Критерий Кохрена В том случае, когда все объединяемые дисперсии имеют одинаковое число степеней свободы (т.е. f1 = f2 = …= fg = f) для проверки гипотезы равенства дисперсий (однородности дисперсий) можно применять значительно более простой критерий Кохрена со статистикой: G = 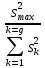 (1.20) (1.20) где: 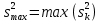 . .В формулах (1.17) и (1.20) вместо абсолютных величин 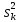 могут быть использованы относительные величины могут быть использованы относительные величины 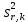 и RSDk. и RSDk.Критические точки критерия Кохрена приведены в таблице 7.6. Приложения. Для подтверждения гипотезы об однородности дисперсий рассчитанное значение Gна выбранном уровне значимости (95 % или 99 %) не должно превосходить табличное значение (Gрассчитанное ≤ Gтабличное. В противном случае гипотеза равенства дисперсий не может быть принята: формулы (1.15) - (1.17) объединения выборок не являются корректными, наибольшую дисперсию в исследуемом наборе дисперсий считают выболсом.. 1.5. Доверительные интервалы и оценка их величины Если случайная однородная выборка конечного объема n получена в результате последовательных измерений некоторой величины А, имеющей истинное значение µ, то среднее этой выборки  следует рассматривать лишь как приближенную оценку величины А. Достоверность этой оценки характеризуется величиной доверительного интервала следует рассматривать лишь как приближенную оценку величины А. Достоверность этой оценки характеризуется величиной доверительного интервала 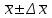 , для которой с заданной доверительной вероятностью Р выполняется условие: , для которой с заданной доверительной вероятностью Р выполняется условие: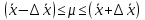 (1.21) (1.21)Данный доверительный интервал не характеризует погрешность определения величины µ, поскольку найденная величина 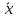 может быть в действительности очень близка к истинному значению µ, которое остается неизвестным. Полученный доверительный интервал характеризует степень неопределенности наших знаний об истинном значении µвеличины А по результатам последовательных измерений выборки конечного объема n. Поэтому правильно говорить о «неопределенности результатов анализа», которая характеризуется доверительным интервалом, вместо выражения «погрешность результатов анализа», которое нередко не совсем корректно используется. может быть в действительности очень близка к истинному значению µ, которое остается неизвестным. Полученный доверительный интервал характеризует степень неопределенности наших знаний об истинном значении µвеличины А по результатам последовательных измерений выборки конечного объема n. Поэтому правильно говорить о «неопределенности результатов анализа», которая характеризуется доверительным интервалом, вместо выражения «погрешность результатов анализа», которое нередко не совсем корректно используется.Расчет граничных значений доверительного интервала при известном значении стандартного отклонения s или для выборок большого объема проводят по уравнению: 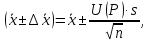 (1.22а) (1.22а)предполагая, что варианты, входящие в выборку, распределены нормально. Здесь U(P) – табличное значение функции нормального распределения. Для выборок небольшого объема расчет граничных значений доверительного интервала проводят с использованием критерия Стьюдента, предполагая, что варианты, входящие в выборку, распределены нормально: 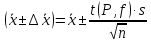 (1.22б) (1.22б)или с использованием относительных величин: 1 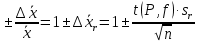 (1.22в) (1.22в)Здесь t (P, f) – табличное значение критерия Стьюдента (таблица 7.2. Приложения). Распределение по критерию Стьюдента 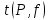 является обобщением нормального распределенияU(P) и переходит в него при достаточно большом числе степеней свободы является обобщением нормального распределенияU(P) и переходит в него при достаточно большом числе степеней свободы 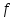 , т.е. , т.е.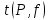 →U(P). С учетом этого далее для единообразия везде используется более часто употребляемые соотношения (1.22б) и (1.22в), даже в случае выборок достаточно большого объема. →U(P). С учетом этого далее для единообразия везде используется более часто употребляемые соотношения (1.22б) и (1.22в), даже в случае выборок достаточно большого объема.Полуширины относительных доверительных интервалов единичного ( 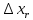 ) и среднего ( ) и среднего (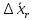 ) результатов часто выражают в процентах по отношению к ) результатов часто выражают в процентах по отношению к 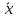 . В этом случае в выражении (1.22в) вместо величины . В этом случае в выражении (1.22в) вместо величины 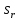 используют RSD, а вместо 1 указывают 100 %, т.е.: используют RSD, а вместо 1 указывают 100 %, т.е.: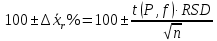 (1.22г) (1.22г)Если при измерении одной и той же методикой двух близких значений А были получены две случайные однородные выборки с объемами n и m, то при m < n для выборки объема m справедливо уравнение: 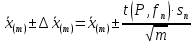 , (1.23) , (1.23)где индекс указывает принадлежность величин к выборке объема mили n. Уравнение (1.23) позволяет оценить величину доверительного интервала среднего 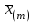 , найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего , найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего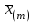 для выборки относительно малого объема m может быть сужен благодаря использованию известных величин s(n) и t(P, fn), найденных ранее для выборки большего объема n. Более общим подходом является объединение выборок с расчетом объединенного стандартного отклонения и степеней свободы по уравнениям (1.14)-(1.15). Это стандартное отклонение и соответствующий объединенному числу степеней свободы критерий Стьюдента подставляют затем в выражение (1.22г). для выборки относительно малого объема m может быть сужен благодаря использованию известных величин s(n) и t(P, fn), найденных ранее для выборки большего объема n. Более общим подходом является объединение выборок с расчетом объединенного стандартного отклонения и степеней свободы по уравнениям (1.14)-(1.15). Это стандартное отклонение и соответствующий объединенному числу степеней свободы критерий Стьюдента подставляют затем в выражение (1.22г).Аналогично уравнениям (1.21)-(1.22) определяют доверительный интервал результата отдельного определения. Подставляя n= 1 в уравнение (1.22б) или m = 1 в уравнение (1.23), получают: 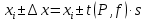 (1.24) (1.24)или с использованием относительных величин: 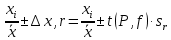 (1.24а) (1.24а)Этот интервал является доверительным интервалом результата отдельного определения. Для него с доверительной вероятностью Р выполняются взаимосвязанные условия: 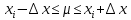 (1.25) (1.25)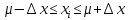 (1.26) (1.26)Значения 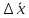 и и 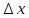 из уравнений (1.22б) и (1.24) используют при вычислении относительных неопределенностей отдельной варианты (ε) и среднего результата ( из уравнений (1.22б) и (1.24) используют при вычислении относительных неопределенностей отдельной варианты (ε) и среднего результата (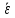 ), выражая эти величины в процентах: ), выражая эти величины в процентах: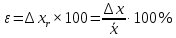 (1.27) (1.27)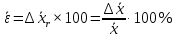 (1.28) (1.28)Пример расчета доверительных интервалов в процентах и относительных неопределенностей приведен в разделе 6.3. Если при измерениях получают логарифмы исходных вариант, то уравнения (1.22б) и (1.24) принимают вид: lg 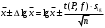 ; (1.29) ; (1.29)lg 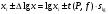 (1.30) (1.30)Потенцирование выражений (1.29) и (1.30) приводит к несимметричным доверительным интервалам для значений 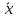 и и 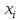 : :antilg(lg  – – 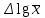 ) ) 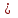  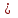 antilg(lg antilg(lg + + 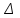 lg lg ); (1.31) ); (1.31)antilg(lgxi – 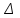 lgxi) lgxi) 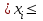 antilg(lgxi + antilg(lgxi + 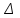 lgxi), (1.32) lgxi), (1.32)где: 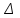 lg lg = = 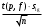 ; (1.33) ; (1.33)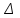 lg xi = lg xi = 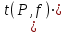 slg. (1.34) slg. (1.34)При этом для нижних и верхних границ доверительных интервалов  и x относительные неопределенности составляют: и x относительные неопределенности составляют: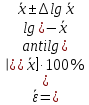 ; (1.35а) ; (1.35а)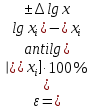 . (1.35б). . (1.35б).1.5.1. Односторонние и двусторонние доверительные интервалы Выражения (1.21) - (1.35) характеризуют так называемые «двусторонние» доверительные интервалы. Они основаны на двустороннем t-распределении и широко применяются при оценке правильности и прецизионности методик и представлении результатов. Вместе с тем, при решении некоторых задач, например, при контроле готовой продукции, в частности, при контроле качества лекарственных средств, нередко возникает необходимость использования так называемых «односторонних» доверительных интервалов. Например, для какого-нибудь лекарственного препарата допуски количественного содержания действующего вещества установлены от 90 % до 110 % от номинального. В процессе анализа получено среднее значение содержания  = 94 % от номинального значения. Необходимо решить, не выходит ли доверительный интервал за допуски содержания (90-110 %). Очевидно, что в данном случае этот доверительный интервал может выйти за пределы только нижнего допуска (90 %), но не верхнего (110 %) одновременно. Вопрос о возможности выхода истинной величины µ за пределы верхнего допуска не рассматривают, в связи с его крайне низкой вероятностью. Таким образом, истинное значение µ находится в интервале: = 94 % от номинального значения. Необходимо решить, не выходит ли доверительный интервал за допуски содержания (90-110 %). Очевидно, что в данном случае этот доверительный интервал может выйти за пределы только нижнего допуска (90 %), но не верхнего (110 %) одновременно. Вопрос о возможности выхода истинной величины µ за пределы верхнего допуска не рассматривают, в связи с его крайне низкой вероятностью. Таким образом, истинное значение µ находится в интервале: 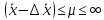 (1.36а) (1.36а)Аналогичное выражение можно записать для случая, когда  превышает 100 % (например, превышает 100 % (например,  = 105 %): = 105 %):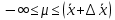 (1.36б) (1.36б)Выражения (1.36а) и (1.36б) характеризуют односторонние доверительные интервалы, поскольку величина µ ими ограничивается только с одной стороны. Это отличает их от выражения (1.21), где величина µ ограничивается с обеих сторон. Существует следующее соотношение между двусторонним (Р2) и односторонним (Р1) критериями Стьюдента: t[P2, f] =t[(2P1-1) f] (1.37) В частности, односторонний критерий Стьюдента для вероятности 0,95 (т.е. 95 %) совпадает с двусторонним критерием Стьюдента для вероятности 0,90 (т.е. 90 %). Таким образом, Р2 ‒ это вероятность того, что математическое ожидание (или истинное значение) оцениваемой величины находится в двусторонне ограниченных пределах (1.21) - (1.35), а Р1 ‒ это вероятность того, что оно находится в односторонне ограниченных пределах (1.36) - (1.35). Также могут использоваться величины, обозначаемые (1-P2) и (1-P1), которые характеризуют вероятность того, что математическое ожидание (или истинное значение) оцениваемой величины выходит за вышеуказанные пределы. Во многих случаях такие величины являются более удобными. |
