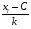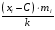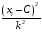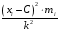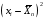Расчетно-графическая работа
Исходные данные
1. Генеральная совокупность с нормальным распределением; среднее значение А = 16; дисперсия Т2 = 16.
2. Предельные ошибки выборки 0,65.
Уровни значимости α1 = 0,03; 0,02; 0,05; К= 0.
Выборка 1
15,93
|
15,17
|
15,88
|
18,80
|
17,77
|
12,12
|
13,82
|
19,02
|
15,62
|
21,11
|
14,23
|
13,66
|
12,15
|
21,05
|
15,02
|
10,82
|
10,86
|
21,71
|
16,69
|
17,91
|
17,50
|
20,82
|
18,70
|
16,85
|
13,82
|
16,44
|
15,34
|
18,71
|
12,78
|
16,44
|
9,27
|
12,18
|
18,91
|
16,02
|
14,31
|
15,51
|
11,61
|
18,85
|
19,79
|
13,77
|
15,84
|
10,24
|
17,17
|
20,19
|
14,90
|
19,71
|
20,68
|
19,96
|
19,15
|
17,29
|
Для заданной статистической совокупности:
составить интервальный вариационный ряд;
вычислить относительные частоты;
вычислить эмпирическую функцию распределения;
построить графики (гистограммы) относительных частот и эмпирической функции распределения;
вычислить выборочные: среднее значение, дисперсию, среднеквадратическое отклонение и определить выборочные моду и медиану.
Для построения интервального ряда необходимо упорядочить выборку, т.е. построить вариационный ряд.
9,27
|
10,24
|
10,82
|
10,86
|
11,61
|
12,12
|
12,15
|
12,18
|
12,78
|
13,66
|
13,77
|
13,82
|
13,82
|
14,23
|
14,31
|
14,9
|
15,02
|
15,17
|
15,34
|
15,51
|
15,62
|
15,84
|
15,88
|
15,93
|
16,02
|
16,44
|
16,44
|
16,69
|
16,85
|
17,17
|
17,29
|
17,5
|
17,77
|
17,91
|
18,7
|
18,71
|
18,8
|
18,85
|
18,91
|
19,02
|
19,15
|
19,71
|
19,79
|
19,96
|
20,19
|
20,68
|
20,82
|
21,05
|
21,11
|
21,71
|
Объем выборки N = 50; Xmin = 9,27; Xmax = 21,71.
Размах вариации R = Xmax – Xmin = 12,44;
Количество интервалов n = 7
Ширина интервала равна 1,78; k = 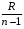 = 2,073; С = 15,49 (соответствует середине интервала хi для максимальной частоты mi). = 2,073; С = 15,49 (соответствует середине интервала хi для максимальной частоты mi).
Эмпирическая функция распределения находится как накопленная частота
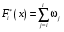
Интервал
|
хi
|
mi
|
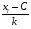
|
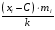
|
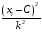
|
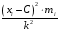
|
ωi

|
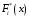
|
[9,27; 11,05)
|
10,16
|
4
|
-3
|
-12
|
9
|
36
|
0,08
|
0,08э
|
[11,05; 12,82)
|
11,94
|
5
|
-2
|
-10
|
4
|
20
|
0,1
|
0,18
|
[12,82; 14,60)
|
13,71
|
6
|
-1
|
-6
|
1
|
6
|
0,12
|
0,3
|
[14,60; 16,38)
|
15,49
|
10
|
0
|
0
|
0
|
0
|
0,2
|
0,5
|
[16,38; 18,16)
|
17,27
|
9
|
1
|
9
|
1
|
9
|
0,18
|
0,68
|
[18,16; 19,93)
|
19,04
|
9
|
2
|
18
|
4
|
36
|
0,18
|
0,86
|
[19,93; 21,71)
|
20,82
|
7
|
3
|
21
|
9
|
63
|
0,14
|
1
|
|
|
50
|
|
28
|
|
170
|
1
|
|
Гистограмма относительных частот для интервального ряда
График эмпирической функции распределения
Определяем выборочное среднее значение, дисперсию, среднеквадратическое отклонение, моду и медиану для интервального вариационного ряда
Среднее значение: 
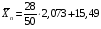 = 16,65 = 16,65
Дисперсия: 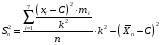 ; ;
 = 13,27 = 13,27
Среднеквадратическое отклонение (исправленное): 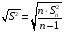
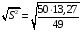 = 3,68 = 3,68
Мода – значение признака, встречающегося чаще всего в вариационном ряду. Для интервального ряда мода определяется по наибольшей частоте. Мода находится по формуле:
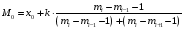 , ,
где x0 – нижняя (начальная) граница модального интервала;
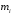 – частота модального интервала – частота модального интервала
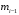 – частота интервала, предшествующего модальному; – частота интервала, предшествующего модальному;
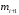 – частота интервала, следующего за модальным. – частота интервала, следующего за модальным.
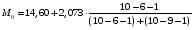 = 16,67 = 16,67
Медиана – значение признака, разделяющего совокупность на две равные части, т.е. 50% единиц выборки имеют значение меньше медианы, а другие – больше медианы.
Медиана: 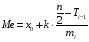 . .
Здесь x0 – нижняя (начальная) граница медианного интервала;
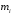 – частота медианного интервала; – частота медианного интервала;
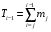 – частота, накопленная до медианного интервала. – частота, накопленная до медианного интервала.
 = 16,67 = 16,67
2. Используя выборки 2 и 3, по дискретному вариационному ряду вычислить несмещенные оценки для среднего значения, дисперсии, среднеквадратического отклонения генеральной совокупности.
Выборка 2
9,27
|
10,24
|
10,82
|
10,86
|
11,61
|
13,77
|
13,82
|
13,82
|
14,23
|
14,31
|
15,62
|
15,84
|
15,88
|
15,93
|
16,02
|
17,29
|
17,5
|
17,77
|
17,91
|
18,7
|
19,15
|
19,71
|
19,79
|
19,96
|
20,19
|
Выборка 3
12,12
|
12,15
|
12,18
|
12,78
|
13,66
|
14,9
|
15,02
|
15,17
|
15,34
|
15,51
|
16,44
|
16,44
|
16,69
|
16,85
|
17,17
|
18,71
|
18,8
|
18,85
|
18,91
|
19,02
|
20,68
|
20,82
|
21,05
|
21,11
|
21,71
|
Оценка среднего значения: 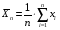 . .
Оценка дисперсии и среднекапдратического отклонения

Промежуточные вычисления записываем в таблицу.
№ п/п
|
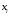
|

|
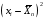
|
1
|
9,27
|
-6,33
|
40,07
|
2
|
13,77
|
-1,83
|
3,35
|
3
|
15,62
|
0,02
|
0,00
|
4
|
17,29
|
1,69
|
2,85
|
5
|
19,15
|
3,55
|
12,60
|
6
|
10,24
|
-5,36
|
28,73
|
7
|
13,82
|
-1,78
|
3,17
|
8
|
15,84
|
0,24
|
0,06
|
9
|
17,50
|
1,90
|
3,61
|
10
|
19,71
|
4,11
|
16,89
|
11
|
10,82
|
-4,78
|
22,85
|
12
|
13,82
|
-1,78
|
3,17
|
13
|
15,88
|
0,28
|
0,08
|
14
|
17,77
|
2,17
|
4,71
|
15
|
19,79
|
4,19
|
17,55
|
16
|
10,86
|
-4,74
|
22,47
|
17
|
14,23
|
-1,37
|
1,88
|
18
|
15,93
|
0,33
|
0,11
|
19
|
17,91
|
2,31
|
5,33
|
20
|
19,96
|
4,36
|
19,01
|
21
|
11,61
|
-3,99
|
15,92
|
22
|
14,31
|
-1,29
|
1,67
|
23
|
16,02
|
0,42
|
0,18
|
24
|
18,70
|
3,10
|
9,61
|
25
|
20,19
|
4,59
|
21,06
|
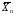
|
15,60
|
S2
|
10,71
|
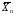 = 15,60; S2 = 10,71; S = 3,27 = 15,60; S2 = 10,71; S = 3,27
№ п/п
|
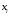
|

|
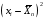
|
1
|
12,12
|
-3,48
|
12,11
|
2
|
14,9
|
-0,70
|
0,49
|
3
|
16,44
|
0,84
|
0,70
|
4
|
18,71
|
3,11
|
9,67
|
5
|
20,68
|
5,08
|
25,80
|
6
|
12,15
|
-3,45
|
11,91
|
7
|
15,02
|
-0,58
|
0,34
|
8
|
16,44
|
0,84
|
0,70
|
9
|
18,8
|
3,20
|
10,24
|
10
|
20,82
|
5,22
|
27,24
|
11
|
12,18
|
-3,42
|
11,70
|
12
|
15,17
|
-0,43
|
0,19
|
13
|
16,69
|
1,09
|
1,19
|
14
|
18,85
|
3,25
|
10,56
|
15
|
21,05
|
5,45
|
29,70
|
16
|
12,78
|
-2,82
|
7,95
|
17
|
15,34
|
-0,26
|
0,07
|
18
|
16,85
|
1,25
|
1,56
|
19
|
18,91
|
3,31
|
10,95
|
20
|
21,11
|
5,51
|
30,36
|
21
|
13,66
|
-1,94
|
3,77
|
22
|
15,51
|
-0,09
|
0,01
|
23
|
17,17
|
1,57
|
2,46
|
24
|
19,02
|
3,42
|
11,69
|
25
|
21,71
|
6,11
|
37,33
|
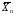
|
16,88
|
S2
|
10,78
| |
 Скачать 329.31 Kb.
Скачать 329.31 Kb.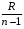 = 2,073; С = 15,49 (соответствует середине интервала хi для максимальной частоты mi).
= 2,073; С = 15,49 (соответствует середине интервала хi для максимальной частоты mi).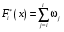

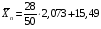 = 16,65
= 16,65 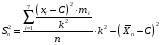 ;
; = 13,27
= 13,27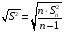
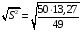 = 3,68
= 3,68 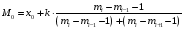 ,
,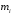 – частота модального интервала
– частота модального интервала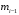 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;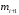 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.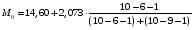 = 16,67
= 16,67 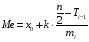 .
.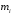 – частота медианного интервала;
– частота медианного интервала;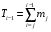 – частота, накопленная до медианного интервала.
– частота, накопленная до медианного интервала. = 16,67
= 16,67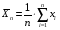 .
.
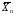 = 15,60; S2 = 10,71; S = 3,27
= 15,60; S2 = 10,71; S = 3,27