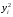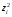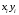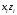Расчетно-графическая работа. Расчетнографическая работа Исходные данные
 Скачать 329.31 Kb. Скачать 329.31 Kb.
|
|
Следовательно, имеем 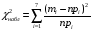 = . = .Находим число степеней свободы, учитывая, что число групп выборки 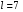 , s = 2 (число параметров теоретического распределения): , s = 2 (число параметров теоретического распределения): 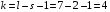 . .В таблице распределения 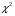 , при уровне значимости , при уровне значимости 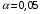 и числе степеней свободы и числе степеней свободы 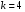 находим находим 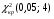 = 14,067. = 14,067.Поскольку 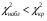 , отличие эмпирических и теоретических частот не является значимым. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности. , отличие эмпирических и теоретических частот не является значимым. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.11. С помощью метода крайних точек (натянутой нити) найти линейные функции регрессии для связанных выборок XY, XZ,YZ и построить из графики.
Корреляционная матрица
Корреляционная матрица свидетельствует о слабой связи указанных выборок. Уравнение прямой проходящей на плоскости через две точки с координатами (х 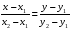 а) Крайними точками для выборок XY будут (9,27; 20,19) и (20,82; 14,31). 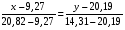 ; у = 24,91 – 0,51х. ; у = 24,91 – 0,51х.б) Крайними точками для выборок XZ будут (9,27; 19,02) и (20,82; 19,96). 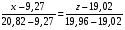 ; z = 18,26 + 0,08х. ; z = 18,26 + 0,08х.в) Крайними точками для выборок YZ будут (10,82; 12,78) и (21,05; 15,34). 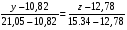 ; z = 10,07 + 0,25 у. ; z = 10,07 + 0,25 у.12. По методу наименьших квадратов найти линейные функции регрессии для двумерных выборок задачи 11 и наложить их на графики предыдущей задачи. Уравнение линейной регрессии записывается как 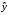 = a + bх. = a + bх.Значения коэффициентов регрессии согласно МНК вычисляются по формулам b = 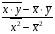 ; a = ; a = 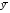 – b – b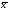 Необходимо найти математические ожидания (средние) случайных величин. Математическое ожидание случайной величины находится как 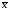 = = 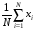 . .Здесь N – размер выборки, N = 16 а) Для выборок XY имеем 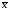 = = 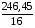 = 15,40; = 15,40; 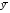 = = 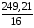 = 15,58; = 15,58;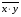 = = 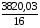 = 238,45; = 238,45; 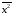 = = 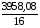 = 237,48 = 237,48b = 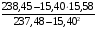 = -0,11; a = 15,58 +0,1115,40 = 17,34 = -0,11; a = 15,58 +0,1115,40 = 17,34Линейная регрессия Y на X имеет вид 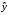 = 17,34 – 0,11х. = 17,34 – 0,11х.б) Для выборок XZ имеем 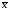 = = 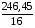 = 15,40; = 15,40; 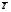 = = 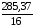 = 17.84; = 17.84;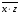 = = 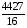 = 276.69; = 276.69; 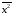 = = 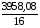 = 237,48 = 237,48b = 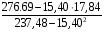 = 0,19; a = 17,84 – 0,1915,40 = 14,85 = 0,19; a = 17,84 – 0,1915,40 = 14,85Линейная регрессия Z на X имеет вид 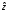 = 14,85 + 0,19х. = 14,85 + 0,19х.б) Для выборок YZ имеем 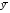 = = 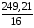 = 15,58; = 15,58; 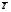 = = 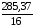 = 17.84; = 17.84;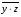 = = 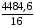 = 280,29; = 280,29; 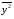 = = 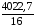 = 251,42 = 251,42b = 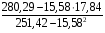 = 0,28; a = 17,84 – 0,2815,58 = 13.44 = 0,28; a = 17,84 – 0,2815,58 = 13.44Линейная регрессия Z на Y имеет вид 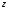 = 13.44 + 0,28y. = 13.44 + 0,28y.13. Полагая, что каждый і-й столбец в выборке 3 соответствует і-му уровню фактора А, оценить влияние фактора А на уровне значимости α10 при полностью случайном плане эксперимента. α10 = 0,05 Выборку 3 представляем как наблюдаемые значения признака.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||