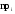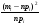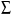Расчетно-графическая работа. Расчетнографическая работа Исходные данные
 Скачать 329.31 Kb. Скачать 329.31 Kb.
|
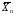 = 16,88; S2 = 10,86; S = 3,28 = 16,88; S2 = 10,86; S = 3,283. Для выборки 1, считая, что дисперсия элементов генеральной совокупности σ2 = Т2 (Т = 4):
Вероятность попадания в интервал Р = 1 – α1 = 0,97 или для нормального распределения Р = 2Ф(z). Ф(z) = 0,485; 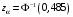 = 2,17; = 2,17;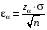 ; ; 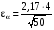 = 1,23 = 1,23Доверительный интервал 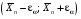 (16,65 – 1,23; 16,65 + 1,23) → (15,43; 17,88).
ε = 0,65. 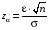 ; ; 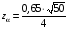 = 1,15; 0,3749; = 1,15; 0,3749; Доверительная вероятность для предельной ошибки выборки Р = 2Ф(z) = 2Ф(1,15) = 0.7498
Р = 2Ф(z) = 0,98; Ф(z) = 0,49; 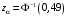 = 2,36; = 2,36;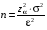 = = 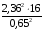 211 211Необходимый объем выборки n = 211 4. Используя выборку 2, определить доверительный интервал, соответствующий доверительной вероятности Р = α3 для оценки среднего значения генеральной совокупности. α3 = 0,05; 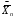 = 15,60; s = 3,27; = 15,60; s = 3,27; 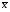 – среднее значение генеральной совокупности. – среднее значение генеральной совокупности.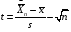 . .Для доверительной вероятности выполняется 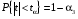 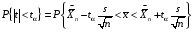 . .tαнаходим по таблице распределения Стьюдента для числа степеней свободы n – 1 = 24; tαнаходим = 2,064. 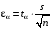 ; ; 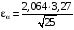 = 1,350 = 1,350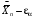 = 14,25; = 14,25; 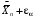 = 16,95. = 16,95.Доверительный интервал (14,25; 16,95). 5. Используя выборку 3, определить доверительный интервал, соответствующий доверительной вероятности Р = 1 – α4 для оценки дисперсии генеральной совокупности. α 4 = 0,03; Р = 0,97; S2 = 10,86. Несмещенная оценка дисперсии генеральной совокупности равна исправленной выборочной дисперсии. Рассмотрим величину случайную величину 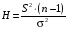 . Она имеет распределение . Она имеет распределение 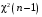 . Тогда . Тогда 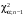 – α-квантиль распределения. Это означает, что – α-квантиль распределения. Это означает, что 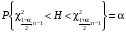 . . Откуда 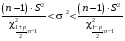 Имеем 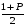 = 0,985; = 0,985; 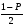 = 0,015. = 0,015.Из таблицы распределения Пирсона 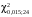 = 42,46; = 42,46; 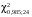 = 11,14 = 11,14Доверительный интервал для оценки генеральной дисперсии 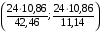 → (6,138; 23,40) → (6,138; 23,40)6. Определить доверительный интервал, соответствующий доверительной вероятности Р = 1 – α5, для доли признака. Объем выборки равен 50, выборочная доля признака равна 15. Р = 0,95 Выборочная доля 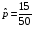 = 0,3. Предельная ошибка для доли выборки рассчитывается как = 0,3. Предельная ошибка для доли выборки рассчитывается как 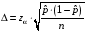 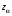 находится из условия Р = 2Ф(z). Ф(z) = 0,475; находится из условия Р = 2Ф(z). Ф(z) = 0,475;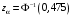 = 1,96; = 1,96;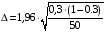 = 0,127. = 0,127.Доверительный интервал для доли признака 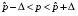 или или(0,3 – 0,127; 0,3 +0,127) → (0,173; 0,427). 7. Проверить по выборке 2 гипотезу о том, что среднее значение генеральной совокупности равно А на уровне значимости α6 при альтернативной гипотезе – среднее значение не равно А. А = 16; n = 25; 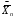 = 15,60; S = 3,27; α6 = 0,03 = 15,60; S = 3,27; α6 = 0,03Имеем гипотезы Н0: 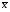 = 16. = 16.Н1: 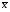 ≠ 16. ≠ 16.В качестве статистики берется величина 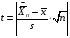 . .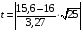 = 0,612 = 0,612По таблице распределения Стьюдента для уровня значимости 0,03 и 24 степеней свободы находим tкр = 2,349. Сравниваем полученные значения 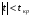 . .Следовательно, принимается гипотеза Н0: 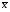 = 16. = 16.8. Проверить по выборке 3 гипотезу о том, что дисперсия генеральной совокупности равна Т2 на уровне значимости α7 при альтернативной гипотезе – дисперсия не равна Т2. n = 25; α7 = 0,05; Р = 0,95; Т2 = 16; S2 = 10,86; Имеем гипотезы Н0: σ2 = 16. Н1: σ2 ≠ 16. В качестве критерия берется величина 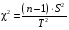 , которая имеет распределение хи-квадрат с (n – 1) степенями свободы. , которая имеет распределение хи-квадрат с (n – 1) степенями свободы.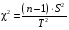 = = 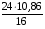 = 16,29 = 16,29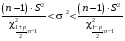 Имеем 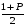 = 0,975; = 0,975; 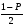 = 0,025. = 0,025.Из таблицы распределения Пирсона 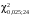 = 40,646; = 40,646; 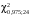 = 13,844 = 13,844Выполняется 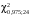 < < 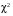 < < 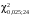 . Следовательно, принимается нулевая гипотеза. . Следовательно, принимается нулевая гипотеза.9. По выборкам 2 и 3 проверить гипотезу о том, что средние значения соответствующих генеральных совокупностей равны на уровне значимости α8 и альтернативной гипотезе – они не равны. n = 25; α8 = 0,02; Р = 0,98; 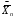 = 15,60; = 15,60; 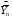 = 16,88; = 16,88;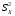 = 10,71; = 10,71; 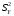 = 10,86. = 10,86.Имеем гипотезы Н0: 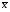 = = 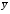 . .Н1: 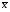 ≠ ≠ 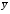 . .В качестве статистики рассматривается величина 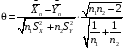 , ,имеющая распределение Стьюдента с (n1 + n2 – 2) степенями свободы. Определяется соответствующее экспериментальное значение и сравнивается с критическим tкр. 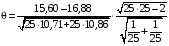 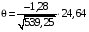 = -1,358 = -1,358 По таблице распределения Стьюдента для уровня значимости 0,02 и 48 степеней свободы находим tкр = 2,418. Сравниваем полученные значения 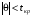 . .Следовательно, принимается нулевая гипотеза о равенстве двух генеральных средних. 10. По выборке 1 проверить гипотезу о том, что генеральная совокупность имеет нормальное распределение с параметрами 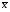 = А = 16; σ2 = Т2 = 16 на уровне значимости α9 = 0,05. = А = 16; σ2 = Т2 = 16 на уровне значимости α9 = 0,05.Имеем гипотезы Н0: {выборочная совокупность} 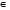 N(16; 4). N(16; 4).Н1: {выборочная совокупность} 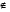 = N(16; 4). = N(16; 4).Для проверки правильности гипотезы Н0 о том, что случайная величина имеет закон распределения вероятностей N(16; 4) используем критерий согласия 2 Пирсона. Вычисление теоретических частот 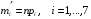 приведено в таблице: приведено в таблице:
Вычисляем наблюдаемое значение критерия 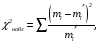 для чего составим расчетную таблицу для чего составим расчетную таблицу
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

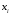
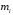
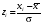
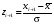
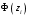
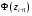
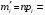
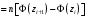
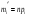
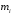 –
–