КУРСОВАЯ РАБОТА: Гармонические полиномы. Курсовая Работа.Гамзатов М.В. 3К1ГР. Курсовая работа Гармонические полиномы
 Скачать 88.36 Kb. Скачать 88.36 Kb.
|
1 2 Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Дагестанский государственный университет» Факультет математики и компьютерных наук Кафедра дифференциальных уравнений КУРСОВАЯ РАБОТА «Гармонические полиномы» по дисциплине функциональный анализ Выполнил: студент 3 курса очной формы обучения по направлению 01.03.01 – Математика Гамзатов Мадрид Велибегович Научный руководитель: Кандидат физ-матем. наук,доцент Рагимханов Вадим Римиханович Работа допущена к защите: Научный руководитель__________ «__»____________20__г. МАХАЧКАЛА – 2019 Содержание Введение…………………………………………….. 3. Оператор Лапласа в сферической системе координат… 4. Оператор Лапласа-Бельтрами на сфере и его свойства. Сферические и шаровые функции…………………8. Выражение сферических функций в сферической системе координат. Уравнение Лежандра……………………..14. Ортогональность сферических функций и функций Лежандра…………………………………………….19. Заключение…………………………………………..22. Введение В математике (общей алгебре) многочлен от нескольких переменных над полем называется гармоническим, если лапласиан этого многочлена равен нулю. Избранная схема изложения основывается на использовании элементарных свойств оператора Лапласа–Бельтрами на единичной сфере и связи собственных функций этого оператора — сферических функций с шаровыми функциями — однородными гармоническими многочленами. Для исследования поведения решений уравнения Лежандра в окрестностях особых точек привлекаются факты из аналитической теории обыкновенных дифференциальных уравнений с правильными особенностями. §1. Оператор Лапласа в сферической системе координат 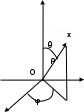 Естественно перейти в задаче к сферической Естественно перейти в задаче к сферическойсистеме координат 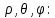 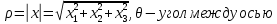  и вектором и вектором 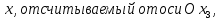 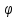 -угол между осью -угол между осью 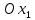 и проекцией и проекцией 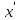 вектора вектора 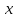 на плоскость 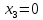 ,отсчитываемый от оси ,отсчитываемый от оси 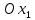 . .При этом 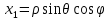 , , 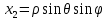 , , 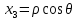 , ,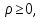 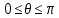 , , 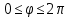 (2) (2) (при ρ = 0 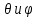 не определяются однозначно). не определяются однозначно).Выведем уравнение Лапласа в сферической системе координат. Поскольку 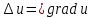 , ,то для этого следует получить выражения в сферической системе для 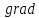 и и 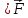 , где , где 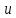 – скалярное, а – скалярное, а 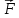 – векторное поля в Ω. – векторное поля в Ω.Если 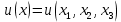 – некоторая функция в Ω, то через – некоторая функция в Ω, то через 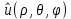 будем обозначать выражение функции будем обозначать выражение функции 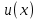 в сферической системе в сферической системе 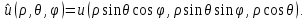 (3) (3)Итак, нам нужно получить выражение 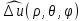 через через 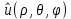 . . Обозначим через Обозначим через 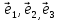 ортонормированный базис исходной декартовой системы ортонормированный базис исходной декартовой системы 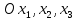 . Пусть . Пусть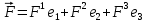 (4) (4)- некоторое векторное поле в 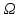 ( (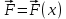 – вектор-функция на – вектор-функция на 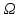 ), ),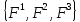 - координаты 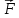 в базисе в базисе 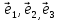 . .Каждой точке 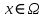 , , 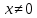 , со сферическими координатами , со сферическими координатами 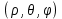 поставим в соответствие подвижный ортонормированный репер поставим в соответствие подвижный ортонормированный репер 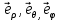 (тройку взаимно ортогональных единичных векторов): (тройку взаимно ортогональных единичных векторов):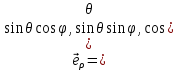 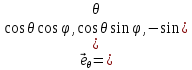 (5) (5)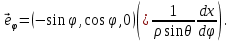 Легко видеть, что эти векторы – единичные касательные векторы соответственно к координатным линиям 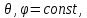 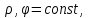 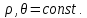 Разложим вектор 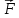 по ортонормированному базису (5) по ортонормированному базису (5)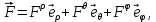 (6) (6) 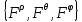 – координаты – координаты 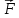 в базисе (5) или, как мы их будем называть, координаты вектора в базисе (5) или, как мы их будем называть, координаты вектора 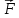 в сферической системе. в сферической системе.В силу ортонормированности репера (5) 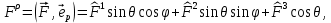 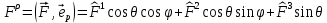 , (7) , (7)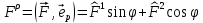 , ,Где 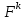 - декартовы координаты - декартовы координаты 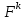 , выраженные кк скалярные функции в сферической системе. , выраженные кк скалярные функции в сферической системе.2⸰. Получим выражение координат вектора ∆u = grad u, u € С1 (Ω), в сферической системе. Дифференцируя (3) последовательно по p, 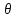 , ,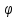 , имеем , имеем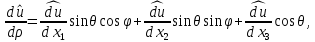 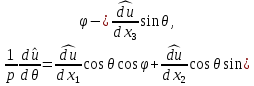 () ()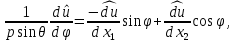 Поскольку { 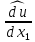 , , 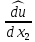 , , 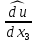 } –координаты ∆u в декартовой системе, в силу (7) получаем } –координаты ∆u в декартовой системе, в силу (7) получаем 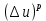 = = 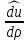 , , 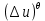 = =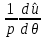 , , 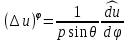 (8) (8)3⸰. Пусть теперь 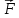 – гладкое векторное поле в Ω. Получим выражение – гладкое векторное поле в Ω. Получим выражение 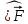 в сферической системе, т.е. выражение этой функции через в сферической системе, т.е. выражение этой функции через 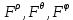 Пусть теперь  — гладкое векторное поле в Ω. Получим выражение — гладкое векторное поле в Ω. Получим выражение 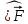 в сферической системе, т.е. выражение этой функции через в сферической системе, т.е. выражение этой функции через 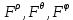 . Для этого сначала выразим . Для этого сначала выразим 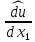 , , 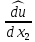 , , 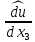 , где u — произвольная гладкая функция в Ω, через , где u — произвольная гладкая функция в Ω, через 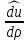 , , 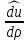 , , 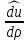 . Это легко сделать, рассматривая соотношения (8) как систему линейных уравнений относительно величин . Это легко сделать, рассматривая соотношения (8) как систему линейных уравнений относительно величин 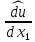 , , 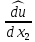 , , 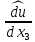 . Учитывая то, что матрица такой системы — ортогональная матрица, а обратная к ортогональной матрице является транспонированная к ней, получаем . Учитывая то, что матрица такой системы — ортогональная матрица, а обратная к ортогональной матрице является транспонированная к ней, получаем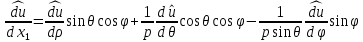 , , 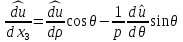 Используя эти выражения, мы получаем (выполняя на последней стадии суммирование по столбцам и тождественные преобразования) 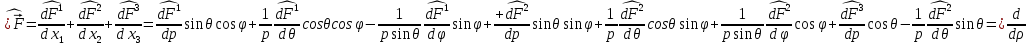 ( (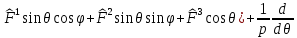 ( (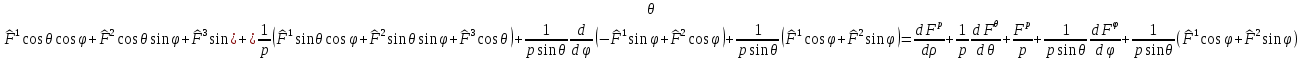 (9) (9)Остаётся последнее слагаемое здесь выразить через 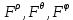 . Для этого обратимся к соотношениям (7). Умножим первое из них на . Для этого обратимся к соотношениям (7). Умножим первое из них на 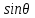 , второе — на , второе — на 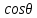 , сложим их. В результате получим , сложим их. В результате получим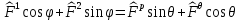 Используя это соотношение, окончательно получаем 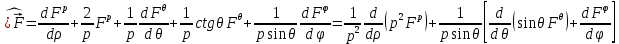 (10) (10)Это и есть выражение дивергенции векторного поля 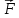 в сферической системе координат. в сферической системе координат. 4◦. Теперь уже легко выписать выражение оператора Лапласа в сферической системе. Используя (10), тождествоc 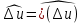 и (9), находим и (9), находим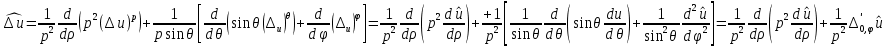 (11) (11)где мы обозначили 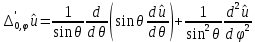 (12) (12)Итак, в сферической системе оператор Лапласа представляет собой сумму оператора 2-го порядка по радиальной переменной 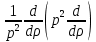 и оператора 2-го порядка по угловымпеременным и оператора 2-го порядка по угловымпеременным 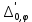 , поделённого на ρ2. Оператор , поделённого на ρ2. Оператор 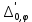 называют оператором Лапласа–Бельтрами на единичной сфере в R3. называют оператором Лапласа–Бельтрами на единичной сфере в R3. §2. Оператор Лапласа-Бельтрами на сфере и его свойства. Сферические и шаровые функции Обозначим через 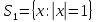 – единичную сферу в – единичную сферу в 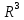 с центром в начале координат. с центром в начале координат.Определение 1. Через 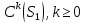 – целое, обозначим пространство функций – целое, обозначим пространство функций 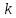 раз непрерывно дифференцируемых на раз непрерывно дифференцируемых на с  фере фере 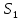      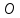 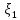 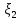 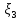 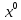 Это означает следующее. Для любой точки 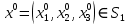 возьмем какую-нибудь декартову систему возьмем какую-нибудь декартову систему 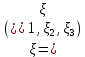 с началом в точке O , причем такую, что ось с началом в точке O , причем такую, что ось 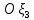 направлена по вектору направлена по вектору 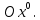 При этом плоскость При этом плоскость 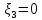 параллельна касательной плоскости к параллельна касательной плоскости к 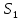 в точке в точке 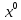 . Обозначим . Обозначим 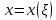 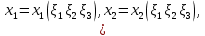 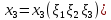 формулы перехода к новой формулы перехода к новой системе 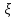 и введем в рассмотрение функцию и введем в рассмотрение функцию 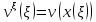 – выражение функции – выражение функции 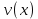 в новой декартовой системе ξ. Далее, уравнение в системе ξ куска в новой декартовой системе ξ. Далее, уравнение в системе ξ куска 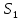 , проходящего через точку , проходящего через точку 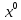 , будет , будет 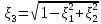 , , 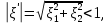 где где 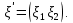 Выразим Выразим 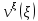 только через “касательные” координаты только через “касательные” координаты 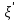 (являющиеся касательными координатами куска (являющиеся касательными координатами куска 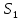 ) и получим функцию ) и получим функцию 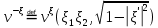 . (13) . (13)Так вот, по определению функция 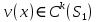 , если для любой , если для любой 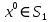 и для любой декартовой системы и для любой декартовой системы 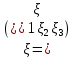 , описанной выше, функция (13) принадлежит пространству , описанной выше, функция (13) принадлежит пространству 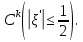 Аналогичным образом определяется пространство Аналогичным образом определяется пространство 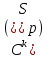 на сфере на сфере 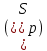 радиуса радиуса 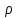 . .З а м е ч а н и е 1. Можно показать, что это определение эквивалентно также следующему. Функция 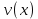 принадлежит пространству принадлежит пространству 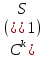 тогда и только тогда, когда для любой декартовой системы координат тогда и только тогда, когда для любой декартовой системы координат 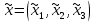 с центром в начале координат функция с центром в начале координат функция 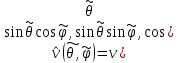 , (14) , (14)где 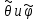 – углы в сферической системе, связанной с декартовой системой – углы в сферической системе, связанной с декартовой системой 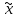 , принадлежит пространству , принадлежит пространству 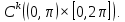 Определение 2. Оператор Лапласа – Бельтрами 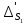 на единичной сфере на единичной сфере 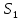 определим как оператор, переводящий всякую функцию определим как оператор, переводящий всякую функцию 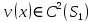 в функцию в функцию 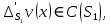 выражение которой в сферических координатах дается формулой выражение которой в сферических координатах дается формулой 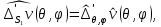 (15) (15)где 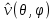 определяется по формуле (14), только без “тильд”, определяется по формуле (14), только без “тильд”, 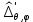 - дифференциальный оператор 2-го порядка, определяемой формулой (12). - дифференциальный оператор 2-го порядка, определяемой формулой (12).Здесь мы встречаемся по сути дела с определениями пространств гладких функций на гладком многообразии (в данном случае – на сфере 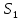 ) и дифференциального оператора на таком многообразии. ) и дифференциального оператора на таком многообразии.Хотя выражение оператора 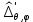 оператора Лапласа-Бельтрами оператора Лапласа-Бельтрами 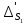 в сферической системе зависит от углов в сферической системе зависит от углов 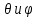 , а , а 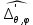 имеет особенности при имеет особенности при 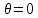 и и 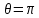 ( (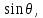 появляющийся в знаменателе, обращается в нуль в этих точках), сам оператор появляющийся в знаменателе, обращается в нуль в этих точках), сам оператор 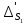 во всех точках сферы во всех точках сферы 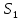 устроен совершенно одинаково. Если мы перейдем к другой сферической системе, связанной с другой декартовой системой устроен совершенно одинаково. Если мы перейдем к другой сферической системе, связанной с другой декартовой системой 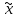 (например, с осью (например, с осью 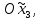 направленной по старой оси направленной по старой оси 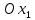 ) то ) то  уже не будет иметь особенностей в старых полюсах сферы ( уже не будет иметь особенностей в старых полюсах сферы (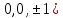 , соответствующих , соответствующих 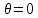 и и 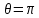 . .Эту “одинаковую устроенность” оператора 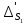 во всех точках во всех точках 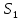 можно легко уяснить также из формулы можно легко уяснить также из формулы 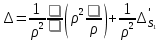 . .Оператор Лапласа 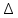 инвариантен (не изменяет своей формулы) относительно вращений (т.е при переходе к другой ортогональной системе инвариантен (не изменяет своей формулы) относительно вращений (т.е при переходе к другой ортогональной системе 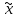 с центром в начале координат), оператор с центром в начале координат), оператор 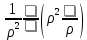 содержит дифференцирования только по радиусу и очевидно инвариантен относительно вращений. Отсюда и оператор содержит дифференцирования только по радиусу и очевидно инвариантен относительно вращений. Отсюда и оператор 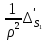 , а с ним и оператор , а с ним и оператор 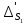 инвариантен относительно вращений. инвариантен относительно вращений.Нетрудно установить, что оператор 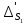 отображает пространство отображает пространство 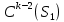 . .Имеет место следующее утверждение. Лемма 1. Оператор 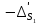 симметричен и неотрицателен на пространстве симметричен и неотрицателен на пространстве 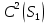 относительно скалярного произведения в относительно скалярного произведения в 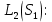 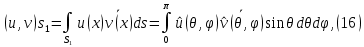 а именно, 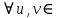 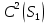 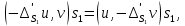 ( 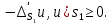 (17) (17) Д о к а з а т е л ь с т в о. В силу определения оператора 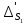 для любых для любых 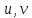 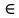 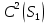 имеем имеем( 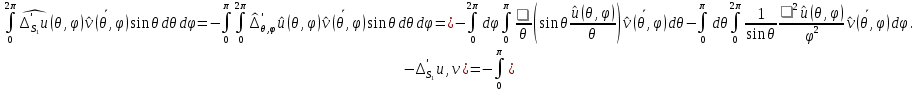 (18) (18)Покажем, что все функции, которые стоят под знаками интегралов в последнем выражении, на самом деле не имеют особенностей и принадлежит пространству 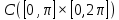 как функции как функции 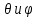 .В самом деле, например, .В самом деле, например,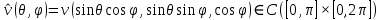 как суперпозиция непрерывных функций. Аналогично для 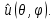 Проверим далее, что функции 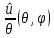 и и 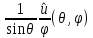 (19) (19) принадлежит 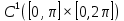 . Отсюда будет следовать, что и . Отсюда будет следовать, что и 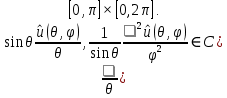 В силу сделанного выше замечания 1 функция 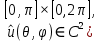 а потому а потому 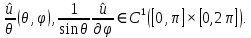 Поэтому остается показать, например, что функция (19) принадлежит пространствам 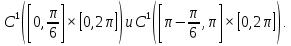 Лемма 2. 1  . Собственные значения (СЗ) оператора . Собственные значения (СЗ) оператора 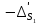 неотрицательны. неотрицательны.2  Собственные функции (СФ) оператора Собственные функции (СФ) оператора 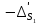 , отвечающие различными СЗ, ортогональны относительно скалярного произведения (16). , отвечающие различными СЗ, ортогональны относительно скалярного произведения (16).Д о к а з а т е л ь с т в о. 1  . Пусть . Пусть 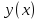 – СФ оператора – СФ оператора 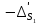 , отвечающая СЗ , отвечающая СЗ  : :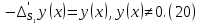 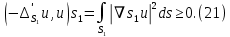 Последнее влечет, что  Тогда в силу (20) и (21) Тогда в силу (20) и (21)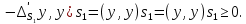 Отсюда вытекает, что и 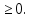 2  Пусть Пусть 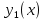 и и 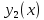 – две СФ оператора – две СФ оператора 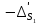 , отвечающие, соответственно, СЗ , отвечающие, соответственно, СЗ 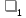 и и 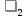 причем причем 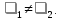 Тогда пользуясь симметричностью Тогда пользуясь симметричностью 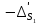 и действительностью СЗ и действительностью СЗ 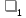 и и 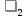 имеем: имеем: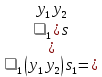 ( (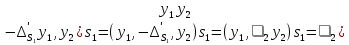 ) )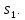 Отсюда 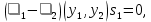 и поскольку 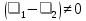 , , 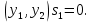 Лемма установлена. Лемма установлена.Лемма 3. 1 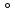 . Собственными значениями оператора . Собственными значениями оператора 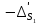 могут быть лишь числа могут быть лишь числа 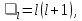 где где 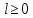 – целые. Если – целые. Если 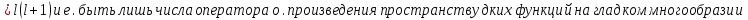 - СЗ, 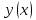 – соответствующая ему СФ оператора – соответствующая ему СФ оператора 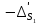 , то функция , то функция 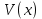 , имеющая в сферической системе координат выражение , имеющая в сферической системе координат выражение где 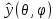 – выражение в сферической системе на – выражение в сферической системе на 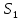 СФ СФ 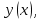 представляет собой однородный гармонической многочлен переменных представляет собой однородный гармонической многочлен переменных 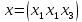 степени степени 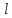 2  Обратно, если V(x) – ненулевой Обратно, если V(x) – ненулевой 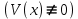 однородный гармонический многочлен в однородный гармонический многочлен в 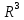 степени степени 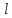 , то его представление , то его представление 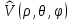 в сферической системе имеет вид (22), где в сферической системе имеет вид (22), где 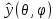 – выражение в сферической системе на – выражение в сферической системе на 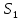 функции функции 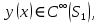 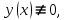 представляющей собой СФ оператора - представляющей собой СФ оператора - 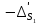 , отвечающую СЗ , отвечающую СЗ 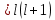 . .Определение 3. Всякую собственную функцию 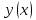 оператора оператора 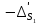 , отвечающую собственному значению , отвечающую собственному значению 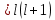 , ,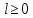 – целое, будем называть сферической функцией веса – целое, будем называть сферической функцией веса 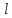 Обычно сферической функцией называют также и выражение 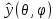 функции функции 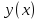 в сферической системе. в сферической системе.Лемма 3 по сути дела и дает описание множества сферических функций. А именно, имеем следующее Следствие 1. Множество всех сферических функций веса 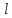 представляет собой совокупность следов на 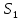 всех ненулевых однородных гармонических многочленов на всех ненулевых однородных гармонических многочленов на 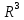 степени степени 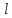 . .Определение 4. Пусть 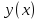 – сферическая функция веса – сферическая функция веса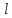 . Однородный гармонический многочлен, имеющий в сферической системе выражение (22), называют шаровой функцией, порожденной . Однородный гармонический многочлен, имеющий в сферической системе выражение (22), называют шаровой функцией, порожденной 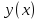 . . 1 2 |
