КУРСОВАЯ РАБОТА: Гармонические полиномы. Курсовая Работа.Гамзатов М.В. 3К1ГР. Курсовая работа Гармонические полиномы
 Скачать 88.36 Kb. Скачать 88.36 Kb.
|
1 2 Пусть 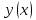 – сферическая функция веса – сферическая функция веса 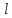 , ,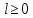 – целое, а – целое, а 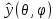 – ее выражение в сферической системе. – ее выражение в сферической системе. 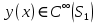 как в след гармонического многочлена и, кроме того, как в след гармонического многочлена и, кроме того, 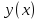 – СФ оператора – СФ оператора 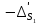 , отвечающая СЗ , отвечающая СЗ 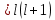 . Поэтому . Поэтому 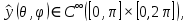 заведомо ограниченная функция, заведомо ограниченная функция, 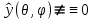 , и удовлетворяет уравнению , и удовлетворяет уравнению 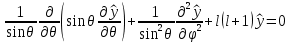 (1) (1)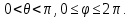 Нам достаточно найти 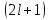 линейно независимых функций, удовлетворяющих этим условиям. Будем искать каждую такую функцию методом разделения переменных в виде линейно независимых функций, удовлетворяющих этим условиям. Будем искать каждую такую функцию методом разделения переменных в виде 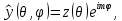 m – целое (2) m – целое (2)В силу бесконечной дифференцируемости 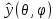 функция функция 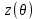 также обязана принадлежать также обязана принадлежать 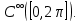 Подставляя (2) в (1) и сокращая на Подставляя (2) в (1) и сокращая на 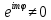 , приходим к обыкновенному дифференциальному уравнению , приходим к обыкновенному дифференциальному уравнению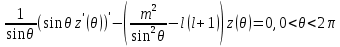 где 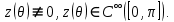 (3) (3)В этом уравнении удобно сделать замену независимой переменной 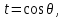 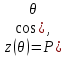 -1 -1которая преобразует уравнение (3) к уравнению 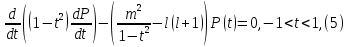 причём P(t)∈ 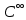 ((−1,1)) и ограниченная на (−1,1) функция, P(t)≢0. Уравнение (5) называется уравнением Лежандра. ((−1,1)) и ограниченная на (−1,1) функция, P(t)≢0. Уравнение (5) называется уравнением Лежандра.Итак, перейдём к нахождению таких решений уравнения (5). Умножив это уравнение на ( 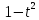 ), преобразуем его к форме ), преобразуем его к форме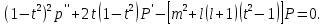 (6) (6)Существует аналитическая теория обыкновенных дифференциальных уравнений, в которой имеется раздел, посвящённый аналитической теории линейных уравнений с правильными особыми точками, см., например, книги [4] или [5] из списка литературы, приведённого в конце данного пособия. По этой теории, если в окрестности некоторой точки c линейное дифференциальное уравнение может быть приведено к виду. 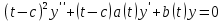 (7) (7)где 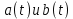 — некоторые функции t, аналитические в некоторой окрестности точки — некоторые функции t, аналитические в некоторой окрестности точки 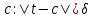 , т.е. функции, которые представимы в этой окрестности степенными рядами , т.е. функции, которые представимы в этой окрестности степенными рядами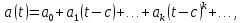 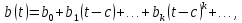 то точку 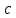 называют правильной особой точкой уравнения (6). называют правильной особой точкой уравнения (6).В этом случае уравнение (45) (поскольку 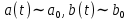 при при 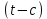 малых) похоже в малой окрестности точки малых) похоже в малой окрестности точки 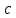 на уравнение Эйлера на уравнение Эйлера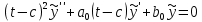 (8) (8)Решения последнего уравнения, как известно, следует искать в виде 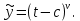 Подставляя такую функцию в уравнение (8) и сокращая на Подставляя такую функцию в уравнение (8) и сокращая на 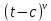 , приходим к следующему характеристическому уравнению для определения показателя , приходим к следующему характеристическому уравнению для определения показателя 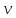 : :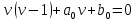 (9) (9)Это квадратное уравнение имеет два корня 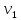 и и 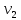 . Занумеруем их так, чтобы . Занумеруем их так, чтобы 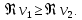 Оказывается, что так же, как и для уравнения Бесселя (для которого точка 0 является правильной особой точкой), для корня Оказывается, что так же, как и для уравнения Бесселя (для которого точка 0 является правильной особой точкой), для корня 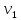 можно всегда найти решение уравнения (7) вида можно всегда найти решение уравнения (7) вида 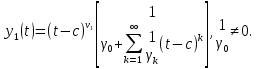 (10) (10)При этом 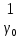 можно взять произвольным, коэффициенты можно взять произвольным, коэффициенты 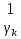 , , 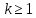 , определяются тогда уже однозначно, и степенной ряд в представлении , определяются тогда уже однозначно, и степенной ряд в представлении 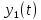 сходится в некоторой достаточно малой окрестности точки сходится в некоторой достаточно малой окрестности точки 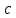 . .Что касается решения 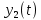 , отвечающего второму корню , отвечающего второму корню 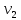 характеристического уравнения (9), то тут ситуация несколько более сложная. Если характеристического уравнения (9), то тут ситуация несколько более сложная. Если 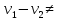 целому. То существует и второе решение целому. То существует и второе решение 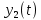 уравнения вида (10), но с уравнения вида (10), но с 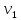 и и 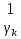 замененными, соответственно, на замененными, соответственно, на 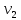 и и 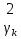 , и потому в этом случае , и потому в этом случае 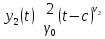 в окрестности точки в окрестности точки 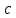 . Если же . Если же 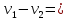 целому целому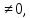 то оказывается также существует решение то оказывается также существует решение 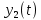 уравнения (7), которое имеет поведение уравнения (7), которое имеет поведение 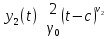 при при 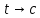 . В случае же, когда . В случае же, когда 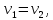 и второе решение уравнения (7) линейно независимое с и второе решение уравнения (7) линейно независимое с 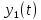 , имеет уже в малой окрестности точки , имеет уже в малой окрестности точки 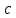 такое поведение: такое поведение: 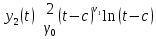 Обратимся к уравнению Лежандра в форме (6). У этого уравнения две особые точки 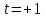 и и 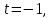 поскольку коэффициент при поскольку коэффициент при 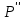 обращается в нуль только в этих точках. Эти особые точки являются правильными. Проверим это, например, для точки обращается в нуль только в этих точках. Эти особые точки являются правильными. Проверим это, например, для точки 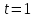 . .Разделим уравнение (6) на функцию 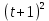 , которая не обращается в нуль в окрестности исследуемой точки t = 1. Уравнение приобретает вид , которая не обращается в нуль в окрестности исследуемой точки t = 1. Уравнение приобретает вид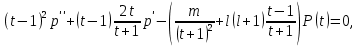 т.е становится вида (6) с 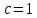 и с (11) и с (11)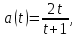 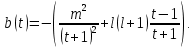 Нетрудно видеть, что 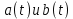 — регулярные функции переменной t (рассматриваемой уже как комплексная переменная) в круге — регулярные функции переменной t (рассматриваемой уже как комплексная переменная) в круге 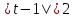 . Поэтому эти функции допускают разложения в этом круге в ряды Тейлора . Поэтому эти функции допускают разложения в этом круге в ряды Тейлора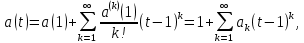  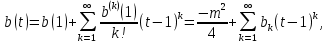 И следовательно, и для действительных 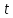 в окрестности в окрестности 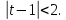 Итак, точка Итак, точка 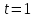 является правильной. является правильной.Поэтому согласно сформулированной выше теории уравнение (11) при 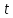 , близких к 1,становится похожим на уравнение Эйлеровского типа , близких к 1,становится похожим на уравнение Эйлеровского типа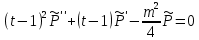 (12) (12)Решение последнего уравнения ищем в виде 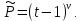 И, как и выше для И, как и выше для 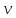 , получаем квадратное уравнение для: , получаем квадратное уравнение для: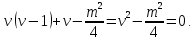 Это уравнение имеет два корня 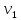 и и 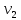 , ,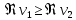 : :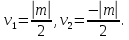 При этом, как это следует из сказанного выше, тогда всякое ограниченное в окрестности точки 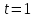 решение уравнения (11) имеет вид решение уравнения (11) имеет вид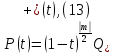 где функция 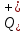 (t) аналитическая, а потому и бесконечно (t) аналитическая, а потому и бесконечнодифференцируемая функция в окрестности точки t = 1. Действительно, одно нетривиальное решение уравнения (11) согласно этой формуле имеет (13), а другое решение, линейно независимое с этим имеет поведение 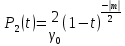 при при 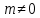 и и 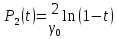 при при 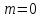 , а потому это второе решение неограниченно в окрестности точки , а потому это второе решение неограниченно в окрестности точки 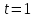  Лемма 4. 1 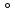 . Если . Если 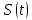 – решение уравнения – решение уравнения 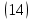 , то , то 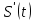 является решением уравнения вида (14) с является решением уравнения вида (14) с 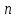 , замененным на , замененным на 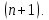 2 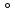 . При . При 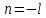 решением уравнения (14) является многочлен решением уравнения (14) является многочлен 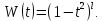 (15) (15)Д о к а з а т е л ь с т в о.1 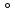 . Если . Если 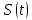 – решение уравнения (14), то дифференцируя его (как тождество), получим – решение уравнения (14), то дифференцируя его (как тождество), получим 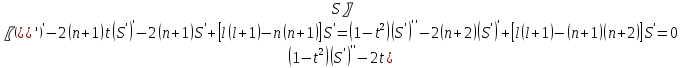 , ,и первое утверждение леммы установлено. 2 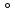 . Преобразуем уравнение (14) при . Преобразуем уравнение (14) при 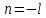 к виду к виду 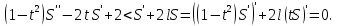 Поэтому решение уравнения первого порядка: 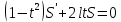 будет и решением предыдущего уравнения. Но последнее уравнение легко интегрируется (оно является уравнением с разделяющимися переменными). Одним из решений этого уравнения является функция (15). Лемма 4 установлена. §4. Ортогональность сферических функций и функций Лежандра. Итак, обозначим через 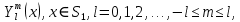 (1) (1)систему всех сферических функций, каждая из которых - 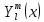 имеет в сферической системе выражение (*) имеет в сферической системе выражение (*)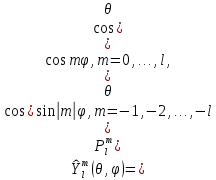 (*) (*)Лемма 5. Система (1) сферических функций является ортогональной системой относительно скалярного произведения (§2.(16). 2  . Имеют место равенства . Имеют место равенства 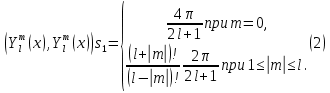 Д о к а з а т е л ь с т в о. Установим сначала 1 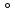 , а именно , что , а именно , что 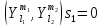 для любых для любых 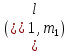 и и 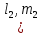 ) таких, что либо ) таких, что либо 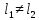 либо либо 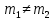 . Если . Если 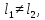 то поскольку то поскольку 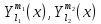 – собственные функции оператора – собственные функции оператора 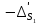 , отвечающие различным собственным значениям , отвечающие различным собственным значениям 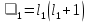 и и 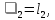 в силу леммы 2 в силу леммы 2 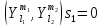 Пусть далее 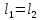 но но 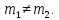 Рассмотрим случай Рассмотрим случай 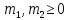 . Выполняя замену . Выполняя замену 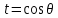 , получаем для , получаем для 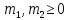 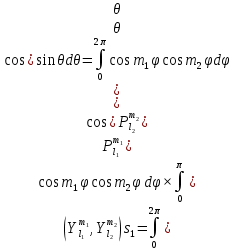 (3) (3) Поэтому для 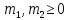 , , 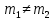 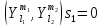 в силу известного из курса математического анализа свойства ортогональности классической тригонометрической системы в силу известного из курса математического анализа свойства ортогональности классической тригонометрической системы 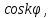 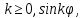 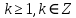 на интервале на интервале 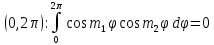 при при 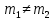 . Совершенно аналогично рассматриваются другие возможности для случая . Совершенно аналогично рассматриваются другие возможности для случая 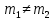 . Итак, 1◦ установлено.Отметим, что из этого свойства вытекает непосредственно свойство ортогональности систем многочленов Лежандра и присоединённых функций Лежандра на интервале (−1,1). . Итак, 1◦ установлено.Отметим, что из этого свойства вытекает непосредственно свойство ортогональности систем многочленов Лежандра и присоединённых функций Лежандра на интервале (−1,1).Лемма 6. При каждом фиксированном 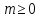 , ,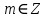 , ,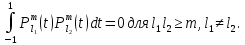 (4) (4)Д о к а з а т е л ь с т в о. Обратимся к формуле (3). Поскольку 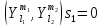 , а , а 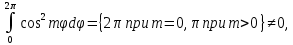 получаем (4). получаем (4).Справедливость утверждения 2◦ леммы 7 непосредственно вытекает из формулы (3) и её аналога при 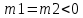 и нижеследующего утверждения. и нижеследующего утверждения.Лемма 7. Для любых целых 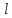 и и 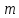 , ,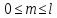 имеет место равенство имеет место равенство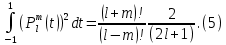 Для доказательства этой формулы удобно воспользоваться рекуррентной формулой для многочленов Лежандра, выражающей 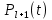 через через 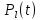 и (t). Доказательство такой формулы в свою очередь легко следует из нижеследующего разложения, которое представляет и самостоятельный интерес. и (t). Доказательство такой формулы в свою очередь легко следует из нижеследующего разложения, которое представляет и самостоятельный интерес.Лемма 8. Для любых 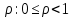 справедливо разложение справедливо разложение 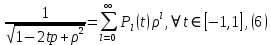 причем это разложение допускает по членное дифференцирование по 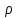 и по и по 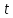 произвольное число раз. произвольное число раз. Заключение В данной курсовой работе мы рассмотрели операторы: Лапласа и Лапласа-Бельтрами. Оператор Лапласа: С помощью данного оператора удобно записывать уравнения Лапласа, Пуассона и волновое уравнение. В физике оператор Лапласа применим в электростатике и электродинамике, квантовой механике, во многих уравнениях физики сплошных сред, а также при изучении равновесия мембран, плёнок или поверхностей раздела фаз с поверхностным натяжением в стационарных задачах диффузии и теплопроводности, которые сводятся, в непрерывном пределе, к обычным уравнениям Лапласа или Пуассона или к некоторым их обобщениям. Сферические функции представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями и при решении физических задач, обладающих сферической симметрией. Сферические функции имеют большое значение в теории дифференциальных уравнений в частных производных и теоретической физике, в частности в задачах расчёта электронных орбиталей в атоме, гравитационного поля геоида, магнитного поля планет и интенсивности реликтового излучения 1 2 |
