Курсовая работа имитационное моделирование акций компании Дисциплина Экспериментальное моделирование
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
1 2 Метод Монте-Карло – это математический метод, где основой служат понятия из теории вероятности и математической статистики. Если быть точнее, то при помощи данного метода можно решать математические задачи используя моделирования случайных чисел []. Многие понимают под данным методом – метод статистических испытаний. Но было бы ошибкой называть его так, так как метод статистических испытаний подразумевает под собой более широкое применение, ведь он может использоваться как математической моделью изучаемого объекта, следовательно, метод Монте-Карло, так и в процессе настоящих опытов. В последнем случае все проверки исполняются на настоящем объекте изучения. По итогу исследователь получает самую полную и точную информацию о поведении изучаемого объекта. Но, нужно заметить, что настоящий эксперимент очень дорого обходится в материальном плане, в иных случаях это может привести к различным катастрофам техногенного характера []. Официальной на сегодняшний день датой появления метода Монте-Карло можно считать 1949 год, в то время была опубликована статья в таком журнале как «Journal of American Statistical Association» С. Улама и Н. Метрополиса. Но, а сама терминология появилась еще во время Второй мировой войны, тогда Джон фон Нейман и Станислав Марцин работали в Лос-Аламосе в США и разрабатывали нейтронную диффузию в расщепляемом материале, с Н. Метрополис, Г. Каном и Э. Ферми создать первую атомную бомбу. Свое название данный метод получил из-за названия района и города Монте-Карло. Монте-Карло – является одним из крупнейших в мире, а также самым крупным в Европе игорным центром, находится игорный центр на территории княжества Монако. Город получил название в 1866 году по имени первого казино, открытого в 1860 году []. Понятие Монте-Карло напрямую сопряжено с игорным бизнесом, которому в принципе люди и обязаны возникновением теории вероятности и математической статистики. Человек всегда хотел обмануть случайность. И это не зависело от того, играет ли он в казино или же сталкивается с совершенно случайным событием, к примеру, в поиске предмета нам предстоит ожидать счастливого случая, который может наступить, а может и не наступить. Метод Монте-Карло относится к численным методам, который использует моделирование исходных случайных величин и последующее их математическое изменение в соответствии с изучаемой процедурой и построением полученных статистических оценок для требуемых величин. Данный метод, является почти той самой игорной рулеткой, где процесс будет повторяться многократно. Итоги таких игр копятся, проходят анализ и на основе исследований происходят итоги о оптимальной стратегии исполнения каких-либо операций []. Главная концепция метода заключается в применение выборки случайных чисел для извлечения искомых оценок. Чтобы не описывать текущий процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), происходит «розыгрыш» рандомных событий при помощи особого организованного процесса в который входит случайность и предоставляющий совершенно случайный итог. По сути, метод Монте-Карло может решить любую задачу на вероятность, но все же данный метод может быть оправдан только когда процесс «розыгрыша» легче, а не сложнее аналитических расчетов. По мнению, некоторых экспертов в области моделирования, метод Монте-Карло имеет несколько преимуществ, если сравнивать с остальными методами анализа количественного анализа риска. Когда используется данный метод, разделение всех возможных итогов событий производится многократный анализ, но обстоятельства должны быть такими, что постоянно используются входные данные, подобранные случайно из распределений вероятности элементов, которые составляют эту модель. Особенно полезен данный метод может быть в определенной ситуации и решения, связанных с ним вопросов. В пример можно поставить два альтернативных проекта, где основным параметром эффективности будет потенциальная прибыль, зависящая от многих факторов (доля рынка, реклама, издержки, затраты, срок службы и др.). В таких ситуациях у людей, которые принимают основные решения, могут возникнуть основательные проблемы в правильной оценки прибыли, которая может быть получена. Для принятия решения и ответа на вопрос, а сможет ли текущий проект принести добавленную стоимость, менеджер должен определить все условия, которые могли бы повлиять на прибыль, а уже после изучить большое количество вариантов комбинаций этих факторов на уровень прибыли, что в целом и отражает присутствие риска. Из-за такой обстановки, все же рекомендуют поделить проблему на несколько мелких частей, дать оценку распределение вероятности для основных условий, воздействующих на модель. К примеру, вероятности вероятных частей на рынке, объемов производства продукции, инвестиционных затрат и т.д. Как только были установлены вероятности для ключевых условий модели мы может по итогу установить их общий эффект для извлечения вероятного распределения прибыли. Главная проблема применения классического сценарного анализа с целью оценки риска заключается в огромном количестве условий и из-за того, что некоторые могут повлиять на ценность других условий, количества вероятных комбинаций, которые имею шанс оказать влияние на итог показателя эффективности проекта стремится к бесконечности. Решение текущей проблемы является ключевым превосходством имитационного моделирования методом Монте-Карло. Такое осуществления моделирования, как было сказано до этого, базируется на том, что при известных законах распределения переменных возможно приобрести не одно значение, а множество распределение результирующего показателя для не имеющего границ разных сценариев []. Схема применения метода Монте-Карло в количественном анализе рисков такова: делается математическая модель результирующего показателя как метода от переменных и условий. Переменной считается какое-то случайное число нашего проекта, условиями – те значения, которые могут быть детерминированы. Математическая модели изменяется и происходят новые расчеты постоянно при каждом новом имитационном эксперименте, все время которого числа ключевых неясных переменных отбираются случайным способом на базе формирования случайных значений. Как итог результаты всех имитаций объединяются в выборку и дальше происходит анализ с помощью статистических методов с целью получения вероятностей результирующего показателя и расчета ключевых измерителей риска проекта []. Блок схему моделирования методом Монте-Карло можно представить в следующем виде, как показано на рисунке 1. 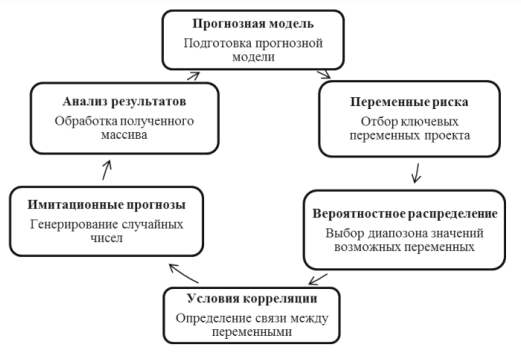 Рисунок 1 –Блок-схема метода Монте-Карло Но вскоре возникает другая проблема, состоящая в том, что чтобы применить модель Монте-Карло понадобится множество вычислений. Но все же проблема решается с помощью компьютера, а именно благодаря установленному на нем программному обеспечению, которое поможет создать огромное количество возможных комбинаций, характеристики которых можно задать самостоятельно. Поэтому, чем точнее заданные входные характеристики, тем точнее будет предусмотрен риск при оценки проекта. На сегодняшний день существует множество программного обеспечения для имитационного моделирования методом Монте-Карло (Alt-Invest, ИНЭК-Аналитик, Project Expert и др.), которые дают человеку возможность для анализа критических условий, которые влияют на уровень риска, следовательно, это помогает осуществлять тактические решения с целью достижения установленных целей в обстоятельствах высочайшего уровня неопределенности рыночных факторов []. Сущность метода Монте-Карло заключается в том: необходимо отыскать значение m определенного размера. Для этой цели отбирается специальная абсолютно случайная величина X, математическое ожидание которой равно m:  На практике все же происходит так: делают неопределенное количество n испытаний, где по итогу получается n вероятных значений X, происходит расчет их среднего арифметического, где получают его в качестве значения искомого значения m. [] 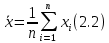 где 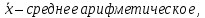 n – количество испытаний,  При помощи генератора случайных вместе с функцией распределения вероятностей чисел мы можем получать данные искусственным путем для изучаемой процедуры. В качестве генератора можно взять таблицы случайных чисел, рулетку или программу на компьютере или то, что может дать равномерное распределение. Доступное разыгрыванию распределение вероятностей может быть показано на эмпирических данных, которые были извлечены из ранее сформированных данных или же может быть результат прошедшего эксперимента []. Следовательно, чтобы применить метод Монте-Карло нам понадобится умение разыграть случайное число. В сфере образования метод Монте-Карло представляет наибольший интерес как вычислительное устройство для выполнения статистических выводов. Многие интересные модели имеют чрезвычайно сложную структуру и не могут быть легко обработаны с помощью традиционных методов. В рамках байесовской парадигмы вся информация, на которой может основываться вывод, кодируется в рамках апостериорного распределения вероятностей. Используя метод Монте-Карло, мы можем охарактеризовать эти распределения и рассчитать ожидания для них: основной метод вывода. Можно привести следующий пример. Метод Монте-Карло обращает обычную проблему статистики: вместо оценки случайных величин детерминированным образом случайные величины используются для оценки детерминированных величин. Например, в одном простом эксперименте Монте-Карло рассматривается дождь, который падает равномерно случайным образом (т. е. положение любой капли дождя можно интерпретировать как реализацию равномерно распределенной случайной величины) над некоторой квадратной областью пространства, и круг, вписанный в этот квадрат. Без ссылки на какую-либо формальную теорию вероятности интуитивно понятно, что вероятность того, что однородная капля дождя упадет в любой области внутри квадрата, должна быть пропорциональна площади этой области и не зависит от ее местоположения. Следовательно, вероятность p, то, что капля дождя находится внутри вписанного круга, может быть выражено через их площади. Если квадрат имеет стороны длины 2r, окружность должна быть радиуса r. 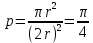 (2.3) (2.3)Само по себе это может показаться не особенно интересным. Однако, выразив π как функцию этой вероятности, ее оценки можно использовать для аппроксимации π. Действовать аналитически невозможно: для получения вероятности требуется знание π. Интуитивно можно оценить эту вероятность, подсчитав долю дождевых капель, лежащих внутри круга: если наблюдается n дождевых капель и m из них лежат внутри круга, то можно оценить p. 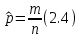 А теперь разберем те самые правила для разыгрывания случайных величин. Перед началом отметим, что R – непрерывная случайная величина, которая будет разбросана на величине (0, 1), а 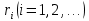 – будут случайными числами, которые могут быть возможными значениями R. – будут случайными числами, которые могут быть возможными значениями R.Правило 1. Для разыгрывания случайной величины X, которая установлена законом распределения нужно: Разделить промежуток (0, 1) оси Or на n выборочных интервалов; Сделать выбор случайного числа  из любого генератора случайных чисел, это может быть любая программа или вообще данные из таблицы чисел. из любого генератора случайных чисел, это может быть любая программа или вообще данные из таблицы чисел.В случае, когда  попадает в выборочный интервал, то величина принимает допустимое значение попадает в выборочный интервал, то величина принимает допустимое значение  . .Правило 2. Является методом обратных функций. То есть чтобы получить наше значение понадобится разыграть возможное значение  непрерывной случайной величины X, при этом помня ее функцию распределения F(x). Понадобится отобрать случайное число непрерывной случайной величины X, при этом помня ее функцию распределения F(x). Понадобится отобрать случайное число  , поставить в один ряд его функции распределения и решить сравнительно , поставить в один ряд его функции распределения и решить сравнительно  уравнение которое мы получили уравнение которое мы получили 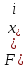 . .Правило 3. Чтобы разыграть случайное значение  непрерывной случайное величины X, при этом нужно знать ее плотность вероятности непрерывной случайное величины X, при этом нужно знать ее плотность вероятности 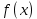 , понадобится подобрать случайное число , понадобится подобрать случайное число  и решить относительно нашего случайного числа уравнение и решить относительно нашего случайного числа уравнение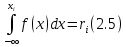 или уравнение 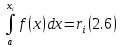 где a – наименьшее выходное значение X. Для того, чтобы смоделировать случайный процесс нам понадобятся для этого случайные числа. Так как, когда начинаются вычисления в методе Монте-Карло большинство операций используются для манипулирования случайными числами, то наличие элементарных и экономичных способов развития ряда случайных чисел во большинстве случаев устанавливает возможность использовать этот метод на практике. Для исходной совокупности случайных чисел, которые используются для создания случайных компонентов разной природы, понадобится подобрать такую совокупность, которую можно будет получить с минимальными, по возможности, расходами машинного времени, и еще гарантировать легкость и практичность будущих переустройств. В большинстве случаев полагают, что данным требованиям подходит совокупность случайных чисел, где присутствует равномерное распределение в интервале (0, 1). Отталкиваясь от равномерно распределенных случайных чисел, можно строить как случайные события, которые будут возникать при определенной заданной вероятности, так и случайные величины, владеющие большинства законов распределения. Величина R располагается на всей границе (a, b), если ее функция плотности равна: 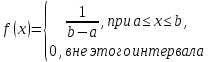 (2.7) (2.7)Функция случайное величины Rимеет вид: 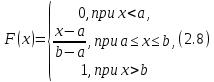 Принято брать в качестве стандартной непрерывную случайную величину 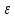 , которая равномерно разбросана на границах от 0 до 1. Но иногда все же используется дискретная случайная величина , которая равномерно разбросана на границах от 0 до 1. Но иногда все же используется дискретная случайная величина 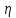 , которая с равной вероятностью будет принимать 10 значений от 0, 1, …., 9. Величина , которая с равной вероятностью будет принимать 10 значений от 0, 1, …., 9. Величина 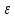 – случайное число, – случайное число, 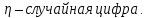 Редко Редко 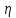 называется десятичной случайное цифрой, для того чтобы можно было ее отличить от двоичной случайной цифры. Для установления связи между называется десятичной случайное цифрой, для того чтобы можно было ее отличить от двоичной случайной цифры. Для установления связи между 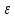 и и  нужно будет разложить ее в бесконечную десятичную дробь: нужно будет разложить ее в бесконечную десятичную дробь: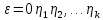 Последняя запись означает следующее: 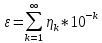 Теорема. Десятичные цифры 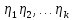 – случайного числа – случайного числа 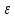 предполагает под собой независимые случайные цифры. Наоборот, если предполагает под собой независимые случайные цифры. Наоборот, если 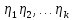 – будут независимыми случайными числами , то – будут независимыми случайными числами , то 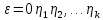 , устанавливает случайные числа. , устанавливает случайные числа.Постоянно применяются числа с окончательным числом десятичных знаков в вычислениях, из-за этого взамен случайных чисел 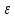 используются окончательные десятичные дроби используются окончательные десятичные дроби 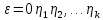 . .Таблицы случайных чисел. Допустим такое, что мы сделали несколько N независимых испытаний, где по итогу получаем несколько N независимых случайных чисел 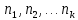 . Когда мы записываем эти числа в порядке их розыгрыша испытаний, это и будет наша таблица. . Когда мы записываем эти числа в порядке их розыгрыша испытаний, это и будет наша таблица. Рисунок 2 – Таблица случайных чисел Данной таблицей пользоваться очень просто и не возникнет труда. Когда нам понадобится во время расчета взять случайную величину, нам лишь потребуется обратится к этой таблице и взять оттуда любое число. Когда нам потребуется случайное число 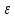 , то мы спокойно можем брать из таблицы n очередных цифр, что , то мы спокойно можем брать из таблицы n очередных цифр, что 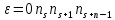 . Стоит отметить, что отбирать числа в случайной последовательности вовсе не имеет смысла. Безусловно разрешается начать с любой точки таблицы, читать в любом направлении, любого предварительно заданного алгоритма выбора, который бы не имел зависимости от конкретного числа таблицы. . Стоит отметить, что отбирать числа в случайной последовательности вовсе не имеет смысла. Безусловно разрешается начать с любой точки таблицы, читать в любом направлении, любого предварительно заданного алгоритма выбора, который бы не имел зависимости от конкретного числа таблицы.Все что было описано выше относится в основном к «идеальной» таблице случайных чисел. Чтобы составить хорошую таблицу потребуется очень много времени и не факт, что это получится так как возможно различного рода ошибки. Проверка ее на правильность необходимая в любом случае. Чтобы проверить существуют несколько таких тестов. Достоинства: проверка производится один раз воссоздавать числа можно Недостатки: запасы значения ограничены требуется много места в накопителе или же медленно вводится понадобится внешняя память Можно сделать таблицу любого объема, если возникнет потребность. Датчик случайных чисел. В большинстве случаев для создания датчика используются «шумящие» радиоэлектронные приборы. В основном датчики случайных чисел содержат m генераторов описанного типа, которые работаю в независимости, поэтому датчики выдают близкое случайное число 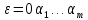 , записанное в форме m-разрядной двоичной дроби. В накопителе существует особенная ячейка, которая предназначена для случайного числа. Скорость их генерации очень высокая, что при каждом такте в работе ЭВМ записывается новое рандомное число. , записанное в форме m-разрядной двоичной дроби. В накопителе существует особенная ячейка, которая предназначена для случайного числа. Скорость их генерации очень высокая, что при каждом такте в работе ЭВМ записывается новое рандомное число.Достоинства: нету ограничений на запас числа очень быстрый вывод не расходует дополнительного места в накопителе Недостатки: постоянные проверки воссоздавать числа запрещено нужные специальные устройства Псевдослучайные числа. Данные числа получаются в результате удовлетворения каким-либо тестам. Числа, которые получаются в результате вычисления из какой-нибудь формулы, возможно использовать как случайные числа. Достоинства: проверяется один раз возможность воссоздать число получается крайне быстро занимает немного места нет необходимости во внешних устройствах Недостатки – ограниченный запас чисел. Псевдослучайные числа являются самым простым и удобным методом с точки зрения практической. Данное подтверждение можно заметить и в расчетах используя метод Монте-Карло. 3 Имитационное моделирование цены акций компании «Tesla» Как только предприятие начинается развиваться большими темпами и расширяться, руководство компании начинает задумывается выходить на фондовые рынки. Выйдя на фондовый рынок или же IPO, компания может начать зарабатывать, гораздо больше и капитализация компании начинает расти. Акция – это ценная бумага, если говорить простым языком. Должна выпускаться всегда юридическим лицом. Когда вы покупаете акцию компании, вы становитесь ее владельцем, а значит у вас на руках получается доля компании, которая рассчитывается процентом от приобретенных вами акций от общей капитализации компании. Компания может иметь сколько угодно акций, но все упирается в правовой статус компании, которая может быть как ЗАО, когда акции находятся в собственности только у сотрудников или у определенных людей. А может быть ОАО или ПАО, где акциями могут владеть неопределенное число людей. Для того, чтобы рассчитать цену акции в будущем, мы будем использовать метод Монте-Карло. В данной курсовой работе будут использовать данные акций компании «Tesla». Tesla – компания занимается производством электромобилей, которые имею название самой же компании и проектами по хранению электроэнергии. Также является лидером и самым крупным производителем электромобилей. А в 2021 году вышла на первое место по капитализации среди компаний производителей автомобилей. Для того, чтобы провести нужные нам расчеты методом Монте-Карло, будет использовано программное средство Microsoft Excel и все необходимые данные компании «Tesla» находящиеся в открытом доступе. Внесем все необходимые данные для расчета в наш проект. Именно, что нам понадобится, так это цена акции компании и годовая волатильность. Цена акции будет взять за 16 мая 2022 года (рисунок 3) []. 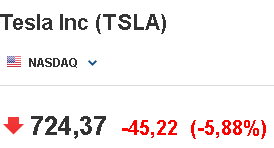 Рисунок 3 – цена акции "Tesla" Далее возьмем годовую волатильность ее можно увидеть на рисунке 4 []. Рисунок 4 – Годовая волатильность "Tesla" После сформулируем данные в нашем файле excel и запишем их туда (рисунок 5).  Рисунок 5 – Данные компании "Tesla" для имитационного моделирования Цена акции компании довольно изменчива и может изменяться ежедневно в отличии от нашей волатильности, которая меняется только раз в год. Но мы можем также рассчитать дневную волатильность, чтобы рассчитывать в будущем цену акции за каждый день, это и будет влиять на цену нашей акции в будущем, чтобы имитировать ее цену в ежедневном периоде времени. Для того, чтобы рассчитать дневную волатильность нам понадобится годовую волатильность разделить на корень из 252. Почему же 252? Так как периоды торговых дней составляют в среднем от 251 до 253 дней, мы возьмем его среднее значение 252. Мы получаем значение 3,45%, т.е. в среднем цена акции изменяется на 3,45% ежедневно в плюс или минус. 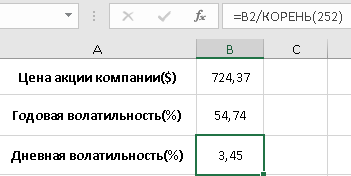 Рисунок 6 – Расчет дневной волатильности После того, как мы рассчитали наши значения, на нужно обратится к нашему генератору случайных чисел, чтобы смоделировать цену акции на любое количество дней в будущем, что мы и собираемся сделать. Рассчитаем для одного месяца торговых дней, их будет 21. Чтобы иметь представление о том, как они будут смоделированы. Наша таблица будет иметь следующий вид (рисунок 7).  Рисунок 7 – Таблица для симуляции цены акции Далее нам нужно рассчитать саму цену акции. Для начала рассчитаем цену для первого дня, формула расчета которого будет выглядеть следующим образом.  Рисунок 8 – Расчет цены акции первого торгового дня Первое, что мы делаем, так это ссылаемся на нашу начальную цену, которая равняется 724,37$. И умножаем ее на ожидаемую цену в течении дня, которая будет равно единице прибавленную к обратному нормированному распределению, который и будет нашим генератором случайных чисел. Работа функции НОРМ.ОБР() заключается следующим образом (рисунок 9).  Рисунок 9– Синтаксис и описание функции НОРМ.ОБР. В данную функцию мы записываем такие значения, как функцию СЛЧИС, которая будет генерировать случайное вещественное число от 0 до 1. В аргумент среднее мы подставляем 0, то есть мы говорим, что изменение цены будет равно 0 каждый день, а стандартным отклонением будет процент дневного волатильности. После всех расчетов мы и получаем случайное число и получается цена акции. Теперь, когда мы знаем цену нашей акции, мы можем рассчитать и цены за другие дни. А сделаем это следующим образом, теперь вместо данной нам цены акции мы будем брать цену за прошлый день, тем самым мы получим наши случайно сгенерированные числа (рисунок 10). 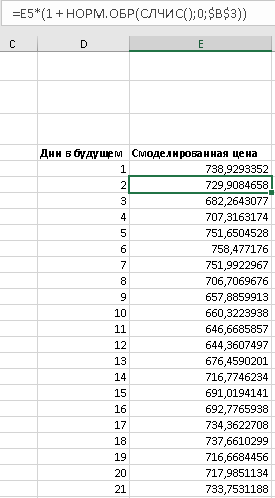 Рисунок 10 – Смоделированные цены акций за месяц торгов на бирже Мы также можем построить график, чтобы видеть полную динамику наших цен (рисунок 11). 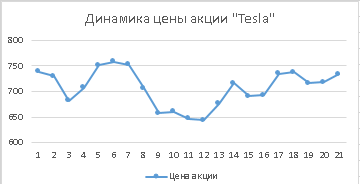 Рисунок 11 – График динамики цены акций в имитационной модели Но это еще не все, что нам нужно рассчитать, ведь мы смоделировали возврат один раз, а что, если нам понадобится смоделировать его несколько раз, к примеру 10. Мы возьмем результат 21 дня и сделаем диапазон значений к примеру, из 20 различных чисел, а после вычислим статистику по этим данным. Для этого сформируем следующую таблицу, куда запишем в столбик числа от 1 до 20, а в другой столбик будут выводится наши результаты.  Рисунок 12 – Таблица смоделированных событий конечного дня Теперь, как мы сформировали таблицу, нам нужно будет взять значение последнего дня в нашей прошлой таблице и сослаться на него в текущей таблице. В Excel выделяем наш диапазон двух столбцов, заходим во вкладку «Данные», после ищем закладку «Анализ “Что если?”» и нажимаем на «Таблицу данных». После где нам предлагают выбрать значения по строкам и ставим соседнею ячейку от последнего столбца. «Таблицы данных» обычно используются для проверки различных результатов модели. Так мы смогли смоделировать результат через каждый 21 день. Полученный результат можем увидеть на рисунке 13. 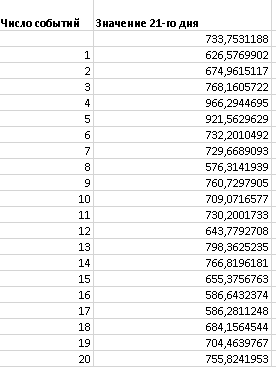 Рисунок 13 – Таблица моделируемых результатов значений через каждые 21 день После полученных нами значений, мы можем рассчитать статистику по этим данным и сделать некоторые выводы. Сперва рассчитаем среднее значение по полученным данным, для этого воспользуемся функцией СРЕДЗНАЧ. Данная функция рассчитывает среднее значение диапазона переданных в нее чисел (рисунок 14). 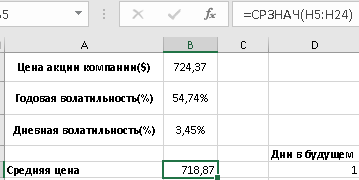 Рисунок 14 – Среднее значение полученных данных Мы получили значение 718,87$, то есть среднее значение цены всех наших акций, которые были в 21 день. Далее мы посчитаем медиану цены этих данных. Рассчитывать мы ее будем следующим образом. Воспользуемся функцией МЕДИАНА, которая поможет нам в этом, она принимаем диапазон чисел, где после рассчитывается сама медиана (рисунок 15). Медиана – это число, которое лежит в середине упорядоченного ряда чисел. 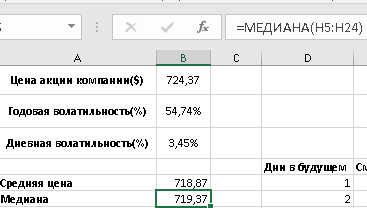 Рисунок 15 – Расчет медианы Проведя расчеты мы получаем, что медиана равна 719,37$. Так же есть возможность посчитать стандартное отклонение, которое рассчитывается также с помощью специальной функцией СТАНДОТКЛОН.В, которая принимает массив чисел (рисунок 16). 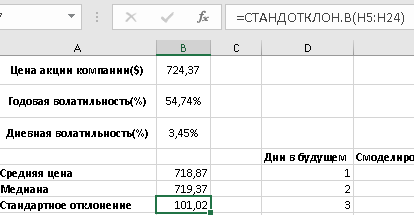 Рисунок 16 – Расчет стандартного отклонения Получаем, что наше стандартное отклонение равно 101,02. Стандартное отклонение – если говорить простыми словами, то это мера того, на сколько разбросаны данные в нашем диапазоне данных. Так же стоит рассчитать минимальное и максимальное значение в нашем диапазоне данных. Рассчитывать мы их будем с помощью специальных функций Excel: МИН() и МАКС(). Они принимают массив чисел, где высчитывается нужный нам результат. Получаются следующие результаты (рисунок 17). 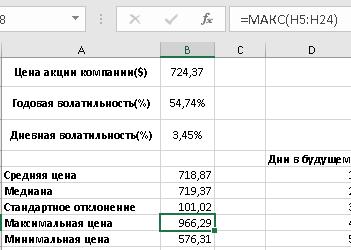 Рисунок 17 – Расчет минимального и максимального значения Мы получили, что максимальное значение в данном диапазоне 966,29$, а минимальное значение получилось 576,31$. Следующее, что можно рассчитать, так это процентиль. Процентиль – это определенная доля в выборке данных. Чтобы рассчитать процентиль нам также понадобится функция Excel, название данной функции выглядит следующим образом ПРОЦЕНТИЛЬ.ВКЛ. Функция имеет следующий синтаксис (рисунок 18).  Рисунок 18 – синтаксис функции ПРОЦЕНТИЛЬ.ВКЛ Посчитаем процентиль следующим образом и получим такие результаты, как показаны на рисунке 19. 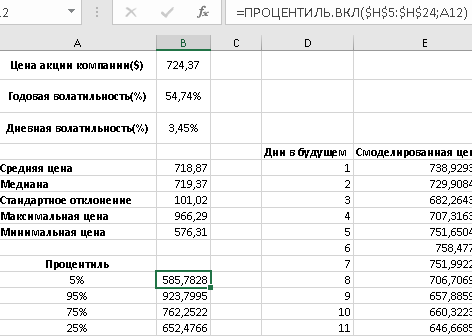 Рисунок 19 – Результаты процентиля и его расчет Так предположим, что акция наша равна пятому процентилю и ее цена будет 585,7828$, а для 95% будет равен 923,7995$, также рассчитаем для 75%, где результат будет равен 762,2522$, ну и для 25% результатом будет 652,4766%. На основе полученных данных мы можем сделать выводы и принять в последующем нужные решения. Когда мы решим применить данный метод, то стоит помнить, что речь идет об оценке общей устойчивости вашего проекта, к изменения факторов в нашем случае это цена акции и ее годовое и дневное изменение в процентах. Итоги всегда будут зависеть от полученных данных оценочных показателей, значения которых могут в последующие разы изменяться. ЗАКЛЮЧЕНИЕ В ходе данной курсовой работы мы рассмотрели такие темы, как модель и моделирование, еще мы дали понятие и все что связано с имитационным моделированием. Также мы исследовали метод Монте-Карло, рассмотрели его особенности при имитационном моделировании цены акций. Применили на практике данный метод воспользовавшись программными средствами Microsoft Excel. С практической точкой зрения данной работы были сделаны расчеты методом Монте-Карло, где было показано и доказано, что метод можно применять для решения множество задач из-за его адаптивности по сравнению с другими имитационными методами. Метод Монте-Карло применять можно практически во всех сферах жизнедеятельности и не только для имитации цены акций компании, но и в моделировании рисков или еще где-нибудь. На сегодняшний день существует множество программ для имитационного моделирования это MathLab, Excel и т.д. В заключении стоит сказать, что все в нашей жизни можно представить в виде модели, можно рассчитать с ее помощью все что угодно, а метод Монте-Карло можно применить практически везде, и чтобы его понять не нужно быть специалистом высокого уровня метод прост и понятен каждому. Список используемых источников1 2 |
