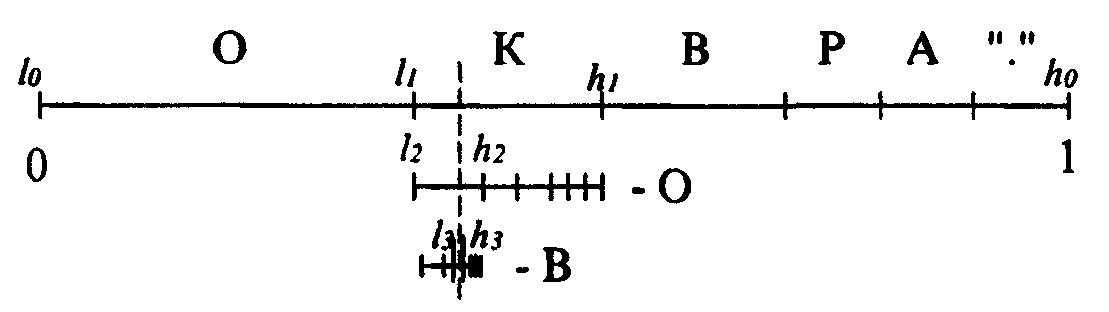курсовая6. Курсовая работа Кредитный рынок и его место в системе макроэкономического кругооборота

• Название: Курсовая работа Кредитный рынок и его место в системе макроэкономического кругооборота
• Дата: 14.05.2019
• Размер: 340.59 Kb.
• Имя файла: курсовая6.docx
• Тип: Курсовая; #76997
• страница: 2 из 7

Обзор алгоритмов:

В настоящее время существует несколько алгоритмов сжатия без потерь, частично это открытые алгоритмы, частично коммерческие алгоритмы. Открытые алгоритмы обычно рассматривают только саму идею, не останавливаясь на проблемах ее реализации в виде программы или реализованы в виде «демонстрационной» (не очень эффективной) программы. Коммерческий алгоритм обычно включает в себя не только идею алгоритма сжатия, но и эффективную реализацию алгоритма в виде программы. Коммерческие алгоритмы не публикуются и познакомится с ними невозможно, за исключением ознакомления с результатами работы программ на базе этих алгоритмов. Соответствующие программы (ZIP, ARJ, RAR, ACE и др.) достаточно известны и с ними можно познакомиться самостоятельно.

Алгоритмы обратимого сжатия данных можно разделить на две группы:

• 
  1) Алгоритмы частотного анализа для подсчета частоты различных символов в данных и преобразование кодов символов с соответствии с их частотой.
  
• 
  2) Алгоритмы корреляционного анализа для поиска корреляций (в простейшем случае точных повторов) между различными участками данных и замена коррелирующих данных на код(ы), позволяющая восстановить данные на основе предшествующих данных. В простейшем случае точных повторов, кодом является ссылка на начало предыдущего вхождения этой последовательности символов в данных и длина последовательности.
  

Можно отметить следующие алгоритмы обратимого сжатия данных из первой группы:

• 
  1) Метод Хаффмана - замена кода равной длины для символов на коды неравной длины в соответствии с частотой появления символов в данных. Коды минимальной длины присваиваются наиболее часто встречающимся символам. Если частоты появления символов являются степенью двойки (2ⁿ), то этот метод достигает теоретической энтропийной границы эффективности сжатия для методов такого типа.
  
• 
  2) Метод Шеннона-Фано - сходен с методом Хаффмана, но использует другой алгоритм генерации кодов и не всегда дает оптимальные коды (оптимальный код - код дающий наибольшее сжатие данных из всех возможных для данного типа преобразования).
  
• 
  3) Арифметическое кодирование - усовершенствование метода Хаффмана, позволяющее получать оптимальные коды для данных, где частоты появления символов не являются степенью двойки (2ⁿ). Этот метод достигает теоретической энтропийной границы эффективности сжатия этого типа для любого источника.
  

Для второй группы можно назвать следующие алгоритмы :

• 
  1) Метод Running (или RLE) - заменяет цепочки повторяющихся символов на код символа и число повторов. Это пример элементарного и очень понятного метода сжатия, но, к сожалению, он не обладает достаточной эффективностью.
  
• 
  2) Методы Лемпеля-Зива - это группа алгоритмов сжатия объединенная общей идеей: поиск повторов фрагментов текста в данных и замена повторов ссылкой (кодом) на первое (или предыдущее) вхождение этого фрагмента в данные. Отличаются друг от друга методом поиска фрагментов и методом генерации ссылок(кодов).
  

В настоящее время, в различных модификациях и сочетаниях, два алгоритма-метод Хаффмана (или арифметическое кодирование) и метод Лемпеля-Зива-составляют основу всех коммерческих алгоритмов и программ.

Далее будут подробно рассмотрены несколько вариантов алгоритма сжатия.

2.2. По алгоритму Хаффмана

Этот алгоритм кодирования информации был предложен Д.А. Хаффманом в 1952 году. Идея алгоритма состоит в следующем: зная вероятности вхождения символов в сообщение, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью присваиваются более короткие коды. Коды Хаффмана имеют уникальный префикс, что и позволяет однозначно их декодировать, несмотря на их переменную длину.

Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево). Алгоритм построения Н-дерева прост и элегантен.

1. Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.

2. Выбираются два свободных узла дерева с наименьшими весами.

3. Создается их родитель с весом, равным их суммарному весу.

4. Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка.

5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой - бит 0.

6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.

Допустим, у нас есть следующая таблица частот:

15	7	6	6	5
А	Б	В	Г	Д

На первом шаге из листьев дерева выбираются два с наименьшими весами — Г и Д. Они присоединяются к новому узлу-родителю, вес которого устанавливается в 5+6 = 11. Затем узлы Г и Д удаляются из списка свободных. Узел Г соответствует ветви 0 родителя, узел Д — ветви 1.

На следующем шаге то же происходит с узлами Б и В, так как теперь эта пара имеет самый меньший вес в дереве. Создается новый узел с весом 13, а узлы Б и В удаляются из списка свободных. После всего этого дерево кодирования выглядит так, как показано на рис. 2.


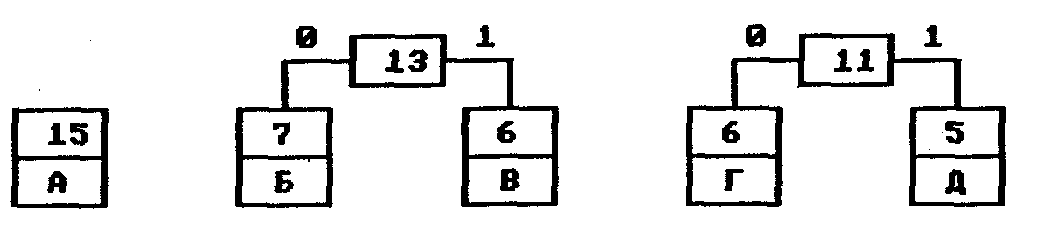
Рис. 2. Дерево кодирования Хаффмана после второго шага
На следующем шаге «наилегчайшей» парой оказываются узлы Б/В и Г/Д. Для них еще раз создается родитель, теперь уже с весом 24. Узел Б/В соответствует ветви 0 родителя, Г/Д—ветви 1.

На последнем шаге в списке свободных осталось только два узла — это А и узел (Б/В)/(Г/Д). В очередной раз создается родитель с весом 39 и бывшие свободными узлы присоединяются к разным его ветвям.

Поскольку свободным остался только один узел, то алгоритм построения дерева кодирования Хаффмана завершается.
Н-дерево представлено на рис. 3.


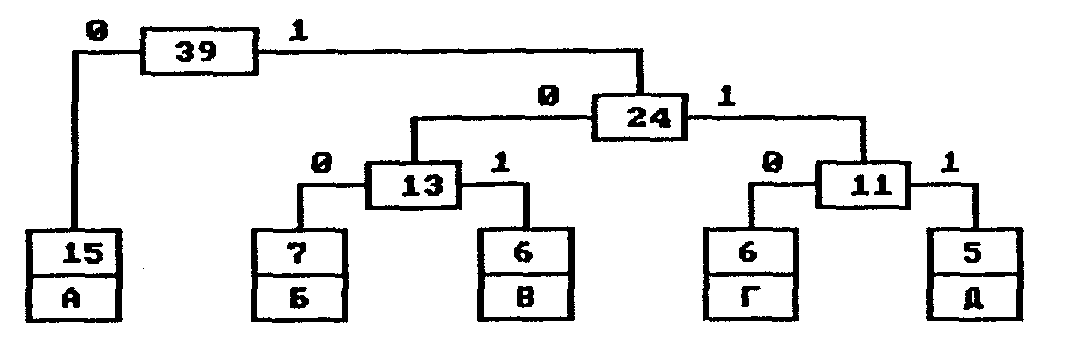
Рис. 3. Окончательное дерево кодирования Хаффмана

Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от листа дерева, соответствующего этому символу, до корня дерева, накапливая биты при перемещении по ветвям дерева. Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.

Дня данной таблицы символов коды Хаффмана будут выглядеть следующим образом.

А 0

Б 100

В 101

Г 110

Д 111

Поскольку ни один из полученных кодов не является префиксом другого, они могут быть однозначно декодированы при чтений их из потока. Кроме того, наиболее частый символ сообщения А закодирован наименьшим количеством битов, а наиболее редкий символ Д - наибольшим.

Классический алгоритм Хаффмана имеет один существенный недостаток. Дня восстановления содержимого сжатого сообщения декодер должен знать таблицу частот, которой пользовался кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию сообщения. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по сообщению: одного для построения модели сообщения (таблицы частот и Н-дерева), другого для собственно кодирования.


2.3 По алгоритму Шеннона-Фано
Кодирование Шеннона-Фано является одним из самых первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон (Shannon) и Фано (Fano). Данный метод сжатия имеет большое сходство с кодированием Хаффмана, которое появилось на несколько лет позже. Главная идея этого метода - заменить часто встречающиеся символы более короткими кодами, а редко встречающиеся последовательности более длинными кодами. Таким образом, алгоритм основывается на кодах переменной длины. Для того, чтобы декомпрессор впоследствии смог раскодировать сжатую последовательность, коды Шеннона-Фано должны обладать уникальностью, то есть, не смотря на их переменную длину, каждый код уникально определяет один закодированый символ и не является префиксом любого другого кода.
   Рассмотрим алгоритм вычисления кодов Шеннона-Фано (для наглядности возьмём в качестве примера последовательность 'aa bbb cccc ddddd'). Для вычисления кодов, необходимо создать таблицу уникальных символов сообщения c(i) и их вероятностей p(c(i)), и отсортировать

ее в порядке невозрастания вероятности символов.

c(i)	p(c(i))
d	5 / 17
c	4 / 17
space	3 / 17
b	3 / 17
a	2 / 17

 Далее, таблица символов делится на две группы таким образом, чтобы каждая из групп имела приблизительно одинаковую частоту по сумме символов. Первой группе устанавливается начало кода в '0', второй в '1'. Для вычисления следующих бит кодов символов, данная процедура повторяется рекурсивно для каждой группы, в которой больше одного символа. Таким образом для нашего случая получаем следующие коды символов:

символ	код
d	00
c	01
space	10
b	110
a	111

   Длина кода s(i) в полученной таблице равна int(-lg p(c(i))), если сиволы удалость разделить на группы с одинаковой частотой, в противном случае, длина кода равна int(-lgp(c(i)))+1. 

int(-lg p(c(i))) <= s(i) <= int(-lg p(c(i))) + 1

   Успользуя полученную таблицу кодов, кодируем входной поток - заменяем каждый символ соответствующим кодом. Естественно для расжатия полученной последовательности, данную таблицу необходимо сохранять вместе со сжатым потоком, что является одним из недостатков данного метода. В сжатом виде, наша последовательность принимает вид:

111111101101101101001010101100000000000

длиной в 39 бит. Учитывая, что оргинал имел длину равную 136 бит, получаем коэффициент сжатия 28% - не так уж и плохо.
   Глядя на полученную последовательность, возникает вопрос: "А как же теперь это расжать ?". Мы не можем, как в случае кодирования, заменять каждые 8 бит входного потока, кодом переменной длины. При расжатии нам необходимо всё сделать наоборот - заменить код переменной длины символом длиной 8 бит. В данном случае, лучше всего будет использовать бинарное дерево, листьями которого будут являтся символы (аналогдерева Хаффмана).
   Кодирование Шеннона-Фано является достаточно старым методом сжатия , и на сегодняшний день оно не представляет особого практического интереса (разве что как упражнение по курсу структур данных). В большинстве случаев, длина сжатой последовательности, по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях всё же формируются не оптимальные коды Шеннона-Фано, поэтому сжатие методом Хаффмана принято считать более эффективным. Для примера, рассмотрим последовательность с таким содержанием символов: 'a' - 14, 'b' - 7, 'c' - 5, 'd' - 5, 'e' - 4. Метод Хаффмана сжимает её до 77 бит, а вот Шеннона-Фано до 79 бит.

символ код Хаффмана код Шеннона-Фано a 0 00 b 111 01 c 101 10 d 110 110 e 100 111

 

  Кстати, в одном источнике (не буду указывать каком), эту последовательность сжали методом Шеннона-Фано до 84 бит, а методом Хаффмана до тех же 77. Такие отличаи в степени сжатия возникают из-за нестрогого определения способа деления символов на группы.
   Как же мы делили на группы ? Достаточно просто:

вероятноть первой группы (p1)и второй (p2) равна нулю; p1 <= p2 ? да: добавить в первую группу символ с начала таблицы; нет: добавить во вторую группу символ с конца таблицы; если все символы разделены на группы, то завершить алгоритм, иначе перейти к шагу 2. Из-за такой неопределённости у некоторых людей возникают даже такие мысли: "... программа иногда назначает некоторым символам ..." и так далее - рассуждения о длине кодов. Если вы не пишете AI, то такое понятие, как "программа иногда" что-то делает, звучит смешно. Правильно реализованный алгоритм - работает строго опеределённо.

2.4 Алгоритм арифметического кодирования

Арифметическое сжатие - достаточно изящный метод, в основе которого лежит очень простая идея. Мы представляем кодируемый текст в виде дроби, при этом строим дробь таким образом, чтобы наш текст был представлен как можно компактнее. Для примера рассмотрим построение такой дроби на интервале [0, 1) (0 - включается, 1 - нет). Интервал [0, 1) выбран потому, что он удобен для объяснений. Мы разбиваем его на подынтервалы с длинами, равными вероятностям появления символов в потоке. В дальнейшем будем называть их диапазонами соответствующих символов.

Пусть мы сжимаем текст "КОВ.КОРОВА" (что, очевидно, означает "коварная корова"). Распишем вероятности появления каждого символа в тексте (в порядке убывания) и соответствующие этим символам диапазоны:

Символ	Частота	Вероятность	Диапазон
О	3	0.3	[0.0; 0.3)
К	2	0.2	[0.3; 0.5)
В	2	0.2	[0.5; 0.7)
Р	1	0.1	[0.7; 0.8)
А	1	0.1	[0.8; 0.9)
“.”	1	0.1	[0.9; 1.0)

Будем считать, что эта таблица известна в компрессоре и декомпрессоре. Кодирование заключается в уменьшении рабочего интервала. Для первого символа в качестве рабочего интервала берется [0, 1). Мы разбиваем его на диапазоны в соответствии с заданными частотами символов (см. таблицу диапазонов). В качестве следующего рабочего интервала берется диапазон, соответствующий текущему кодируемому символу. Его длина пропорциональна вероятности появления этого символа в потоке. Далее считываем следующий символ. В качестве исходного берем рабочий интервал, полученный на предыдущем шаге, и опять разбиваем его в соответствии с таблицей диапазонов. Длина рабочего интервала уменьшается пропорционально вероятности текущего символа, а точка начала сдвигается вправо пропорционально началу диапазона для этого символа. Новый построенный диапазон берется в качестве рабочего и т. д.

Используя исходную таблицу диапазонов, кодируем текст "КОВ.КОРОВА":

Исходный рабочий интервал [0,1).

Символ "К" [0.3; 0.5) получаем [0.3000; 0.5000).

Символ "О" [0.0; 0.3) получаем [0.3000; 0.3600).

Символ "В" [0.5; 0.7) получаем [0.3300; 0.3420).

Символ "." [0.9; 1.0) получаем [0,3408; 0.3420).

Графический процесс кодирования первых трех символов можно представить так, как на рис. 4.


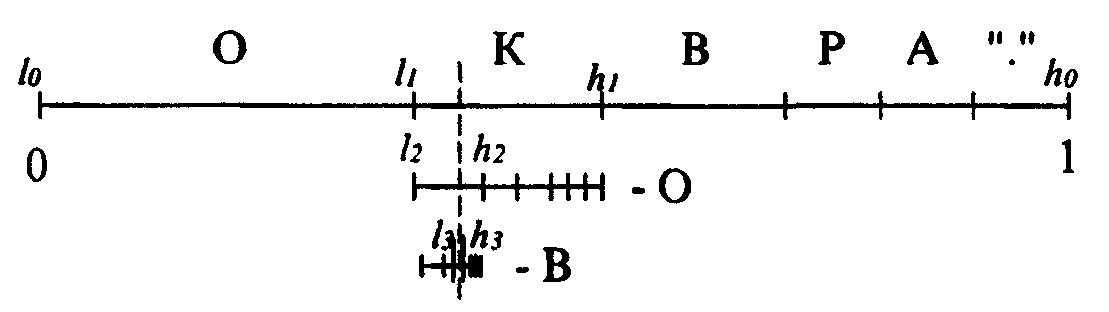
Рис. 4. Графический процесс кодирования первых трех символов
Таким образом, окончательная длина интервала равна произведению вероятностей всех встретившихся символов, а его начало зависит от порядка следования символов в потоке. Можно обозначить диапазон символа с как [а[с]; b[с]), а интервал для i-го кодируемого символа потока как [l_i, h_i).

Большой вертикальной чертой на рисунке выше обозначено произвольное число, лежащее в полученном при работе интервале [/_i, h_i). Для последовательности "КОВ.", состоящей из четырех символов, за такое число можно взять 0.341. Этого числа достаточно для восстановления исходной цепочки, если известна исходная таблица диапазонов и длина цепочки.

Рассмотрим работу алгоритма восстановления цепочки. Каждый следующий интервал вложен в предыдущий. Это означает, что если есть число 0.341, то первым символом в цепочке может быть только "К", поскольку только его диапазон включает это число. В качестве интервала берется диапазон "К" - [0.3; 0.5) и в нем находится диапазон [а[с]; b[с]), включающий 0.341. Перебором всех возможных символов по приведенной выше таблице находим, что только интервал [0.3; 0.36), соответствующий диапазону для "О", включает число 0.341. Этот интервал выбирается в качестве следующего рабочего и т. д.