Алгоритмы и структуры данных. Деревья. Алгоритмы и структуры данных. Курсовая работа по дисциплине Алгоритмы и структуры данных Использование алгоритмов обработки данных при разработке приложений
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
 Министерство науки и высшего образования Российской Федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Факультет математики и информационных технологий Кафедра программного обеспечения вычислительной техники и автоматизированных систем КУРСОВАЯ РАБОТА по дисциплине «Алгоритмы и структуры данных» Использование алгоритмов обработки данных при разработке приложений Пояснительная записка ОГУ 09.03.04.3021.780 ПЗ
Оренбург 2021 Утверждаю заведующий кафедрой программного обеспечения вычислительной техники и автоматизированных систем _____________________Н.А. Соловьев подпись «____»______________________2021 г. ЗАДАНИЕ на выполнение курсовой работы студенту Жукову Дмитрию Сергеевичу (фамилия имя отчество) по направлению подготовки 09.03.04 Программная инженерия код, наименование по дисциплине «Алгоритмы и структуры данных» наименование дисциплины, модуля 1 Тема работы «Использование алгоритмов обработки данных при разработке приложений» 2 Срок сдачи студентом работы «____»_________________20___ г. 3 Цель и задачи работы овладение навыками использования структур данных и алгоритмов обработки данных при разработке приложений; закрепление знаний и развитие практических навыков разработки программных средств. 4 Исходные данные к работе Вариант №25. Разработать программу, реализующую алгоритм Дейкстры для определения кратчайшего пути в графе. Программа должна позволять пользователю задавать граф в графическом режиме, а также наглядно отображать результат выполнения алгоритма. 5 Перечень вопросов, подлежащих разработке 1) анализ структур данных и алгоритмов их обработки; 2) разработка алгоритмов программного средства; 3) выбор языка программирования; 4) программная реализация структур данных; 5) тестирование программного средства. Дата выдачи и получения задания Руководитель «____»______________20__ г. ______________С.А. Климачев Студент «____»______________20__ г. ________________Д.С. Жуков Аннотация Курсовая работа посвящена вопросу поиска наикратчайшего пути в графе без ребер отрицательного веса. В работе рассматривается поиск наикратчайшего пути в графах на основе алгоритма Дейкстра. Описано нахождение кратчайшего расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. А так же показан процесс поиска графически в разработанной программе. Пояснительная записка к курсовой работе содержит 22 листа, 12 рисунок, 10 информационных источников, 1 приложение. Содержание Введение 5 1 Анализ структур данных и алгоритмов их обработки 7 2 Разработка алгоритмов программного средства 12 3 Выбор языка программирования 14 4 Программная реализация структур данных 16 5 Тестирование программного средства 17 Заключение 18 Список использованных источников 19 Приложение А Код программы 20 Введение При взгляде на географическую карту сразу бросается в глаза сеть железных дорог, что является типичным графом. Рассмотрим классическую задачу о коммивояжере. Существует много различных маршрутов поездки. А выбрать из них наикратчайший поможет граф. Графы используются в строительстве при планировании проведения работ; для решения логических проблем, связанных с перебором вариантов и во многих других вопросах. Впервые основы теории графов появились в работе Л.Эйлера, где он описывал решения головоломок и математических развлекательных задач. Широкое же развитие теория графов получила лишь в 50-х годах ХХ века в связи со становлением кибернетики и развитием вычислительной техники. В программировании логика незаменима как строгий язык и служит для описания сложных утверждений, значение которых может определить компьютер. Целью курсовой работы является закрепление знаний по дисциплине «Структуры и алгоритмы обработки данных», практическое овладение математическим аппаратом, характерным для современной теории анализа сложных систем (теории графов). Благодаря своему широкому применению, теория о нахождении кратчайших путей в последнее время интенсивно развивается.Нахождение кратчайшего пути – жизненно необходимо и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (например, кратчайший путь от дома до университета), в системах автопилота, для нахождения оптимального маршрута при перевозках, коммутации информационного пакета в Internet и т.п. Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Компьютерные средства и информационные технологии повысили возможности такого всеохватывающего метода изучения и создания, как моделирования объектов, явлений и процессов – как тех, что существуют в природе, так и тех, что создаются человеком искусственно. Количество объектов усложнялись, увеличивались, и натурное моделирование (макеты сооружений) стало невыгодным, неэкономным. Поэтому для изучения начали применять математику. Использование математических моделей – уравнения, неравенства, формулы и тому подобное называется математическим моделированием, для развития и приспособления которого нужны были эффективные численные методы. Реализовать большой потенциал математического моделирования невозможно без мощных средств автоматизации вычислений, которыми являются компьютеры. Благодаря появлению компьютеров и развитию информационных технологий создаются методы и средства компьютерного моделирования, способные решать сложные практические задачи, такие как управление большими энергетическими системами, создание достоверных прогнозов погоды или урожая, моделирование региональных и общегосударственных систем, проектирование самолетов, кораблей и т. п. Компьютерная модель – это размещенная в компьютере совокупность средств, что реализуют концепцию вычисления. Для реализации компьютерной модели, большое значение имеет такое научное направление, как программирование. Без него компьютер это просто набор различных устройств, микросхем, который не может быть полезным.Из всех объектно-ориентированных языков С++ является наиболее широко используемым. И именно с его помощью в данном курсовом проекте реализуется алгоритм Дейкстра. 1 Анализ структур данных и алгоритмов их обработкиАлгоритм находит все кратчайшие пути из одной изначально заданной вершины графа до всех остальных. С его помощью, при наличии всей необходимой информации, можно, например, узнать какую последовательность дорог лучше использовать, чтобы добраться из одного города до каждого из многих других, или в какие страны выгодней экспортировать нефть и тому подобное. Минусом данного метода является невозможность обработки графов, в которых имеются ребра с отрицательным весом. На конкретном графе проследим работу алгоритма, найдем все кратчайшие пути между истоковой и всеми остальными вершинами. Размер (количество ребер) изображенного ниже графа равен 7 (|E|=7), а порядок (количество вершин) – 6 (|V|=6). Это взвешенный граф, каждому из его ребер поставлено в соответствие некоторое числовое значение, поэтому ценность маршрута необязательно определяется числом ребер, лежащих между парой вершин (рисунок 1). Р 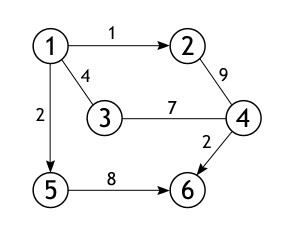 исунок 1 – Исходный граф Из всех вершин входящих во множество V выберем одну, ту, от которой необходимо найти кратчайшие пути до остальных доступных вершин. Пусть таковой будет вершина 1. Длина пути до всех вершин, кроме первой, изначально равна бесконечности, а до нее – 0, т. к. граф не имеет петель (рисунок 2). Р 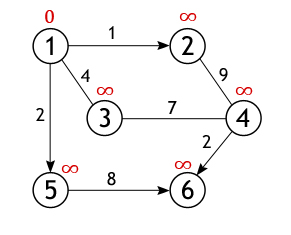 исунок 2 – Выбранная вершина 1 У вершины 1 ровно 3 соседа (вершины 2, 3, 5), и чтобы вычислить длину пути до них нужно сложить вес дуг, лежащих между вершинами: 1 и 2, 1 и 3, 1 и 5 со значением первой вершины. Получившиеся значения присваиваются вершинам, лишь в том случае если они «лучше» (меньше) тех которые значатся на настоящий момент. А так как каждое из трех чисел меньше бесконечности, они становятся новыми величинами, определяющими длину пути из вершины 1 до вершин 2, 3 и 5 (рисунок 3). Далее, активная вершина помечается как посещенная, статус «активной» переходит к одной из ее соседок, а именно к вершине 2, поскольку она ближайшая к ранее активной вершине. У вершины 2 всего один не рассмотренный сосед (вершина 1 помечена как посещенная), расстояние до которого из нее равно 9, но нам необходимо вычислить длину пути из истоковой вершины, для чего нужно сложить величину приписанную вершине 2 с весом дуги из нее в вершину 4 (рисунок 4). 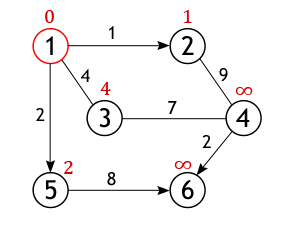 Рисунок 3 – Длина пути из вершины 1 до вершин 2, 3 и 5 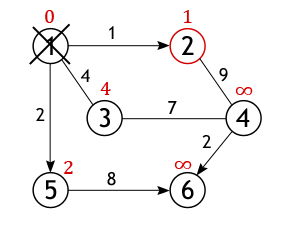 Рисунок 4 – Посещенная вершина 1 Условие «краткости» (10<∞) выполняется, следовательно, вершина 4 получает новое значение длины пути (рисунок 5). 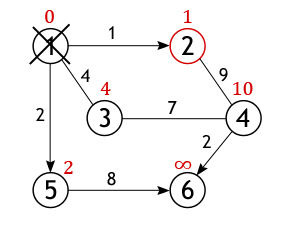 Рисунок 5 – Вершина 4 получает новое значение длины пути Вершина 2 перестает быть активной, также как и вершина 1 удаляется из списка не посещённых. Теперь тем же способом исследуются соседи вершины 5, и вычисляется расстояние до них (рисунок 6). 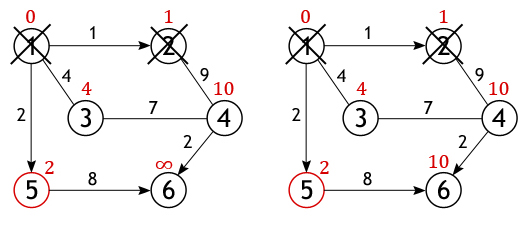 Рисунок 6 – Вершина 1 удаляется, исследуются соседние вершины и вычисляется расстояние до них Когда дело доходит до осмотра соседей вершины 3, то тут важно не ошибиться, т. к. вершина 4 уже была исследована и расстояние одного из возможных путей из истока до нее вычислено. Если двигаться в нее через вершину 3, то путь составит 4+7=11, а 11>10, поэтому новое значение игнорируется, старое остается (рисунок 7). 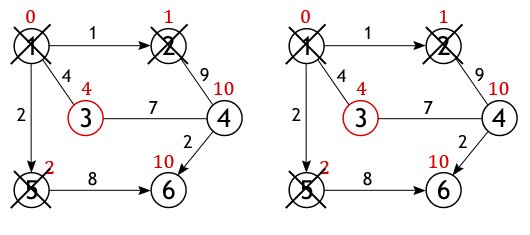 Рисунок 7 – Продолжение поиска пути Аналогичная ситуация с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно получается только в том случае, если идти через вершину 5. Когда все вершины графа, либо все те, что доступны из истока, будут помечены как посещенные, тогда работа алгоритма Дейкстры завершится, и все найденные пути будут кратчайшими (рисунок 8).  Рисунок 8 – Конечный результат В программе, находящей ближайшие пути между вершинами посредством метода Дейкстры, граф будет представлен в виде не бинарной матрицы смежности. Вместо единиц в ней будут выставлены веса ребер, функция нулей останется прежней: показывать, между какими вершинами нет ребер или же они есть, но отрицательно направленны. 2 Разработка алгоритмов программного средства Для программной реализации алгоритма понадобиться два массива: логический visited – для хранения информации о посещенных вершинах и численный distance, в который будут заноситься найденные кратчайшие пути. Итак, имеется графG=(V, E). Каждая из вершин входящих во множество V, изначально отмечена как не посещенная, т. е. элементам массива visited присвоено значениеfalse. Поскольку самые выгодные пути только предстоит найти, в каждый элемент вектора distance записывается такое число, которое заведомо больше любого потенциального пути (обычно это число называют бесконечностью, но в программе используют, например максимальное значение конкретного типа данных). В качестве исходного пункта выбирается вершина s и ей приписывается нулевой путь: distance[s]=0, т. к. нет ребра из s в s (метод не предусматривает петель). Далее, находятся все соседние вершины (в которые есть ребро из s) [пусть таковыми будут t и u и поочередно исследуются, а именно вычисляется стоимость маршрута из s поочередно в каждую из них: distance[t]=distance[s]+весинцидентного s и t ребра; distance[u]=distance[s]+ весинцидентного s и u ребра. Но вполне вероятно, что в ту или иную вершину из s существует несколько путей, поэтому цену пути в такую вершину в массиве distance придется пересматривать, тогда наибольшее (неоптимальное) значение игнорируется, а наименьшее ставиться в соответствие вершине. После обработки смежных с s вершин она помечается как посещенная: visited[s]=true, и активной становится та вершина, путь из s в которую минимален. Допустим, путь из s в u короче, чем из s в t, следовательно, вершина u становиться активной и выше описанным образом исследуются ее соседи, за исключением вершины s. Далее, u помечается как пройденная: visited[u]=true, активной становится вершина t, и вся процедура повторяется для нее. Алгоритм Дейкстры продолжается до тех пор, пока все доступные из s вершины не будут исследованы. Более подробно алгоритм описан в приведенной ниже блок-схеме (рисунок 9).  Рисунок 9 – Блок-схема алгоритма Дейкстры 3 Выбор языка программирования В данной работе при программной реализации алгоритма Дейкстры были рассмотрены языки программирования С++, Python, Delphi. Каждый язык программирования имеет свои преимущества. Рассмотрим каждый язык программирования подробнее. Язык программирования С++ поддерживает такие парадигмы программирования, как процедурное программирование, объектно-ориентированное программирование, обобщённое программирование. Язык имеет богатую стандартную библиотеку, которая включает в себя распространённые контейнеры и алгоритмы, ввод-вывод, регулярные выражения, поддержку многопоточности и другие возможности. C++ сочетает свойства как высокоуровневых, так и низкоуровневых языков. В сравнении с его предшественником — языком C — наибольшее внимание уделено поддержке объектно-ориентированного и обобщённого программирования. Язык программирования C++ широко используется для разработки программного обеспечения, являясь одним из самых популярных языков программирования. Область его применения включает создание операционных систем, разнообразных прикладных программ, драйверов устройств, приложений для встраиваемых систем, высокопроизводительных серверов, а также игр. Существует множество реализаций языка C++, как бесплатных, так и коммерческих и для различных платформ. Например, на платформе x86 это GCC, Visual C++, Intel C++ Compiler, Embarcadero (Borland) C++ Builder и другие. C++ оказал огромное влияние на другие языки программирования, в первую очередь на Java и C#. Язык программирования Python это высокоуровневый язык программирования общего назначения с динамической строгой типизацией и автоматическим управлением памятью, ориентированный на повышение производительности разработчика, читаемости кода и его качества, а также на обеспечение переносимости написанных на нём программ. Язык является полностью объектно-ориентированным — всё является объектами. Необычной особенностью языка является выделение блоков кода пробельными отступами. Синтаксис ядра языка минималистичен, за счёт чего на практике редко возникает необходимость обращаться к документации. Сам же язык известен как интерпретируемый и используется в том числе для написания скриптов. Недостатками языка являются зачастую более низкая скорость работы и более высокое потребление памяти написанных на нём программ по сравнению с аналогичным кодом, написанным на компилируемых языках, таких как Си или C++. Язык программирования Делфи это императивный, структурированный, объектно-ориентированный, высокоуровневый язык программирования со строгой статической типизацией переменных. Основная область использования — написание прикладного программного обеспечения. Этот язык программирования является диалектом языка Object Pascal. При создании языка (и здесь качественное отличие от языка C) не ставилось задачи обеспечить максимальную производительность исполняемого кода или лаконичность исходного кода для экономии оперативной памяти. Изначально язык ставил во главу угла стройность и высокую читаемость, поскольку был предназначен для обучения дисциплине программирования. Эта изначальная стройность в дальнейшем, как по мере роста аппаратных мощностей, так и в результате появления новых парадигм, упростила расширение языка новыми конструкциями. Так, сложность объектного C++, по сравнению с C, выросла весьма существенно и затруднила его изучение в качестве первого языка программирования, чего нельзя сказать об Object Pascal относительно Pascal. После рассмотрения предложенных языков программирования в данной работе будет использоваться язык программирования Делфи так он прост для написания программ. 4 Программная реализация структур данных6 Тестирование программного средства  Рисунок 10 – Заполнение вершин графа  Рисунок 11 – Ввод начальной вершины |