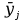курсовая. курсач. Курсовая работа по дисциплине Аналитические и численные методы в планировании экспериментов и инженерном анализе
 Скачать 38.03 Kb. Скачать 38.03 Kb.
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Чувашский государственной аграрный университет» (ФГБОУ ВО Чувашской ГАУ) Инженерный институт Курсовая работа по дисциплине «Аналитические и численные методы в планировании экспериментов и инженерном анализе» Выполнил студент 1 курса инженерного факультета заочной формы обучения, обучающего по направлению подготовки «ЭТ-1МЗ» Шифр: Проверил Чебоксары – 2021 г. Задание на курсовую работу Вариант №1 1. В соответствии с вариантом (таблица 1) спланировать факторный эксперимент ПФЭ 23. 2. Найти значения коэффициентов регрессии вида 𝑦 = 𝑏0 + 𝑏1𝑥1 + 𝑏2𝑥2 + 𝑏3𝑥3 + 𝑏12𝑥1𝑥2 + 𝑏13𝑥1𝑥3 + 𝑏23𝑥2𝑥3 + 𝑏123𝑥1𝑥2𝑥3. 3. Определить средние значения исследуемого параметра для каждой точки факторного пространства. 4. Определить дисперсии исследуемого параметра в каждой точке факторного пространства. 5. Проверить гипотезу однородности дисперсий по критерию Кохрена. 6. Проверить значимость коэффициентов регрессии. 7. Исключить незначимые коэффициенты регрессии. 8. Записать окончательный вид уравнения регрессии. 9. Проверить адекватность полученной математической модели. 10. Анализировать результаты исследований.
Оглавление Введение…………………………………………………………...………………4 1. Спланируем факторный эксперимент ПФЭ 23 в соответствии с вариантом ……………………………………..……………………………………...….…….6 2. Определим средние значения исследуемого параметра для каждой точки факторного пространства…………………………………………………...…….6 3. Определим дисперсии исследуемого параметра в каждой точке факторного пространства……………………………………………………………………....7 4. Проверим гипотезу однородности дисперсий по критерию Кохрена….......7 5. Расчет оценок коэффициентов уравнения регрессии………......……………8 6. Проверим значимость коэффициентов модели………………………………9 7. Проверим адекватность полученной модели…...…………………………...10 8. Список использованной литературы………………………………………...13 Введение Эксперимент является основным и наиболее совершенным методом познания. Он может быть активным и пассивным. Осуществление пассивного эксперимента не зависит от экспериментатора, и ему приходится довольствоваться лишь ролью наблюдателя. Основной вид эксперимента – активный, проводится в контролируемых и управляемых условиях. Все факторы, влияющие на исследуемые параметры объекта, предусмотреть, как правило, не удается. Так, в сложных системах, зависящих от множества факторов, некоторые воздействия не могут контролироваться или управляться. Воздействие этих факторов рассматриваются как белый шум, наложенный на истинные результаты эксперимента. Чтобы отделить факторы, интересующие экспериментатора, от шумового фона, применяются специальные методы, называемые рандомизацией эксперимента. Проведение активного эксперимента зачастую требует больших материальных затрат. Поэтому важной задачей является получение необходимых сведений при минимальном числе опытов. Решением этой проблемы занимается теория планирования эксперимента, представляющая собой раздел математической статистики. В общем случае она позволяет ответить на вопросы: - как спланировать эксперимент, обеспечивающий при требуемой точности результатов, минимальные затраты времени и средств; - как обработать результаты, чтобы извлечь из них максимум информации об исследуемом объекте; - какие выводы можно сделать по результатам эксперимента и какова достоверность этих выводов. Активный эксперимент в сочетании с методами планирования позволяет получить требуемые результаты, затратив минимальные средства и время на проведение исследования. Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения с требуемой точностью и достоверностью поставленной задачи. Целью планирования эксперимента, как правило, является получение математической модели (ММ) исследуемого объекта или процесса. Если на объект действует много факторов, механизм которых не известен, то обычно используют полиномиальные ММ (алгебраические полиномы), называемые уравнениями регрессии. Таблица 1.
1. Спланируем факторный эксперимент ПФЭ 23 в соответствии с вариантом табл.1 Таблица 2.
2. Определим средние значения исследуемого параметра для каждой точки факторного пространства:
ȳ1 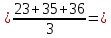 31,33; 31,33;ȳ2 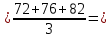 76,67; 76,67;ȳ3 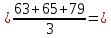 69; 69;ȳ4 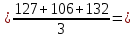 121,67; 121,67;ȳ5 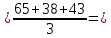 48,67; 48,67;ȳ6 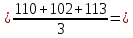 108,33; 108,33;ȳ7 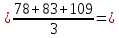 90; 90;ȳ8 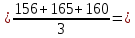 160,33. 160,33.Занесём полученные данные в табл.2. 3. Определим дисперсии исследуемого параметра в каждой точке факторного пространства:
 = 52,34; = 52,34;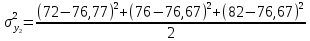 = 25,34; = 25,34;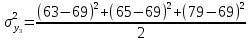 = 76; = 76;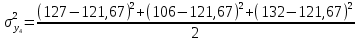 = 190,34; = 190,34;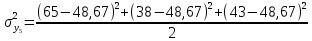 = 206,34; = 206,34;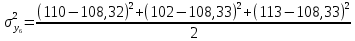 = 32,34; = 32,34;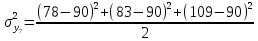 = 277; = 277; = 20,37. = 20,37.4. Проверим гипотезу однородности дисперсий по критерию Кохрена:
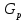 = = 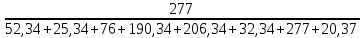 = 0,31. = 0,31.Опыт считается воспроизводимым, если дисперсия 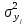 выходного параметра выходного параметра  однородна в каждой точке факторного пространства. однородна в каждой точке факторного пространства.Находим критическое значение Gкриз таблицы распределения Кохрена по числу степеней свободы числителя f=K-1, знаменателя f=N и уровню значимости q (Приложение Б2). При условии, что Gкр = 0,9; Gр = 0,31; Gкр > Gр, соответственно гипотеза об однородности дисперсий принимается. 5. Расчет оценок коэффициентов уравнения регрессии: Расчет оценок коэффициентов уравнения регрессии производится по методу наименьших квадратов, при этом минимизируется сумма квадратов отклонений между экспериментальными значениями исследуемого параметра и значениями, вычисленными для тех же точек факторного пространства по уравнению регрессии. Вычислим коэффициенты регрессии, характеризующие линейные эффекты:
b1 = 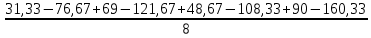 = -28,5; = -28,5;b2 = 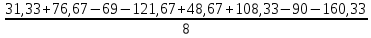 = -22; = -22;b3 = 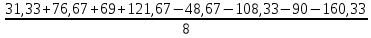 = -13,58. = -13,58.Вычислим коэффициенты регрессии, характеризующие эффекты взаимодействия:
b12 = 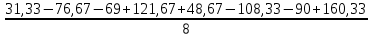 = 2,25; = 2,25;b13 = 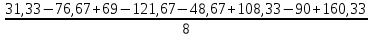 = 4; = 4;b23 = 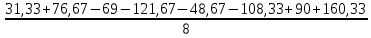 = 1,33; = 1,33;b123 = 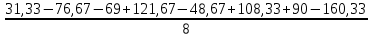 = -0,42. = -0,42.Вычислим свободный член:
b0 =  = 88,25. = 88,25.6. Проверим значимость коэффициентов модели. Гипотезу о статистической значимости (отличии от нуля) коэффициентов регрессии проверяют по критерию Стьюдента. Расчетное значение tpэтого критерия определяют как частное от деления модуля коэффициента biна оценку его среднеквадратического отклонения 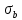 : :
В ПФЭ, благодаря одинаковой удаленности всех экспериментальных точек факторного пространства от центра эксперимента, оценки всех коэффициентов уравнения регрессии независимо от их величины вычисляются с одинаковой погрешностью (при выполнении условия воспроизводимости опытов):
где 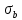 - оценка дисперсии воспроизводимости эксперимента - оценка дисперсии воспроизводимости эксперимента
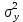 = = 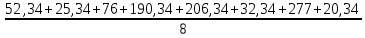 = 110; = 110;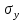 = = 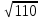 = 10,49; = 10,49;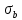 = = 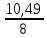 = 1,31, отсюда значения = 1,31, отсюда значения  : : = = 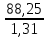 = 67,37; = 67,37; = = 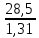 = 21,76; = 21,76;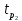 = = 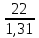 = 16,79; = 16,79;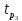 = =  = 10,37; = 10,37;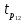 = = 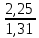 = 1,79; = 1,79;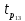 = =  = 3,05; = 3,05;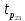 = =  = 1,02; = 1,02;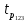 = = 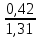 = 0,32. = 0,32.Критическое значение критерия tкрнаходим из таблицы распределения Стьюдента по числу степеней свободы f=N(K–1) и уровню значимости q (Приложение Б3).  = 2,120 = 2,120Если  > > , гипотеза о значимости коэффициента bi принимается , гипотеза о значимости коэффициента bi принимаетсяМы видим что  , , , ,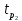 , ,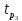 , ,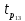 больше больше , поэтому делаем заключение что коэффициенты b0,b1, b2,b3,b13 являются значимыми, тогда как , поэтому делаем заключение что коэффициенты b0,b1, b2,b3,b13 являются значимыми, тогда как 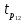 , ,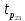 , , 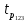 меньше меньше  , а следовательно коэффициенты b12,b23, b123 являются незначимыми и приравниваются к нулю. , а следовательно коэффициенты b12,b23, b123 являются незначимыми и приравниваются к нулю.7. Проверим адекватность полученной модели. Для проверки гипотезы об адекватности ММ необходимо сравнить две дисперсии: а) дисперсию неадекватности, зависящую от разности между значениями yip, рассчитанными по ММ, и экспериментальными результатами yit:
где L – число значимых коэффициентов исследуемого уравнения регрессии, не считая b0; б) дисперсию неоднородности, характеризующую погрешности наблюдений:
Заметим, что дисперсия погрешности наблюдений может быть оценена лишь путем сравнения результатов нескольких параллельных опытов, проводимых в каждой экспериментальной точке. Составим вспомогательную таблицу. Таблица 3.
Находим значения  для каждого опыта: для каждого опыта: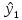 = 88,25-28,5-22-13,58+2,25+4+1,33+0,42 = 32,17; = 88,25-28,5-22-13,58+2,25+4+1,33+0,42 = 32,17;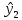 = 88,25+28,5-22-13,58-2,25-4+1,33-0,42 = 75,83; = 88,25+28,5-22-13,58-2,25-4+1,33-0,42 = 75,83;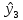 = 88,25-28,5+22-13,58-2,25+4-1,33-0,42 = 68,17; = 88,25-28,5+22-13,58-2,25+4-1,33-0,42 = 68,17; = 88,25+28,5+22-13,58+2,25-4-1,33+0,42 = 122,51; = 88,25+28,5+22-13,58+2,25-4-1,33+0,42 = 122,51;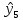 = 88,25-28,5-22+13,58+2,25-4-1,33-0,42 = 47,83; = 88,25-28,5-22+13,58+2,25-4-1,33-0,42 = 47,83; = 88,25+28,5-22+13,58-2,25+4+1,33-0,42 = 110,99 = 88,25+28,5-22+13,58-2,25+4+1,33-0,42 = 110,99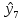 = 88,25-28,5+22+13,58-2,25-4-1,33+0,42 = 88,17; = 88,25-28,5+22+13,58-2,25-4-1,33+0,42 = 88,17;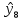 = 88,25+28,5+22+13,58+2,25+4+1,33+0,42 = 160,33. = 88,25+28,5+22+13,58+2,25+4+1,33+0,42 = 160,33.Вычислим дисперсию неадекватности: 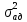 = = 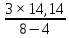 = 10,61 = 10,61Адекватность ММ проверяется по F – критерию Фишера. Его расчетное значение находят как частное от деления оценки дисперсии неадекватности на оценку дисперсии единичного наблюдения. Если это условие не выполняется, их нужно поменять местами. Критическое значение Fкрнаходят из таблицы распределения Фишера по числу степеней свободы числителя f = K(N–L) = 12, знаменателя f=N(K–1)=16, К – число повторностей опыта,и уровню значимости q (Приложение Б4). Если Fр>Fкргипотеза об адекватности отклоняется. Fр =  = = 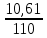 = 0,1; = 0,1;Fкр = 2,42. Отсюда следует, что Fр 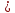 Fкр, а следовательно можно сделать вывод что математическая модель адекватна. Fкр, а следовательно можно сделать вывод что математическая модель адекватна.Список использованной литературы 1. Сборник заданий и методическое руководство к курсовой работе по курсу аналитические и численные методы в планировании экспериментов и инженерном анализе: Учебно-методическое пособие. /Сост. С.С. Алатырев.-Чебоксары: ФГБОУ ВО ЧГСХА, 2016. - 20с. 2. Спирин Н.А., Лавров В.В. Методы планирования и обработки результатов инженерного эксперимента Екатеринбург: ГОУ ВПО УГТУ-УПИ. – 257с., 2004 [электронный ресурс] window.edu.ru/resource/524/28524/ files/ustu131.pdf. 3. Рыжков И.Б. Основы научных исследований и изобретательства: учеб. пособие, СПб. ;М. ; Краснодар: Лань, 2013. 4. Спиридонов А.А. Планирование эксперимента при исследовании технологических процессов М.: Машиностроение, 1981. 5. Мишин П.В., Хузин В.Х. Основы научных исследований, Чебоксары: Полиграфический отдел ФГОУ ВПО «Чувашская ГСХА», 2004. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 jt
jt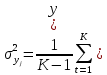 jt - ȳj)2;
jt - ȳj)2;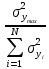 ;
;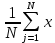 ij ȳj;
ij ȳj;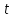 р =
р = 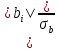
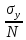 ,
, yj
yj  ,
,