курсовая по автоматизации. Курсовая работа по дисциплине Автоматизация в электромеханике
 Скачать 344.23 Kb. Скачать 344.23 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет» Кафедра электротехники и электромеханики Курсовая работапо дисциплине: «Автоматизация в электромеханике» «Расчет системы автоматического управления двигателем постоянного тока независимого возбуждения»Выполнил студент гр. ЭМ- 20-1б Шалабот С.С. Проверил преподаватель Кавалеров Б.В. Оценка дата Пермь 2023 Цель курсовой работы Применить полученные на лекционных, практических и лабораторных занятиях, а также при выполнении самостоятельной подготовки и изучении дополнительной литературы знания, умения и навыки для расчета системы автоматического управления двигателем постоянного тока независимого возбуждения. Задачи курсовой работы Получить математическую модель двигателя постоянного тока (ДПТ) на основании его номинальных данных и паспортных параметров. Составить алгоритмическую структурную схему ДПТ. Получить передаточную функцию ДПТ по заданию и по возмущению. Получить математическую модель преобразователя. Рассчитать регулятор системы автоматического управления (САУ) ДПТ. Проанализировать показатели качества синтезированной САУ ДПТ. Выполнить программную реализацию и получить переходные процессы в системе визуального моделирования Matlab/Simulink(лицензия № 568405). Проанализировать полученные результаты и сделать выводы. Объект исследования Система автоматического управления частотой вращения двигателя постоянного тока независимого возбуждения. Предмет исследования Математическая модель САУ частотой вращения ДПТ. Номинальные данные и параметры двигателя 2ПН100МУХЛ4 Мощность – 3,6 кВт Напряжение – 110 В Номинальная частота вращения – 3150 об/мин Максимальная частота вращения – 4000 об/мин Коэффициент полезного действия – 78,5% Сопротивление обмотки якоря при 15ᴼС – 0,084 Ом Сопротивление обмотки добавочных полюсов при 15ᴼС – 0,089 Ом Сопротивление обмотки возбуждения при 15ᴼС – 129 Ом Индуктивность цепи якоря – 1 мГн Момент инерции – 0,015 кг*м^2 Содержание курсовой работы Получение математической модели двигателя постоянного тока (ДПТ) на основании его номинальных данных и паспортных параметров. Полное сопротивление якорной цепи: 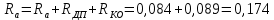 (Ом) (1) (Ом) (1)где Ra– сопротивление обмотки якоря, RДП – сопротивление добавочных полюсов, RКО – сопротивление компенсационной обмотки. Нагретое сопротивление якорной цепи: 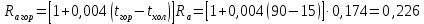 (Ом) (2) (Ом) (2)где tхол = 15ºС, tгор = 90ºС. Электромагнитная постоянная времени: 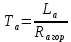 = =  (с) (3) (с) (3) 1.4. Номинальный ток якоря двигателя: 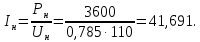 (А) (4) (А) (4)1.5. Угловая скорость якоря двигателя номинальная: 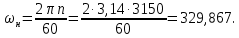 (рад/с) (5) (рад/с) (5)1.6. Коэффициент ЭДС двигателя: 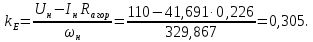 (В·с) (6) (В·с) (6)1.7. Угловая скорость якоря холостого хода: 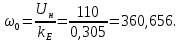 (рад/с) (7) (рад/с) (7) 1.8. Номинальный вращающий момент двигателя: 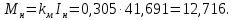 (Н·м) (8) (Н·м) (8)1.9. Ток короткого замыкания двигателя: 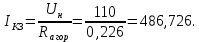 (А) (9) (А) (9)1.10. Электромеханическая постоянная двигателя:  (с) (10) (с) (10)1.11. Номинальная ЭДС двигателя: 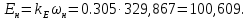 (В) (11) (В) (11)1.12. Момент короткого замыкания двигателя: 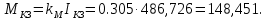 (Нм) (12) (Нм) (12)1.13. Механическая характеристика двигателя: 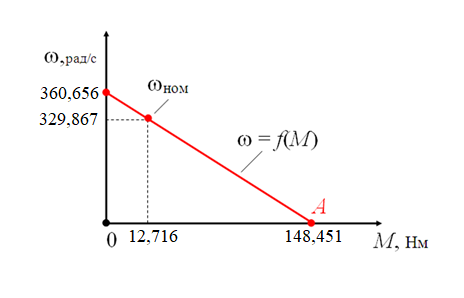 Рисунок 1 – Механическая характеристика двигателя Составить алгоритмическую структурную схему ДПТ Алгоритмическая структурная схема ДПТ 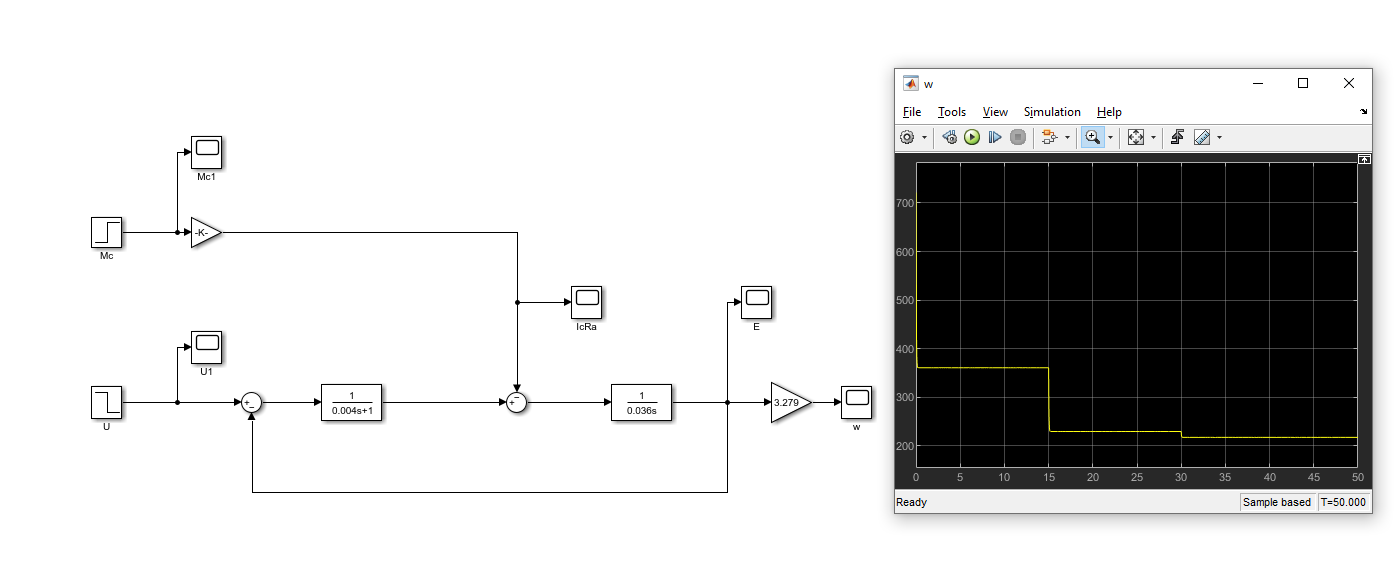 Рисунок 2 – Структурная схема ДПТ Для того, чтобы иметь возможность явно измерять ток якоря, преобразуем эту структурную схему к преобразованному виду (рисунок 3). 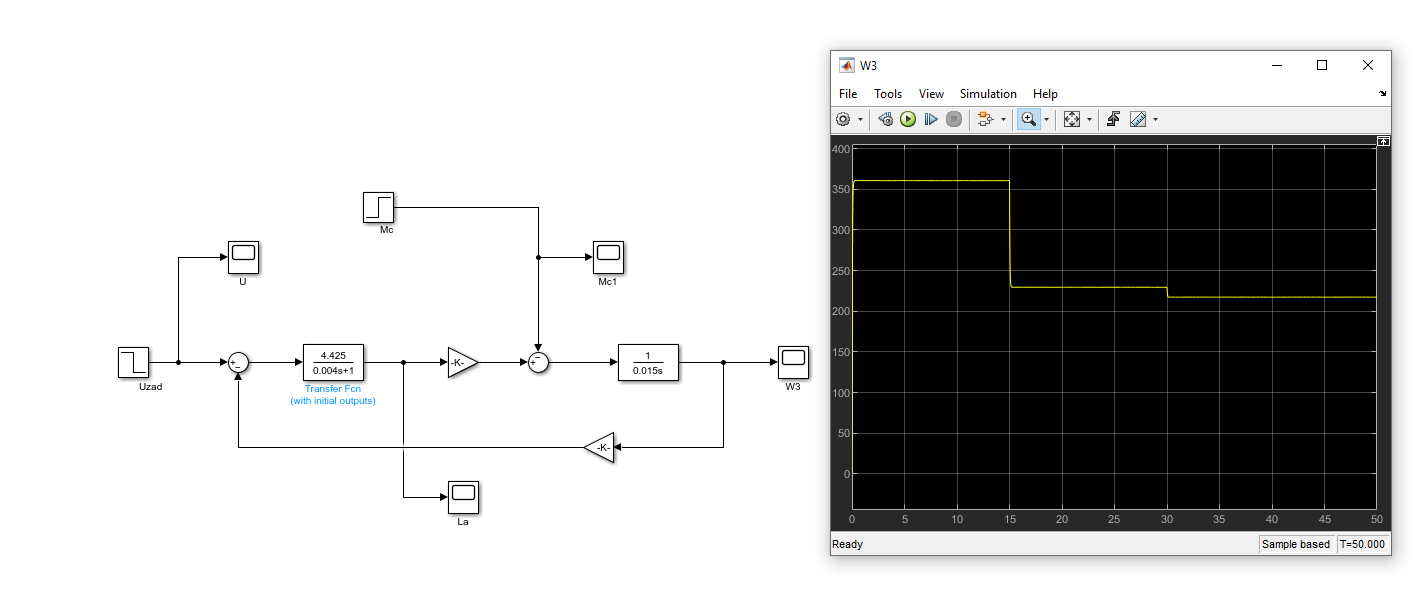 Рисунок 3 – Структурная схема ДПТ Получение передаточной функции ДПТ по заданию и по возмущению. Сначала получить в общем виде, потом подставить конкретные численные значения. Передаточная функция ДПТ по заданию: 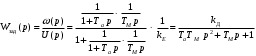 . (13) . (13)Подставив значения параметров: 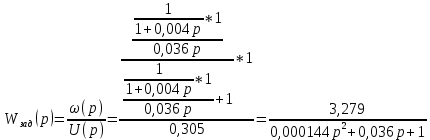 Передаточная функция ДПТ по возмущению: Подставив значения параметров: 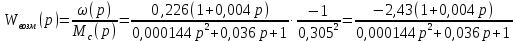 Получение математической модели преобразователя. Учитывая сильное влияние на тиристорный преобразователь (ТП) импульсных помех, на входе СИФУ устанавливают фильтр в виде апериодического звена с постоянной времени TФ = 0,003 – 0,005 с. В этом случае влияние дискретности и полууправляемости можно не учитывать. Выпрямленная ЭДС тиристорного выпрямителя:  , (15) , (15)где g = 1 – нулевая схема, g = 2 – мостовая схема, E2 – действующее значение ЭДС вторичной обмотки. Ed0 = 1,17 E2 – для нулевой схемы, Ed0 = 2,34 E2 – для мостовой схемы. При моделировании параметры тиристорного преобразователя относят к эквивалентным параметрам системы ТП – ДПТ в виде суммы сопротивления якорной цепи двигателя и сопротивления ТП (рисунок 4):  , (16) , (16)аналогично для индуктивностей: 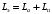 , (17) , (17)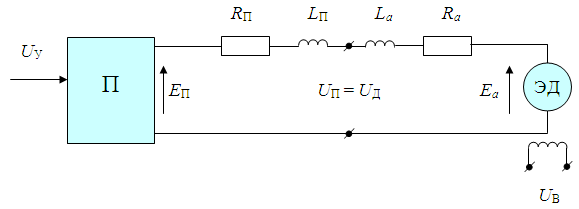 Рисунок 4 – Модель ДПТ и ТП Рассчитать эквивалентные параметры системы ТП – ДПТ по формуле (18). 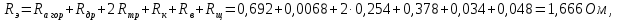 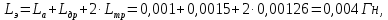 (18) (18)где Rв – сопротивление открытых вентилей (принять: 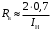 ), Rщ – сопротивление пары щеток (для угольно-графитовых принять падение напряжения на пару щеток ΔUщ =2,0 В, тогда ), Rщ – сопротивление пары щеток (для угольно-графитовых принять падение напряжения на пару щеток ΔUщ =2,0 В, тогда 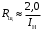 ), Rд, Lд – сопротивление и индуктивность дросселя, устанавливаемого для уменьшения пульсаций якорного тока при питании от тиристорных преобразователей, Rтр, Lтр – сопротивление и индуктивность трансформатора. ), Rд, Lд – сопротивление и индуктивность дросселя, устанавливаемого для уменьшения пульсаций якорного тока при питании от тиристорных преобразователей, Rтр, Lтр – сопротивление и индуктивность трансформатора.Принять Rтр = 0,254 Ом, Lтр = 0,00126 Гн ; Rд = 0,0068 Ом, Lд = 0,0015 Гн. Пересчитать по формулам (19 – 28) эквивалентные параметры электромеханической системы с учетом ТП. Электромагнитная постоянная времени: 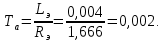 (с) (19) (с) (19)Номинальный ток якоря двигателя: 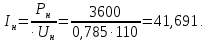 (А) (20) (А) (20)Угловая скорость якоря двигателя номинальная:  (рад/c) (21) (рад/c) (21)Коэффициент ЭДС двигателя: 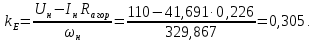 (В с) (22) (В с) (22)Угловая скорость якоря холостого хода: 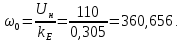 (рад/c) (23) (рад/c) (23)Номинальный вращающий момент двигателя: 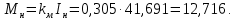 (Н м) (24) (Н м) (24)Ток короткого замыкания двигателя: 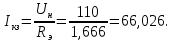 (А) (25) (А) (25)Электромеханическая постоянная двигателя: 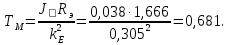 (с) (26) (с) (26)Номинальная ЭДС двигателя: 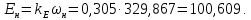 (В) (27) (В) (27)Момент короткого замыкания двигателя: 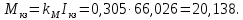 (Н м) (28) (Н м) (28)Учесть момент инерции исполнительного механизма Jмех = 10 кг м2, при номинальной частоте вращения исполнительного механизма nмех = 150 об/мин. 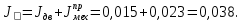 (19) (19)где 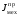 – приведенный момент инерции исполнительного механизма – приведенный момент инерции исполнительного механизма ( 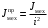 =10/212 , i =21 – передаточное число редуктора). =10/212 , i =21 – передаточное число редуктора).Рассчитать электромеханическую постоянную времени (10) с учетом 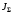 . .Постоянную времени ТП с учетом фильтрации принять равной: Tп = 0,005 с. Поэтому ТП учесть приближенно апериодическим звеном с постоянной времени Tп и коэффициентом усиления k = 48: 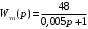 (20) (20)Аналогично (3.1) найти передаточные функции ДПТ с эквивалентными параметрами (с учетом параметров ТП) по заданию и по возмущению. 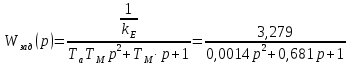 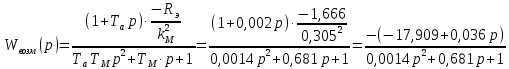 Расчет регулятора одноконтурной системы автоматического управления (САУ) ДПТ. Одноконтурные САР скорости (без применения контура тока) нашли некоторое применение в маломощных приводах постоянного тока. Для ограничения величины тока используют упреждающее токоограничение или отсечку по току. В настоящее время применяются редко, хотя в микропроцессорных системах для повышения быстродействия возможно переключение с двухконтурных САР на одноконтурные. Получить структурную схему САУ ДПТ (рисунок 5). 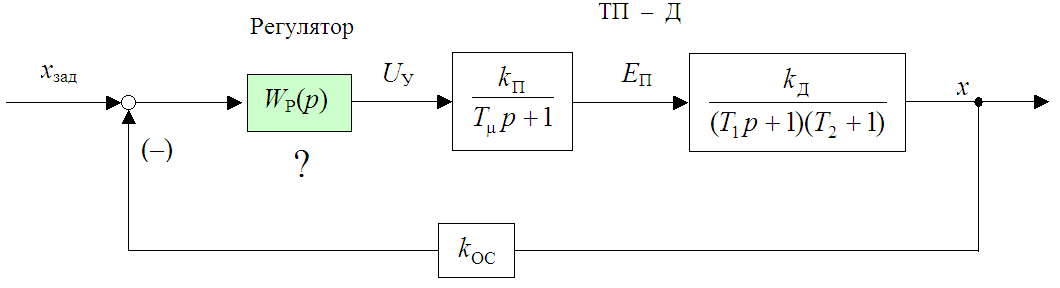 Рисунок 5 – САУ ДПТ При этом для упрощения принять, что kОС = 1. Тиристрный преобразователь считать реверсивным. Выполнить синтез регулятора для ДПТ с передаточной функцией следующего вида: 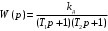 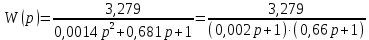 Найти регулятор: а) если T1 >> T2 и T2 ≈ TТП – одного порядка, тогда выбирают Tμ =T2 + TТП= = 0,005 + 0,002= 0,007 и выбирают ПИ-регулятор; Параметры регуляторов определяют из соотношения: 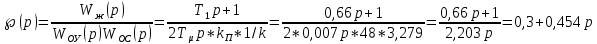 (21) Где 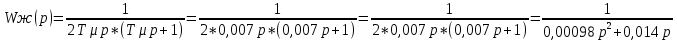 – желаемая передаточная функция разомкнутого контура (модульный оптимум). Зарисовать структурную схему САУ ДПТ с рассчитанным регулятором. 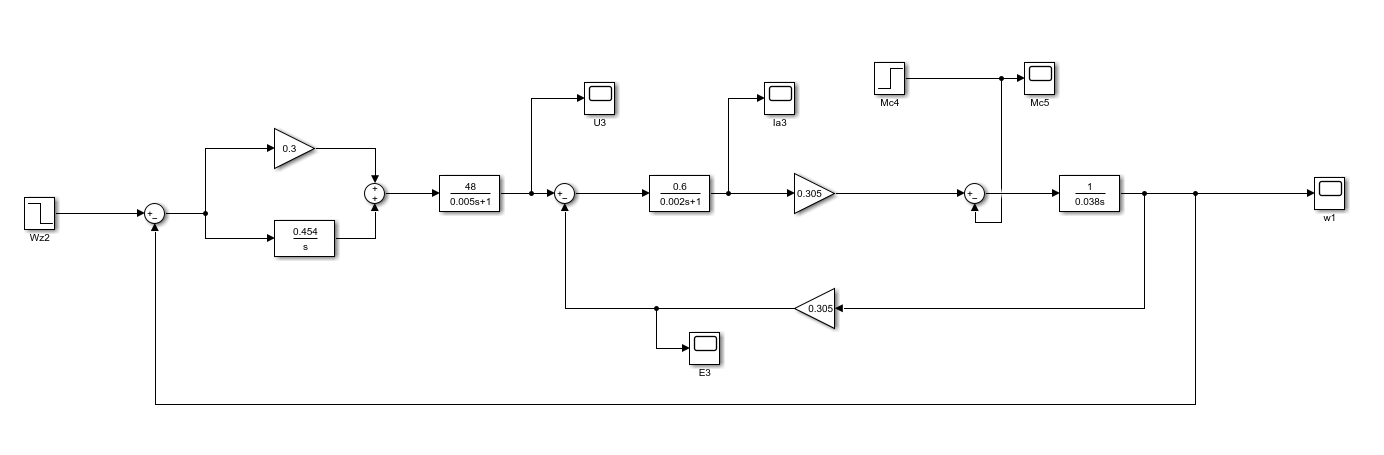 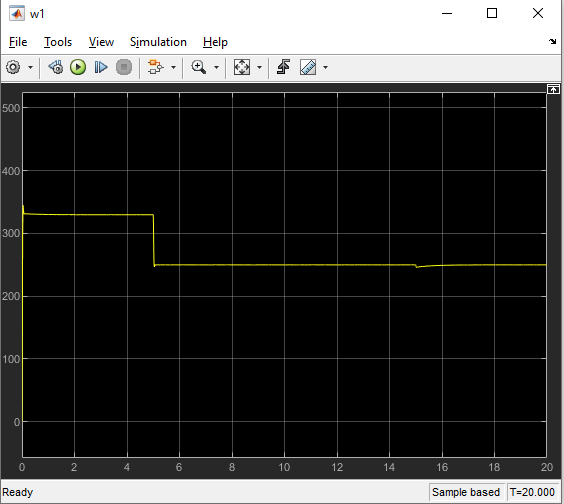 Рисунок 6 – САУ ДПТ с ПИ-регулятором, настроенным на МО Проанализировать показатели качества синтезированной САУ ДПТ (с ПИ и ПИД-регуляторами). Выполнить программную реализацию и получить переходные процессы в системе визуального моделирования Matlab/Simulink (лицензия № 568405). Для ПИД-регулятора малая некомпенсированная постоянная времени равна: Tμ = TТП = 0,005 с. Параметры регуляторов определяют из соотношения: 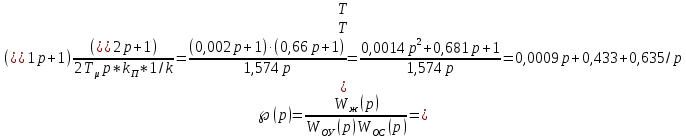  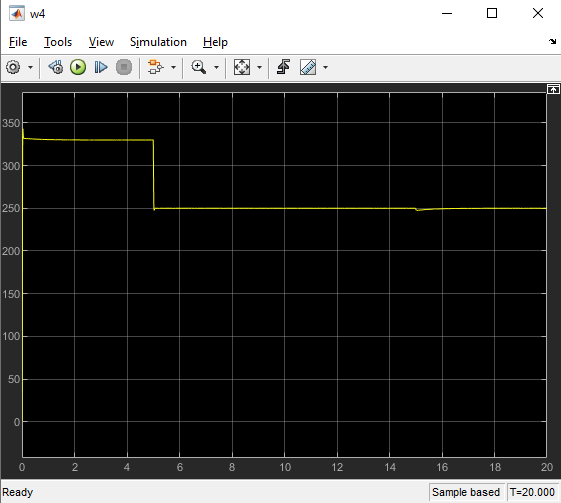 Рисунок 7 - САУ ДПТ с ПИД-регулятором 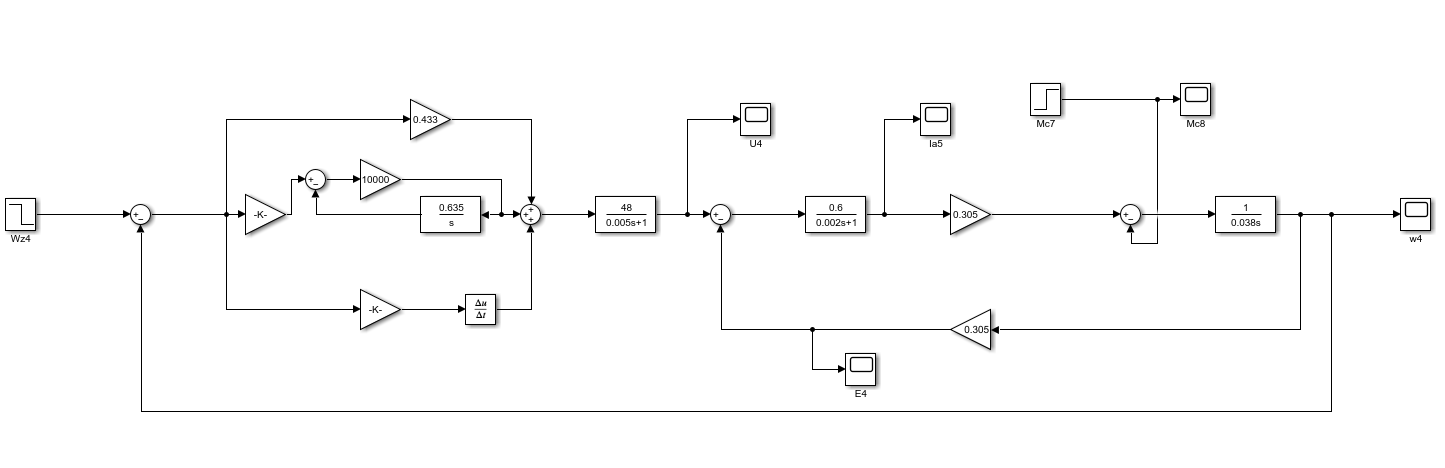 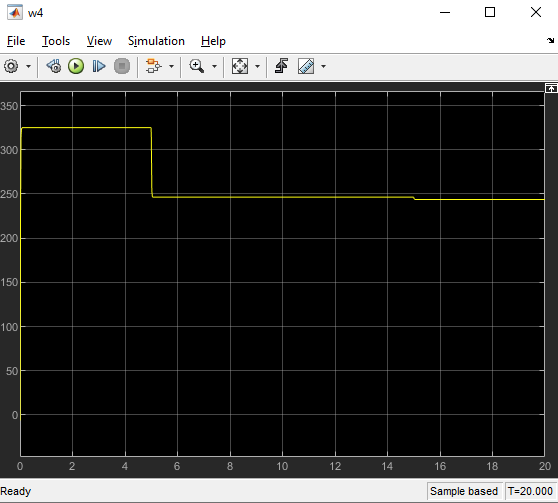 Рисунок 8 – САУ ДПТ с модифицированным ПИД-регулятором Получить и нарисовать графики угловой скорости ДПТ, тока якоря, электромагнитного момента ДПТ при изменении сигнала задания (снижение угловой скорости ДПТ на 15-30 %) и при изменении сигнала возмущения (наброс нагрузки на ДПТ). Учесть, что тиристорный преобразователь принят реверсивным. 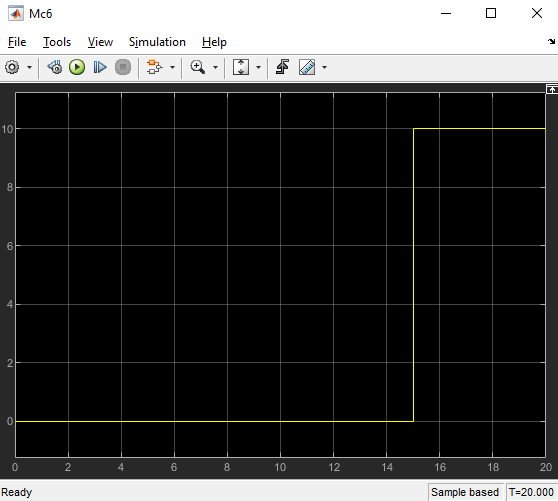 Рисунок 9 – график электромагнитного момента ДПТ с ПИ-регулятором 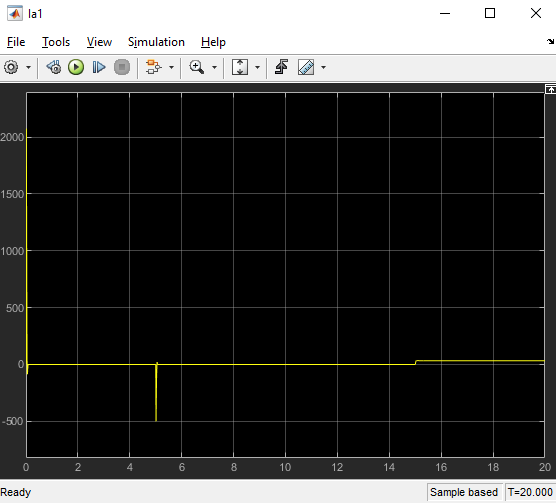 Рисунок 10 – график тока якоря ДПТ с ПИ-регулятором Максимальный ток при переходном процессе превышает номинальный в 12 раз, поэтому при реализации необходимо ограничивать максимальный ток якоря (использовать токоограничительное реле). Imax1=500,5 A, Iном= 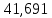 A AПревышение: Imax/Iном=500,5/ 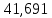 =12 =12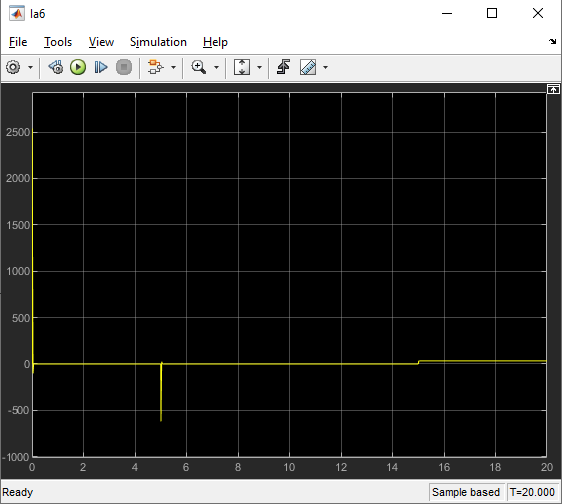 Imax2=619,5 A - максимальный ток при переходном процессе. Максимальный ток при переходном процессе у ПИД-регулятора превышает в 1,24 раза максимальный ток при переходном процессе у ПИ-регулятора. Превышение: Imax2/Imax1=619,5/500,5 =1,24 Imax1 - максимальный ток при переходном процессе у ПИ-регулятора Imax2 - максимальный ток при переходном процессе у ПИД-регулятора Сравнить полученные в п.6 показатели качества переходного процесса САУ (перерегулирование и время нарастания) с показателями настройки на модульный оптимум (σ = 4,3 %, tН = 4,7 Tµ). σ = 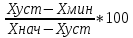 1) У рассчитанного ПИ-регулятора: (Теор: tН = 4,7Tμ =0,0329 с.) Перерегулирование: σ = 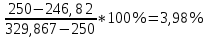 , что меньше теоретического значения. , что меньше теоретического значения.Время нарастания: 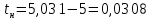 c c0,032/Tµ=0,0308/0,007=4,4 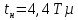 , что меньше теоретического значения. , что меньше теоретического значения.2)У рассчитанного ПИД-регулятора: (Теор: tН = 4,7Tμ =0,0235 с.) Перерегулирование: σ = 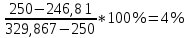 , что меньше теоретического значения. , что меньше теоретического значения.Время нарастания: 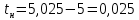 c c0,025/Tµ=0,025/0,005=5 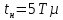 , что больше, чем теоретическое значение. , что больше, чем теоретическое значение.3)У модифицированного ПИД-регулятора: (Теор: tН = 4,7Tμ =0,0235 с.) Перерегулирование: σ = 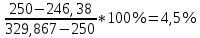 , что больше теоретического значения, но максимально приближено к нему. , что больше теоретического значения, но максимально приближено к нему.Время нарастания: 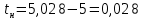 c c0,028/Tµ=0,028/0,005=5,6 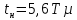 . .6.4. Оценить возможное отличие полученных результатов моделирования и желаемого переходного процесса. Сделать выводы. Наилучшее быстродействие у модифицированного ПИД-регулятора 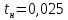 c (Теор: tН = 4,7Tμ =0,0235 с.) c (Теор: tН = 4,7Tμ =0,0235 с.)Среднее быстродействие у рассчитанного ПИД-регулятора 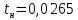 c (Теор: tН = 4,7Tμ =0,0235 с.) c (Теор: tН = 4,7Tμ =0,0235 с.)Худшее быстродействие у ПИ-регулятора  c c (Теор: tН = 4,7Tμ =0,04606 с.) c c (Теор: tН = 4,7Tμ =0,04606 с.)У рассчитанного ПИД-регулятора время нарастания незначительно, но хуже теоретического, а именно в 1,06 раза. Теоретическое время нарастания tн=0,0235 с; значение, полученное в результате расчета tн1=0,025 с. Превышение: 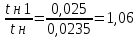 У модифицированного ПИД-регулятора перерегулирование практически совпадает с теоретическим значением: 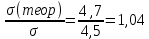 Вывод: Я считаю, что улучшенный ПИД-регулятор является самым лучшим из рассчитанных регуляторов, т.к. он имеет самое лучшее перерегулирование, которое максимально приближено к модульному оптимуму, но в отличие от обычного ПИД-регулятора имеет большее время нарастания, хоть и максимально приближенное к нему. |
