Курсовая работа По дисциплине Дополнительные главы сопротивления материалов
 Скачать 299.46 Kb. Скачать 299.46 Kb.
|
                                                               Министерство образования и науки Российской Федерации Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Новосибирский государственный технический университет» Кафедра "Прочность летательных аппаратов" Курсовая работа По дисциплине Дополнительные главы сопротивления материалов Студент: Денисов Дмитрий Сергеевич Группа: ПС-52 Преподаватель: Белоусова Елена Николаевна Новосибирск 2017 1.Решение нелинейных уравнений Постановка задачи Двутавровая балка закреплена на двух шарнирных опорах и нагружена в соответствии с расчетной схемой, как показано на рисунке 1.1. Исходные данные и механические характеристики представлены в Таблице №1. Требуется:
Таблица №1 Исходные данные
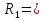 69,333 69,333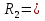 52,667 52,667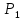 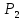 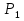 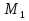 q 1 2 3 4 5 6 7 a a a a a a Рис. 1.1. Расчетная схема Определение перерезывающих сил и изгибающих моментов Выбираем систему координат (начало системы координат совмещено с левым по рис. 1.1 концом балки) и разбиваем балку на силовые участки. Границы силовых участков обозначены цифрами 1-7. Определяем реакции опор: 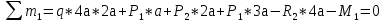 (1.1) 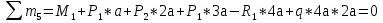 Из (1.1) находим 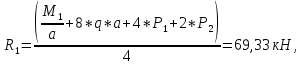 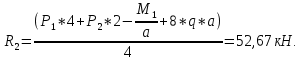 Найденные значения для 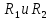 подписываем на расчетной схеме (рис.1.1). подписываем на расчетной схеме (рис.1.1).Последовательно рассматриваем силовые участки и записываем уравнения для Q и M. Участок 1-2 (0≤х≤а) Характерные значения: 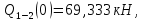 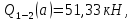 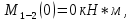 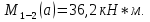 Участок 2-3 (а≤х≤2а) Характерные значения: 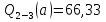 кН, кН,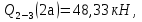 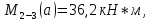 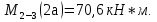 Участок 3-4 (2а≤x≤3а) Характерные значения: 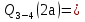 28,33 кН, 28,33 кН,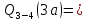 10,33 кН, 10,33 кН,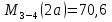 кН*м, кН*м,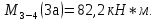 Участок 4-5 (3а≤х≤4а) Характерные значения: 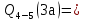 -4,66 кН, -4,66 кН,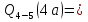 -22,66 кН, -22,66 кН,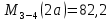 кН*м, кН*м,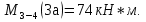 Участок 5-6 (4а≤х≤5а) Характерные значения: 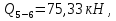 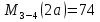 кН*м, кН*м,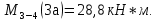 Участок 6-7 (5а≤х≤6а) Характерные значения: 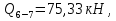 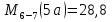 кН*м, кН*м,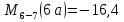 кН*м. кН*м.Расчет балки на полную статическую прочность при изгибе Номер двутаврового сечения балки определяем из расчета на прочность по максимальным нормальным напряжениям. В сечении с 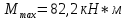 должно выполняться условие 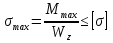 , откуда находим потребный момент сопротивления балки , откуда находим потребный момент сопротивления балки 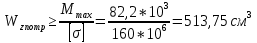 По ГОСТу 8239-72 выбираем ближайший по моменту сопротивления двутавровый профиль №30а с 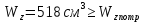 . В этом случае наибольшее нормальное напряжение . В этом случае наибольшее нормальное напряжение 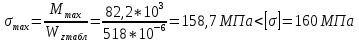 . .Схематическое изображение сечения представлено на рис. 1.2. Геометрические жесткостные параметры двутаврового профиля представлены в таблице 1.2. 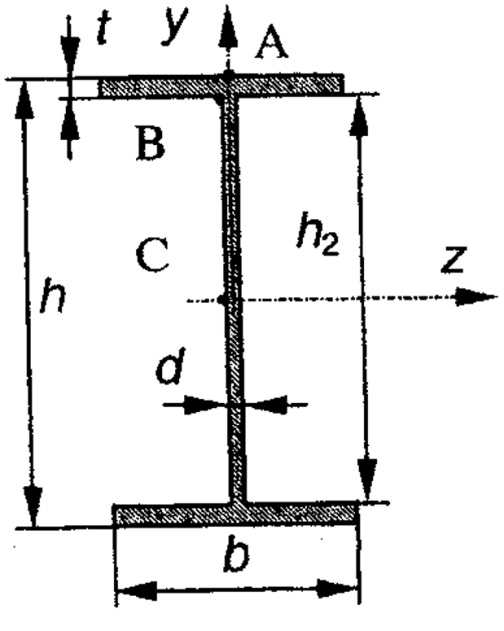 Рис. 1.2. Сечение двутаврового профиля Параметры профиля Таблица 1.2
Выполняем проверку прочности двутавра №30а по максимальным касательным напряжениям. В сечении с максимальным значением перерезывающей силы проверяем на прочность в точке С поперечного сечения балки 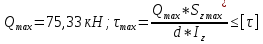 , ,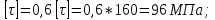 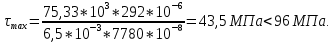 Прочность по максимальным касательным напряжения обеспечена. Проверяем прочность (по четвертой теории прочности) для опасной точки В поперечного сечения балки (рис.1.2), которая соответствует максимальному значению эквивалентного напряжения 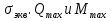 действуют в разных сечениях по длине балки, поэтому сделаем фиктивное сечение, где М и Q имеют максимальные значения. действуют в разных сечениях по длине балки, поэтому сделаем фиктивное сечение, где М и Q имеют максимальные значения.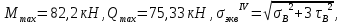 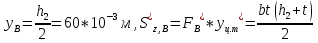 ; ;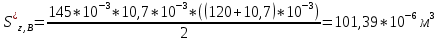 , ,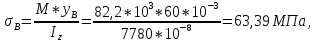 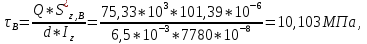 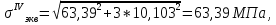 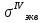 не превышает не превышает 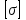 , поэтому выбранный двутавр №30а может быть оставлен в конструкции балки. , поэтому выбранный двутавр №30а может быть оставлен в конструкции балки.Определение прогибов и углов поворотов балки. Для определения прогибов и углов поворота воспользуемся универсальным уравнением упругой линии, которое для балки с постоянной жесткостью имеет вид: 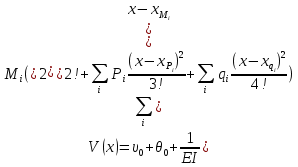 ; ;(1.2) 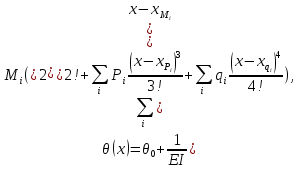 Где 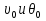 - произвольные постоянные. - произвольные постоянные.В (1.2) под знаками сумм следует учитывать силовые факторы, лежащие слева от рассматриваемого сечения, так что выражения в круглых скобках всегда больше или равны нулю. Распределённая нагрузка 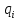 должна заканчиваться на правом конце балки. должна заканчиваться на правом конце балки.В нашем случае будем иметь 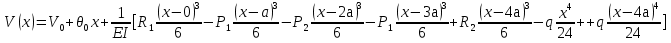 , ,(1.3) 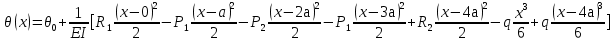 . .Подчеркнутые в (1.3) слагаемые следует учитывать для рассматриваемого сечения лишь тогда, когда выражения в круглых скобках неотрицательно. Произвольные постоянные 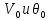 определяется из граничных условий: определяется из граничных условий: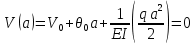 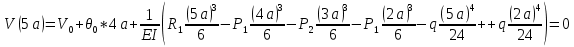 , ,Вычисления по формулам (1.3) удобно проводить с помощью ЭВМ. Пример простой программы для расчета многопролетной балки, составленной на языке Fortran и MathCAD, приведен в приложении 1. Результаты расчетов представлены в виде эпюр Q, M, θ, υ на рис. 1.3.    q a a a a a a 7 6 5 4 3 2 1 Приложение 1 ПРОГРАММЫ ДЛЯ РАСЧЕТА МНОГОПРОЛЕТНОЙ БАЛКИ Ниже приводиться текст программы на языке Fortran. ! Задаем переменные function z(i,j); z=0; if(i>j) z=1; end real,dimension(30)::x,w,w1,w11,w111,v,t real::m1 !Задаем исходные данные P1=14.94; P2=19.8; m1=19.98; q=30; a=0.6; EJ=5.859*10**3 ! Находим реакции опор R2=(P1*4+2*P2-m1/a+3*q*a/2)/4 R1=(m1/a+10.5*q*a+4*P1+2*P2)/4 h=a/4 x(1)=0 !Записываем цикл для нахождения эпюр do i=1,29; x(i+1)=x(i)+h if(i/5*5==i) x(i+1)=x(i); end do do i=1,30; y=x(i) !Записываем уравнение упругой балки перемещения w(i)=+R1*(y-a)**3/6*z(i,5)& -P1*(y-2*a)**3/6*z(i,10)& -P2*(y-3*a)**3/6*z(i,15)& -P1*(y-4*a)**3/6*z(i,20)& +R2*(y-5*a)**3/6*z(i,25)& -q*y**4/24& +q*(y-3*a)**4/24*z(i,15) !Записываем уравнение упругой балки углов поворота w1(i)=+R1*(y-a)**2/2*z(i,5)& -P1*(y-2*a)**2/2*z(i,10)& -P2*(y-3*a)**2/2*z(i,15)& -P1*(y-4*a)**2/2*z(i,20)& +R2*(y-5*a)**2/2*z(i,25)& -q*y**3/6& +q*(y-3*a)**3/6*z(i,15) !Записываем уравнение упругой балки моментов w11(i)=+R1*(y-a)*z(i,5)& -P1*(y-2*a)*z(i,10)& -P2*(y-3*a)*z(i,15)& -P1*(y-4*a)*z(i,20)& +R2*(y-5*a)*z(i,25)& -q*y**2/2& +q*(y-3*a)**2/2*z(i,15) !Записываем уравнение упругой балки сил w111(i)=R1*z(i,5)& -P1*z(i,10)& -P2*z(i,15)& -P1*z(i,20)& +R2*z(i,25)& -q*y& +q*(y-3*a)*z(i,15) end do C1=-1/EJ*(5*w(5)-w(25))/4 C2=-1/EJ*(w(25)-w(5))/(4*a) v=C1+C2*x+w/EJ t=C2+w1/EJ do i=1,30; write(1,*) x(i),v(i),t(i),w11(i),w111(i); end do end Результатом расчета программы приведены ниже в программе MathCAD в виде графиков на рис 1.4. 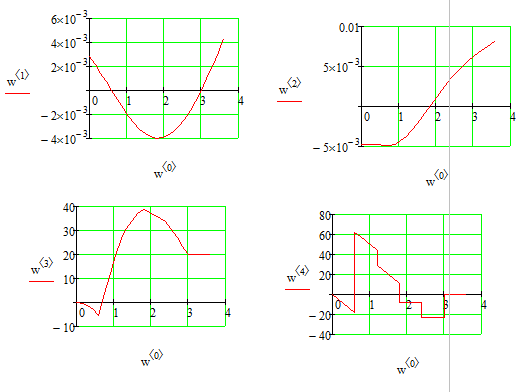 Рис. 1.4. Результаты расчета программы Fortran. Ниже приводится текст программы на языке MathCAD. 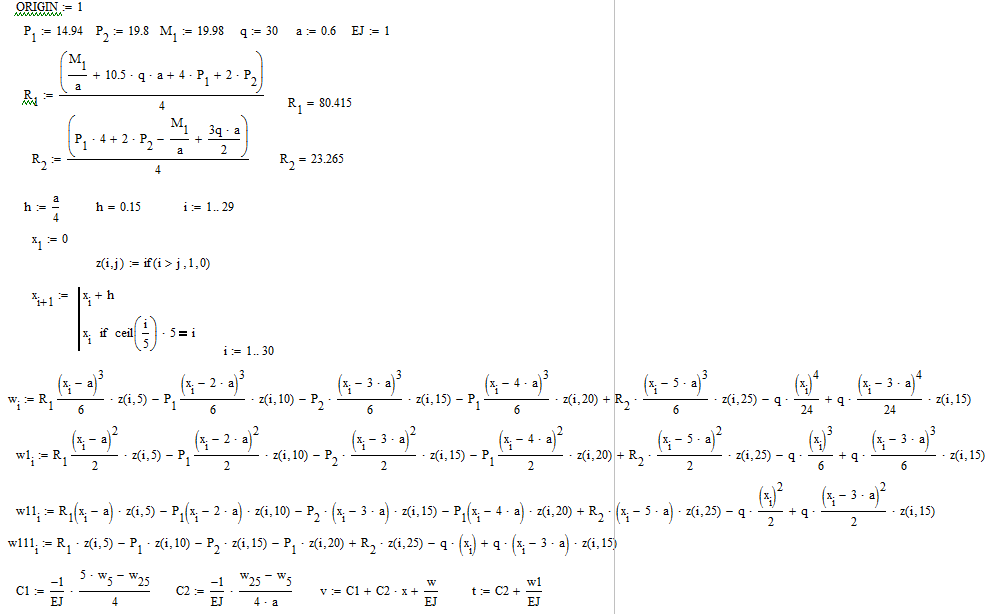 Результаты расчета программы приведены в рис. 1.5. 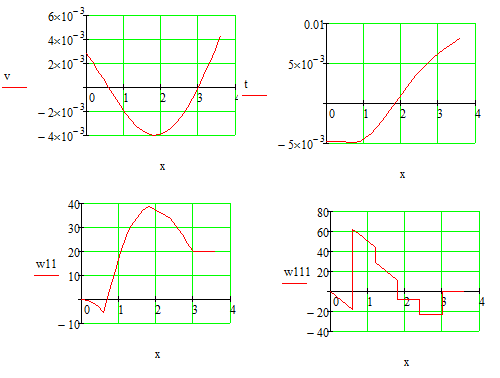 Рис. 1.5. Результаты расчета программы MathCAD. |

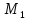 , кН*м
, кН*м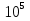
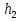 ,мм
,мм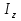 ,
,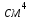
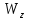 ,
,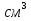
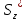 ,
,