пп. Курсовая работа по дисциплине информатика для студентов направления

• Название: Курсовая работа по дисциплине информатика для студентов направления
• Дата: 12.12.2022
• Размер: 378.42 Kb.
• Имя файла: Nikonov.docx
• Тип: Курсовая; #841597

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Тверской государственный технический университет»

«ТвГТУ»

Факультет информационных технологий

Кафедра информатики и прикладной математики

Курсовая работа

по дисциплине ИНФОРМАТИКА

для студентов направления

13.03.01 Теплоэнергетика и теплотехника

Профиль – Автономные энергетические системы

Тема:

ИССЛЕДОВАНИЕ ЧИСЛЕННЫХ МЕТОДОВ ВЫЧИСЛЕНИЯ

ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Вариант 17

Курсовая работа принята:

« » ____________________ 202_ г.

Исполнитель:

студент 1курса

группы Б.ТТ.АЭС.22.04

Никонов А. А.

Защищена

«___»______________________ 202_ г.

С оценкой _______________________

Руководитель: ст. преподаватель

Кошкина Г.В.

Подпись__________________________
Тверь 2022 г.

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Тверской государственный технический университет»

(ТвГТУ)

Факультет информационных технологий

Кафедра информатики и прикладной математики

ЗАДАНИЕ

НА КУРСОВУЮ РАБОТУ по дисциплине ИНФОРМАТИКА

Студент: Никонов Арсений Алексеевич

Направление 13.03.01 «Теплоэнергетика и теплотехника»

Профиль «Автономные энергетические системы»

Тема: ИССЛЕДОВАНИЕ ЧИСЛЕННЫХ МЕТОДОВ ВЫЧИСЛЕНИЯ

ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Задание

1. Вычислить определенный интеграл с заданной точностью ε методами:

1) правых прямоугольников,

2) центральных прямоугольников,

3) левых прямоугольников,

4) трапеций,

5) Симпсона.

Сравнить полученные результаты, сделать выводы.

2. Вычислить значение интеграла аналитически.

3. Исследовать зависимость точности вычисления интеграла ε от числа шагов n.

Сравнить полученные результаты, сделать выводы.

4. Оценить погрешность вычисления интеграла по правилу Рунге;

Дата выдачи задания: «____»._____ 20____ г.

Срок предоставления студентом на кафедру «____» ____________ 20 __ г.

Руководитель:

(ФИО, ученая степень, звание, инициалы) Подпись

Задание получено:

(ФИО студента) Подпись

Оглавление

Введение 4

Теоретическая часть 6

Практическая часть 11

Метод левого треугольника 11

Метод правых треугольников 15

Метод средних треугольников 16

Метод трапеций 17

Метод парабол(Симпсона) 18

Аналитический метод 20

Вывод 21

Оценка погрешности вычисления интеграла по правилу Рунге 22

Список используемой литературы 23

Введение

Численное интегрирование — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов для нахождения значения определённого интеграла.

Численное интегрирование применяется, когда:

1. 
   Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.
   
2. 
   Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции.
   

Для вычисления интеграла применяются: метод прямоугольников, метод трапеций, метод парабол (Симпсона), которые будут рассмотрены в данной работе, а также метод Гаусса и его вариации.

Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах.

Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями.

Формула Симпсона (также Ньютона-Симпсона) относится к приёмам численного интегрирования. Суть метода заключается в приближении подынтегральной функции на отрезке{\displaystyle [a,b]} интерполяционным многочленом второй степени{\displaystyle p_{2}(x)}, то есть приближение графика функции на отрезке параболой.

Увеличение точности

Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла.

Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них.

При стремлении количества разбиений к бесконечности оценка интеграла стремится к его истинному значению для аналитических функций для любого численного метода.

Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге, основная идея которого состоит в вычислении приближения выбранным методом с шагом h, а затем с шагом h/2, и дальнейшем рассмотрении разностей погрешностей для этих двух вычислений.

Теоретическая часть

Далее представлено более подробное рассмотрение численных методов.

Метод прямоугольников разделяется на методы левых, правых и средних прямоугольников.

В случае левых прямоугольников приближенное значение интеграла получается в виде суммы площадей n прямоугольников, высота которых равна значению f(x) на левом краю каждого подинтервала (рис.1).

Формула принимает вид:



Если в качестве приближенного значения площади для каждого подинтервала принять площадь прямоугольника, высота которого равна значению f(x) на правом краю подинтервала (рис. 2), то формула численного интегрирования имеет вид:



Третья модификация метода прямоугольников – метод «средних» прямоугольников. В этом случае в качестве приближенного значения площади для каждого подинтервала принимается площадь прямоугольника, высота которого равна значению f(x) в средней точке подинтервала (рис. 3), а формула численного интегрирования имеет вид:



Метод прямоугольников является наиболее простым и вместе с тем наиболее грубым методом приближенного интегрирования. Очевидно, что чем больше будет число n отрезков разбиения, тем более точный результат дадут формулы, приведённые выше. Однако увеличение числа отрезков разбиения промежутка интегрирования не всегда возможно. Поэтому большой интерес представляют формулы, дающие более точные результаты при том же числе точек разбиения.



1) Метод левых прямоугольников



2) Метод правых прямоугольников



3) Метод средних прямоугольников
В методе трапеций отрезок [a; b] так же разбивается на n равных частей. На каждом отрезке кривая y = f(x) заменяется прямой, проходящей через две известные и строится прямоугольная трапеция с высотой h.

Тогда искомая площадь криволинейной трапеции приближенно

заменяется суммой площадей элементарных геометрических трапеций.

Площадь такой фигуры будет более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников, что даёт большую точность вычислений, при том же количестве разбиений. В этом случае формула принимает вид:



Так же этот метод может быть получен путём вычисления среднего арифметического между результатами применения формул правых и левых прямоугольников.


4) Метод трапеций

Идея метода парабол (Симпсона) исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает кривой y = f(x), чем хорда, соединяющая концы дуги этой кривой (метод трапеций). Поэтому значения площадей соответствующих элементарных трапеций, ограниченных сверху дугами парабол, являются более близкими к значениям площадей соответствующих частичных криволинейных трапеций, ограниченных сверху дугой кривой y = f(x), чем значения площадей соответствующих прямолинейных трапеций.

Малая формула Симпсона дает интеграл с хорошей точностью, когда

график подынтегральной функции мало изогнут, в случаях же, когда дана более

сложная функция, малая формула Симпсона непригодна. Тогда, чтобы посчитать

интеграл заданной функции нужно разбить отрезок [a, b] на n частей и к каждому

из отрезков применить формулу. Обязательным требованием, вытекающим из геометрического смысла метода парабол, является то, что n должно быть четным.

Формула Симпсона не проходит проверку на величину погрешности в случае узких (малое число точек на пик) пикоподобных функций, оказываясь значительно менее эффективной, чем правило трапеций. Именно, для достижения той же погрешности, что и в случае правила трапеций, составному правилу Симпсона требуется в 1,8 раз больше точек.

Малая формула Симпсона имеет вид:



Большая формула Симпсона имеет вид:



Где



5) Метод парабол (Симпсона)

Так как основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически, возникает погрешность. Как было указано выше, точность вычислений критически зависит от числа разбиений функции, которое всегда ограничено. С целью компенсации этого вводится вычисление погрешности, в частности правило Рунге.

Пусть Ց – заданная точность вычисления интеграла, тогда шаг h должен удовлетворять условию .

Саму оценку погрешности можно произвести следующим методом:

Пусть - приближенное значение интеграла, вычисленное с шагом h, а - значение этого интеграла, вычисленное с шагом2h. Если , где и вычислены по методу Симпсона, или , где и вычислены по методу прямоугольников или трапеций, то в качестве приближенного значения интеграла берут значение .

Если неравенство для соответствующего метода не выполняется, то найденное значение интеграла не удовлетворяет заданной точности. Тогда проводят новые вычисления с шагом и вновь проверяют выполнение неравенств. Этот прием многократного уменьшения шага применяют до тех пор, пока соответствующее неравенство не станет истинным.

Важно отметить, что для того, чтобы оценить точность найденного значения

интеграла по правилу Рунге, необходимо, чтобы первоначальное значение n было

кратно четырем.

Практическая часть

Метод левого треугольника

За шаг разбиения отвечает формула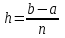



Формула шага разбиения



Далее мы получаем x(h)-то есть от нашего шага разбиения, до тех пор, пока X не будет равен нашему пределу, а точнее, значение = 0,785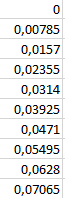



Формула к этому действию, чтобы не писать всё вручную



После получения x(h), нам следует рассчитать по формуле, которая выдавалась по варианту, в моём случае это: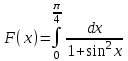



Данные вычисления получаем для всех x(h)

Формула в экселе:



Из полученных нами данных составляем уравнение средней прямой:



Первые десять результаты которые были получены:



Мы используем удвоенный шаг разбиения от первого



Формула:



Далее,рассчитываем x(2h)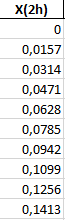



Формула:



После чего, рассчитываем F(x(2h))



Формула:



Из полученных нами данных составляем уравнение средней прямой:



Формула:



Далее, перед тем, как использовать метод левого треугольника мы строим график функции где за Ось(x) у нас отвечает X(2h),а за ось (y) F(x(2h))



При использование метода левых треугольников мы применяем 1 формулы, но сначала для F(x), а затем для F(x(2h))

При методе левых треугольников мы берём сумму от i=0 до n-1 и умноженное на шаг разбиения

Формула по столбцу F(x):



Данные, которые получились:



Для F(x(2h)) проводятся такие же действия

Формула по столбцу F(x(2h)):



Данные, которые получились:



Далее мы производим расчёт погрешности, осуществляется она по вот этой формуле:



Ячейкой I2- у нас является допустимая погрешность:



При проверке погрешности выяснилось, что заданное уравнение выполняется, но значение заданной точности не удовлетворяется



А вот так оно имеет общий вид:

Метод правых треугольников

Взяв данные из прошлого метода, т.к они для всех одни, кроме метода с параболой

Мы рассчитываем данные при помощи метода правого треугольника, берём сумму i=1 до n и умножаем на наш шаг разбиения

Формула по столбцу F(x):



Формула по столбцу F(x(2h)):



И вот какие данные у нас получились:



Далее, для расчёта погрешности, мы берём формулу:



При проверке погрешности выяснилось, что заданное уравнение выполняется, но значение заданной точности не удовлетворяется



Общий вид:

Метод средних треугольников

Взяв данные из прошлого метода, т.к они для всех одни, кроме метода с параболой

Мы рассчитываем данные при помощи метода среднего треугольника, берём сумму по этой формуле(для столбца F(x):



А так же сумму по столбцу F(x(2h)):



И вот какие данные у нас получились:



Далее, для расчёта погрешности, мы берём формулу:



При проверке погрешности выяснилось, что заданное уравнение выполняется и значение заданной точности удовлетворяется



Общий вид:

Метод трапеций

Взяв данные из прошлого метода, т.к они для всех одни, кроме метода с параболой

Мы рассчитываем данные при помощи метода среднего треугольника, берём сумму по этой формуле для столбца F(x):



А так же сумму для столбца F(x(2h)):



И вот какие данные у нас получились:



Далее, для расчёта погрешности, мы берём формулу:



При проверке погрешности выяснилось, что заданное уравнение выполняется и значение заданной точности удовлетворяется



Общий вид:

Метод парабол(Симпсона)

Для данного способа нам понадобятся новые данные, для того чтобы получить шаг разбиения, для начала нужно получить n

По формуле n=(0,785-0)/0,177828

n=4,4

Т.к нам нужно целое число и четное, мы принимаем n за 6

Из этого следует что h=0,785/6

h=0,130833



Формула для h в Excel:



Далее, как и при всех методах, мы рассчитываем X(h):



Формула:



Далее, по нашей формуле считаем F(x):



Формула:



Далее, мы используем удвоенный шаг разбиения от первого

Формула:



Само значение:



Далее, рассчитываем x(2h)



Формула:



После чего, рассчитываем F(x(2h))



Формула:



При использование метода Симпсона мы применяем 1 формулы, но сначала для F(x), а затем для F(x(2h))

Формула по столбцу F(x):



Полученное значение:



Формула по столбцу F(x(2h)):



Полученное значение:



Далее, для расчёта погрешности, мы берём формулу:



При проверке погрешности выяснилось, что заданное уравнение выполняется, но значение заданной точности не удовлетворяется



Общий вид:

Аналитический метод

Вывод

По заданному выражению аналитической функции f (x) = был вычислен приближенно определенный интеграл от этой функции на заданном интервале [a,b]. Было выяснено, что от количества разбиений "n" зависит точность решения. Чем число разбиений больше, тем выше точность измерений.

Оценка погрешности вычисления интеграла по правилу Рунге

Исходя из метода парабол(Симпсона)

Сделаем сравнение

Шаг разбиения полученный в данном способе равен 0,130833, а по методу Рунге шаг разбиения должен быть равен или меньше 1,77828, что соответствует заданному критерию.

Из этого следует, что метод параболы был выполнен верно.

Что не сказать об остальных способах, ведь из-за того, что промежуток довольно таки большой, приходилось брать большое количество разбиений, чтобы добиться более точного результата, ведь как мы уже выяснили, что точно решения зависит от количества разбиения “n”

Список используемой литературы

1. 
   Методический материал предоставленный учителем
   
2. 
   https://studfile.net/preview/6229937/page:3/
   
3. 
   https://studfile.net/preview/962425/page:3/
   
4. 
   https://math.fandom.com/ru/wiki/Определенный_интеграл
   
5. 
   Веденеева Е.А. Функции и формулы Excel 2007. Библиотека пользователя. -СПб.: Питер, 2008. -384 с.