НИЭТ курсач 21 вар. Курсовая работа по дисциплине "надежность изделий электронной техники" (
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
2. Тепловой режим и обеспечение влагозащиты микросхем2.1.Расчет обеспечения тепловой режима гибридной ИСОсновные дестабилизирующие факторы для гибридных интегральных микросхем являются термоактивированными: теплота, выделяющаяся в процессе работы микросхем при неблагоприятных условиях, вызывает перегрев элементов и ускоряет наступление отказов. К таким факторам относятся: 1) превышение максимально допустимых значений электрических параметров полупроводниковых компонентов ИС, в результате чего может возникнуть явление теплового пробоя; 2) Нарушение температурного режима эксплуатации гибридной ИС, т.е. превышение максимально допустимой температуры окружающей среды, в результате чего может нарушиться теплоотвод. Здесь следует также добавить, что максимально допустимая температура окружающей среды определяется в основном конструкцией корпуса (площадь теплового контакта корпуса, материалы различных его частей, линейные размеры и т.д.). Основными понятиями, используемыми при проведении тепловых расчетов, являются: - перегрев элемента (компонента) ИС (, С): разность между температурой элемента и средней температурой поверхности корпуса; - максимально допустимая температура элемента (компонента) ИС (Тmax доп): это температура, при которой обеспечиваются требования по надежности; - удельная мощность рассеяния (Р0, Вт / С): плотность теплового потока от элемента (компонента) ИС, кристалла или платы; - максимально допустимая температура окружающий среды: температура среды в процессе эксплуатации (Тc max), заданная ТУ; - внутреннее тепловое сопротивление элемента (компонента) или кристалла ИС (Rт вн, С/Вт): тепловое сопротивление самого элемента (компонента, кристалла) и тепловое сопротивление контакта между этим элементом (компонентом) и платой (кристаллом и корпусом) с учетом теплового сопротивления клеевой прослойки. Считается, что: - корпус изотермален, его температура во всех точках постоянна, - коэффициенты теплопроводности (i) всех материалов конструкции ИС не зависят от температуры в рассматриваемом диапазоне, - тепловыделяющие элементы ИС являются плоскими источниками тепла, - теплопередачей через газовую среду внутри корпуса и приволочные выводы можно пренебречь. В случае протяженного источника тепла, имеющего линейные размеры bхl (рис. 2.1,а в приложении), при l,b>>h весь тепловой поток сосредоточен под элементом ИС, плоскопараллелен и направлен к подложке: 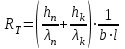 (2.1) (2.1)где n и k – коэффициенты теплопроводности материала подложки и клея соответственно, Вт /м С, hn и hk – толщина подложки и клеевого слоя, м, b и l – размеры контакта тепловыделяющего элемента с подложкой, м. Б) При малых линейных размерах источника тепла тепловой поток становится расходящимся (рис. 2.1,б), увеличивается эффективность теплоотвода и падает тепловое сопротивление, которое рассчитывается: 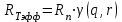 (2.2) (2.2)Где (q, r) – безразмерная функция поправок, значения которой определяются графиками (рис.2.2 в приложении): q = l / 2h r = b / 2h h = hn + hk Расчет значения RT или RТэфф по формулам (2.1-2.2) позволяет определить как перегрев элемента э, при известной рассеиваемой мощности Рэ, так и его температуру Тэ,: 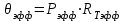 (2.3) (2.3)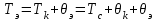 (2.4) (2.4)где Тс – температура окружающей среды, Тк – температура корпуса (Тк = Тс + к ), k – перегрев корпуса относительно температуры окружающий среды. Для определения температуры навесного дискретного компонента (Тнк) ГИС следует учитывать перегрев области p-n – перехода относительно подложки (вн): 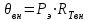 (2.5) (2.5) (2.6) (2.6)Расчет перегрева корпуса k , входящего в выражения (2.4) и (2.6), проводится при известных: конструкции корпуса, мощности рассеяния помещенных в корпус кристаллов или платы, способа монтажа ИС в составе узла или блока ИЭТ, способа охлаждения. Сначала определяют тепловое сопротивление корпуса Rк: 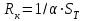 (2.7) (2.7)где – коэффициент теплопередачи, определяемый способом охлаждения, Вт/м2 С, SТ – площадь теплового контакта корпуса с теплоотводом, м2, Перегрев корпуса можно оценить: 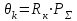 (2.8) (2.8)где Р – суммарная мощность, рассеиваемая ИС, Вт. Соотношение (2.4) не учитывает перегрева за счет взаимного влияния соседних тепловыделяющих элементов, то есть положения тепловых потоков всех источников тепла данной микросхемы. Этот эффект частично учтен значением k. Для обеспечения нормального по требованиям надежности теплового режима работы навесных компонентов и элементов ИС необходимо выполнение условий: 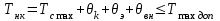 (2.9 а) (2.9 а)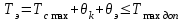 (2.9 б) (2.9 б)где Тс max – максимальная температура окружающий среды в процессе эксплуатации, задаваемая ТУ на прибор, Тmax доп – максимально допустимая рабочая температура элемента и компонента, оговариваемая в ТУ на компоненты или материалы пленочных элементов. Таблица 2.1. Исходные данные для теплового расчета фрагмента ГИС:
Расчёт температуры транзистора VT1 Рассчитаем тепловое сопротивление транзистора (2.1); считаем, что данный элемент – протяженный источник тепла. Зададим предварительно параметры: м м м м  При малых линейных размерах источника тепла увеличивается эффективность теплоотвода и падает тепловое сопротивление, которое рассчитывается по формуле (2.2): Найдем (q, r):   — тепловое сопротивление при малых линейных размерах источника тепла. Рассчитаем тепловое сопротивление корпуса, подставив известные значения в (2.7):  , где α0=300 Вт/м2 С (из условия), Оценим перегрев корпуса (2.8): °C Тогда температура корпуса равняется: Тк = Тс + к=50+19.048=69. 048 ˚C °C Далее определим перегрев элемента за счет рассеиваемой мощности, используем при этом формулу (2.3): °C По формуле (2.5) рассчитаем перегрев в области p-n-перехода: °C По формуле (2.6) с учётом всех параметров, рассчитанных выше, найдем температуру транзистора VT1: Как видно из расчетов, температура корпуса транзистора VT1 при заданных параметрах превышает максимально допустимую норму. Посмотрим внимательно на формулу расчета теплового режима навесного дискретного компонента и выявим, что наиболее всего влияет на конечный результат перегрев в области p-n-перехода вн. Так как мы не можем повлиять на мощность рассеяния в структуре заданного транзистора, попробуем снизить другие параметры путем изменения некоторых величин. В начальных условиях сказано, что транзистор и два резистора помещены в металлостеклянный корпус и посажены с помощью эпоксидного клея (h = 0.1 мм) на теплоотводящую шину ( = 300). Зададим другие параметры: вместо эпоксидного клея будем использовать компаунд с наполнителем (SiO2),теплопроводность которого равна 0,8 Вт/м2 С, также переместим фрагмент ГИС с платы на металлический теплоотвод, что повысит α до 105 Вт/м2 С. Сменим материал подложки — вместо поликора будем использовать бериллиевую керамику (n=210 Вт/м2 С) размерами 16х10 мм (тип корпуса – «Акация»). Повторим расчеты: При = 105 , SТ=18×10×10-6 м тепловое сопротивление корпуса: °C Тогда перегрев корпуса будет равен: Для расчета теплового сопротивления в случае протяженного источника тепла зададим предварительные параметры: м м Отсюда: Тепловой расчет при малых линейных размерах источника тепла ((q, r) остаётся прежним): °C Пересчитаем э с новыми значениями: °C Итак, найдем температуру навесного компонента с измененными параметрами: Были выбраны иные конструктивно-технологические условия процесса сборки и повторно проведен расчет, однако, не смотря на изменение условий, температурный режим работы транзистора КТ 380 не входит в заданные рамки. Напомним, что максимально допустимая рабочая температура элемента и компонента не должна превышать 85С. Рекомендации к использованию данного фрагмента ГИС: топология кристалла требует переработки, необходимо заменить используемый транзистор, так как его мощность рассеяния неприемлема в данных условиях, также как и внутреннее тепловое сопротивление. Был проведен расчет и определены допустимые значения для вновь выбранного навесного компонента: Допустим, С/Вт, тогда перегрев в области p-n-перехода будет равен: °C Проведем расчет: °C Таким образом, можно достигнуть нормального по требованиям надежности теплового режима работы. Расчёт температуры резистора R1 По формуле (2.1) рассчитаем тепловое сопротивление резистора R1, считая данный элемент протяжённым источником тепла: м м  Далее, по формуле (2.2) рассчитаем эффективное тепловое сопротивление корпуса R1. Для данного расчёта сначала необходимо определить по графику значение γR1(qR1,r R1).   По графику безразмерный поправочный коэффициент приблизительно будет равняться: °C Далее по формуле (2.3) рассчитаем перегрев компонента за счёт рассеиваемой мощности: По формуле (2.4) с учётом всех рассчитанных выше параметров рассчитываем температуру корпуса резистора R1: °C Как видно из расчётов, в данном случае получаем достаточно низкую температуру корпуса резистора R1. Расчёт температуры резистора R2 По формуле (2.1) рассчитаем тепловое сопротивление резистора R2, считая данный элемент протяжённым источником тепла: м м  Далее, по формуле (2.2) рассчитаем эффективное тепловое сопротивление корпуса R2. Для данного расчёта сначала необходимо определить по графику значение γR1(qR1,r R1).   По графику безразмерный поправочный коэффициент приблизительно будет равняться: Далее по формуле (2.3) рассчитаем перегрев компонента за счёт рассеиваемой мощности: ˚C По формуле (2.4) с учётом всех рассчитанных выше параметров рассчитываем температуру корпуса резистора R1: ˚C Как видно из расчётов, в данном случае получаем приемлемую температуру корпуса резистора R2. Вывод по результатам расчетов теплового режима гибридной ИС: несмотря на попытку оптимизировать параметры теплопередачи для обеспечения нормального по требованиям надежности теплового режима работы навесных компонентов, не удалось достигнуть нормального режима работы дискретного компонента. Были использованы все возможные типы корпусов, в расчетах указан наиболее удачный вариант; с конструкцией подобранного корпуса можно ознакомиться в приложении (рис.2.4), рассчитываемый фрагмент ГИС представлен на рис. 2.3. | |||||||||||||||||||||||||||||||||||||||||
