работа. Курсовая работа по дисциплине "Проектирование электрических фильтров"

• Название: Курсовая работа по дисциплине "Проектирование электрических фильтров"
• Анкор: работа
• Дата: 06.12.2021
• Размер: 101 Kb.
• Имя файла: work_95837_baa961d.doc
• Тип: Курсовая; #293505

Аннотация

Идрисов Загид Гаджиевич. Курсовая работа по дисциплине “Проектирование электрических фильтров”. ДГТУ ,РТФ, 221гр.

В курсовой работе проведены расчеты фильтра нижних частот Чебышева, полосового фильтра Чебышева и активного фильтра.

Расчеты сделаны с использованием таблиц, а также приведен аналитический расчет полюсов передаточной функции.

Пояснительная записка содержит 13 листов машинописного текста.

Электрические схемы представлены чертежами формата А4.

Введение

Электрические фильтры -это линейные 4-х полюсники, обладающие избирательными свойствами. Они предназначены для выделения из состава сложного электрического колебания, подведенного к его входу, частотных составляющих определенного спектра частот в заданной полосе частот с небольшим ослаблением и подавления тех составляющих, которые расположены в других, также заданных полосах частот.

Вся область частот от f=0 до f =∞ подразделяются на:

• Области, где ослабление не превышает некоторое заданное значение ослабления ∆А (полоса пропускания-ПП)

• Области, где ослабление не менее некоторого заданного значения А_s (полосы задерживания-ПЗ)

• Переходные области.

По заданному расположению полос пропускания и задерживания различают 4 типа фильтров:

• Фильтр верхних частот (ФВЧ)

• Фильтр нижних частот ФНЧ)

• Полосовые фильтры (ПФ)

• Режекторные фильтры (РФ).

При синтезе фильтров широко используется нормирование по сопротивлению и частоте. Здесь вводится понятие фильтра прототипа нижних частот. Один из способов синтеза фильтров является синтез на основе фильтра прототипа нижних частот. Рассчитав нормированные значения элементов этого фильтра, переходят с помощью преобразования к полосовым режекторным или фильтрам верхних частот. Переход от нормированных величин осуществляется с помощью коэффициентов нормирования. В курсовой работе рассчитываются фильтры с использование полиномов Чебышева и Баттерворта.

Анализ технического задания.

Министерство образования Российской Федерации.

Дагестанский государственный технический университет.

Радиотехнический факультет.

Кафедра РТ и БМЭ.

Курсовая работа по дисциплине « Проектирование электрических фильтров».

В курсовой работе, согласно варианта №58, необходимо рассчитать фильтры нижних частот, полосового фильтра и активного фильтра.

Исходными данными для расчета являются:

• 
  частота среза- f₁,
  
• 
  частота задерживания-f_s,
  
• 
  ослабление в полосе пропускания-∆A,
  
• 
  ослабление в полосе задерживания-A_s .
  

Согласно заданию необходимо провести два вида расчетов: табличный и аналитический.

Расчет проводится на основе фильтра прототипа нижних частот. Последовательность расчета:

1. 
   нормирование по частоте;
   
2. 
   определение порядка фильтра;
   
3. 
   расчет полюсов передаточной функции;
   
4. 
   расчет входного сопротивления;
   
5. 
   разложение входного сопротивления в цепную дробь;
   
6. 
   определение нормированных значений элементов;
   
7. 
   вычисление коэффициентов денормирования;
   

8.расчет истинных значений элементов.

Расчет активного фильтра сводится к определению передаточной функции ФНЧ. Здесь используем табличные коэффициенты. С помощью этих коэффициентов определяются элементы схемы.

1.Расчет фильтра нижних частот Чебышева.
Исходные данные:

• 
  Частота среза f₁=3кГц.
  
• 
  Частота задержки f_s=5кГц.
  
• 
  Ослабление в полосе пропускания ∆А=1дб.
  
• 
  Ослабление в полосе задержки A_s=16дб.
  

I.Расчет с помощью таблиц.

1. 
   нормирование частоты
   

Ω= f_s/ f₁ (1.1)

Ω=5/3=1.66

2. 
   расчет порядка фильтра
   

(1.2)

n=16+6-10*lg(10^0.1-1)/20*lg(1.66+1.66²-1)=2.93

округляем до целого числа n=3

3. 
   из таблицы9 [1] выписываем нормированные значения элементов LC- фильтра нижних частот:
   

c1=c3=2.024

l₂=0.994

4.определим коэффициенты денормирования для вычисления истинных значений элементов схемы:

K_l=R_Н/2*π*f* (1.3)

K_l=600/2*3.14*3*10³=31.8*10^-3Гн.

K_c=1/R_н*2*π*f (1.4)

K_c=1/600*2*3.14*3*10³=88.4*10^-8Ф.

4. 
   определяем истинные значения элементов:
   

C₁= C₃ = K_l* c₁=2.024*88.4*10^-9=178.9нФ. (1.5)

L₂= K_c* l₂=31.8*10^-3*0.994=31.6мГн. (1.6)
II. Аналитический расчет.

S_k=-γsin(2*k-1/2*n)*π+ ј*β*cos(2*k-1/2*n)*π (1.7),

Где γ=(ε-1/ε)/2 , β=(ε+1/ε)/2, ε= , ε=

γ=(1,34-1/1,34)/2=0,494; β=1.115

Расчет полюсов проводят для k=2*n=2*3=6 значений, и выбирают те значения, у которых вещественная часть отрицательная.

S₁= 0,494*sin((1/6)*3,14)+ j*1.115*co(s(1/6)*3,14)=0,247+j0.965

S₂ = 0,494*sin((3/6)*3,14)+ j*1.115*cos((3/6)*3,14)=0.494

S₃= 0,494*sin((5/6)*3,14)+ j*1.115*cos((5/6)*3,14)=0,247-j0.965

S₄=0,494*sin((7/6)*3,14)+ j*1.115*cos((7/6)*3,14)=-0,247-j0.965

S₅=0.494sin((9/6)*3,14 )+ ј*1.115*cos((9)/6)*3,14) = -0.494

S₆=0.494*sin((11/6)*3,14 )+ ј*1.115*cos((11)/6)*3,14) =-0.247+j0.965

Вычисляем полином Гурвица:

V(S)=П(S-S_k) (1.9)

Для этого выбираем те значения, у которых вещественная часть S_k отрицательная.

V(S)=(S- S₄)* (S- S₅)* (S- S₆) В результате подстановки получаем:

V(S)=(S+0.247-j0.965)*(S+0.247+j0.965)*(S+0.494)=

(S² +S*0.494+0.994)*(S+0.494)=S³+S²*0.988+S*1.28+0.491

Вычисляем нормированное входное напряжение:

Z _ВХ=V(S)-h(S)/ V(S)+h(S) (1.10),

где h(S) =S³+0.75S-функция фильтрации.

Z _ВХ=2S³ +0,988S²+1.238S+0,75S+0,491/ S² 0.988+1.238S+0,491-0.75S=

=2S³ +0,988S²+1.988S+0,491/ S² 0,988²+0,488S+0,491
а) делим числитель на знаменатель:

2 S³ +0.988S²+1,988S+0.491 0.988S²+0.488S+0.491

2S³+0.988S²+0.988S 2.024S

S+0.491-первый остаток

б) делим делитель на первый остаток

0.988S²+0.488S+0.491 S+0.491

0.988S²+0.488S 0.994S

0.491-второй остаток

в) делим второй делитель на второй остаток

S+0.491 0.491

S 2.024S

0.491-третий остаток

г) делим третий делитель на 3-й остаток

0,491:0,491=1
Таким образом, мы получили полное соответствие расчетных значений табличным значениям.

III Расчет ослабления фильтра.

A=10lg(1+(10^0.1*∆A-1)Ω²ⁿ)

Ослабление необходимо рассчитать на частотах:

f₀ =3.75*10³

f₁=3*10³

f_s=5*10³,

1,5f₁=4,5*10³

2f₁ =6*10³


A_f1 =10lg(1+(10^0,1-1)*1)=1дб

A_fs=16дб

A_f*1.5=10lg(1+(10^0.1-1)*1.5⁶)=4.68дб

A_f*2=10lg(1+(10^0.1-1)*2⁶)=12.7дб

A_f*0=1дб
Зависимость ослабления от частоты на рис.1.1.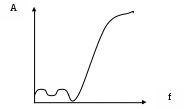



Рис.1.1.

Амплитудно-частотная характеристика в приложении.

Электрическая схема фильтра выполнена на формате А4.

2. Расчет полосового фильтра Баттерворта

Исходные данные:

• 
  Частота среза f₁ =14,4кГц
  
• 
  Частота задержки f_s2=16кГц
  
• 
  f₀=12кГц
  
• 
  Ослабление в полосе пропускания ∆А=2дб
  
• 
  Ослабление в полосе задержки A_s2=15дб.
  

Расчет.

1. 
   определим неизвестные частоты:
   
   • 
     частота среза f_s1
     
   • 
     частота среза f₁
     
   • 
     средняя частота f_0.
     

Так как, АЧХ фильтра симметричная, то ∆f₁ = f₁ -f₀ =14.4-12=2.4кГц

f_-1= f0-Δf ₁=12-2.4=9.6кГц.

∆f_s = f_s1+ f₁=16+14.4=1.6кГц

f_s2 = f_-1+ ∆f_s =9.6-1.6=8кГц

2. нормирование частоты

Ω= k(f_s/ f₀ - f₀/f_s) (2.1)

k= f₀ /( f₁- f_-1)-коэффициент преобразования полосы пропускания полосового фильтра

k=12/(14.4-9.6)=2.5

Ω=2.5*(16/12 -12/16)=1.45

3. расчет порядка фильтра

(2.2)

n=15-10lg(10^0.1*2-1)/20*lg1.45=5.37, округляем до n=6.

3. 
   Из таблицы10 [1] выписываем нормированные значения элементов LC- фильтра нижних частот.
   

c₁=0.5176

l₂=1.4142

c₃=1.9319

l₄=1.9319

c₅=1.4142

l₆=0.5176

4.Определим нормированные значения элементов полосового фильтра, используя преобразование:

l_i=kl_i, c_i=1/l_i (2.3)

l_i=1/kc_j, c_i=kc_j (2.4)

c_6п= l_1п=1/2.5*0.5176=0.772

c_4п= l_3п =1/2.5*1.9319=0.207

c_2п= l_5п =1/2.5*1.4142=0.282

c_5п= l_2п =2.5*1.4142=3.53

c_3п=l_4п =2.5*1.9319=4.82

c_1п=l_6п =2.5*0.5176=1.294

5.определим коэффициенты денормирования для вычисления истинных значений элементов схемы:

K_l=R_Н/2*π*f₀ (2.5)

K_l=600/2*3.14*12*10³=7,96*10^-3Гц.

K_c=1/R_н*2*π*f (2.6)

K_c=1/600*2*3.14*12*10³*=22.1*10^-8Ф.

5. 
   определяем истинные значения элементов:
   

L3=0.207*7.96*10^-3=1.64мГн

L1= K_l* l₁=0.772*7.96*10^-3=6.14мГн.

L5=0.282*7.96*10^-3=2,24мГн

L2=3,53*7.96*10^-3=28мГн

L4=4,82*7.96*10^-3=38,3мГн

L6=1,294*7.96*10^-3=10,3мГн

C₁= K_c* c₁=1,294*22,1*10^-9=28,5*10^-9Ф.

C3=4,82*22,1*10^-9=106,5*10^-9Ф.

C5=3,53*22,1*10^-9=78*10^-9Ф.

C2=0,282*22,1*10^-9=6,23*10^-8Ф.

C4=0,207*22,1*10^-9=4,57*10^-9Ф.

C6=0,772*22,1*10^-9=17,06*10^-9Ф.

6.Расчет ослабления фильтра.

А =10lg (1+(10^0,1*ΔА-1)*Т_n²(Ω)), где

Т_n(Ω)=ch(n*ArchΩ) здесь ArchΩ=ln(Ω+ Ω²-1)

f₀ =12*10³

f_-1=9,6*10³

f₁=14,4*10³

f_s2=16*10³,

1,5f_s2=24*10³

2f_s2 =32*10³
Вычислим Ω по формуле 2.1 и заносим данные в таблицу.

Ω	3,75	5,71	1,45	0,91	0
f	1,5fs2	2fs2	fs2	f1	f0
Af	32,1	43	20	2	0

Зависимость ослабления от частоты на рис.1.1.

50

40

30

20

10

9,6 12 14,4 16 24 32

Амплитудно-частотная характеристика в приложении.

Электрическая схема фильтра выполнена на формате А4.

2. Расчет активного фильтра Баттерворта нижних частот.

Исходные данные:

• 
  Частота среза f₁=25кГц.
  
• 
  Частота задержки f_s=50кГц.
  
• 
  Ослабление в полосе пропускания ∆А=1дб.
  
• 
  Ослабление в полосе задержки A_s=25дб.
  
• 
  Коэффициент усиления к=12
  

Расчет.

1. 
   нормирование частоты
   

Ω= f_s/ f₁ (3.1)

Ω=50/25=2

2. 
   расчет порядка фильтра
   

(3.2)

n=25-10lg(10^0.1*1-1)/20*lg2=5.

3. 
   Фильтр состоит из двух звеньев второго порядка. Коэффициент усиления:К=К1*К2=12 .
   

К1=2, К2=2, К3=1,25.

Коэффициенты первого звена (табл12. [1]):

В^/ =0,618 С^/ =1

Коэффициенты второго звена:

B^// =1,618 C^// =1

5. Определяем емкости конденсаторов первого звена:

С₂=10/ f₁ [мкФ] (3.3)

С₂=10/25*10³=0,4нФ.

С₁≤(В^/2+4С^/ (к-1))*С₂/4С^/ (3.4)

C₁≤((0,618²+4*(2-1))*0,4*10^-9)/4=0,43нФ.

4. 
   Вычисляем резистивные сопротивления первого звена: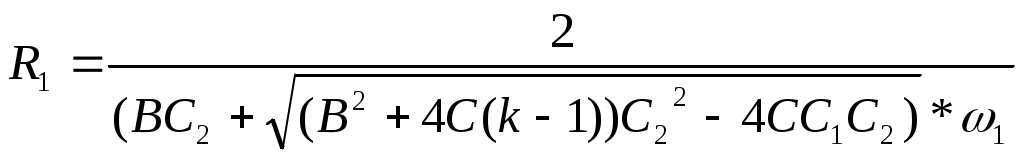
   

(3_.5)

R^/₁ =2/[0,618*0,4*10^-9+√(0,618²+4(2-1))*(0.4*10^-9)²-4*0,4*10^-9 *0,43*10^-9]*6,28*25*10³=35,2Ом

R^/₁ =35,2кОм.

R^/₂ =1/С*С₁С₂R₁w₁² (3.6)

R^/₂ =1/0,43*0,4*10^-18*35,2*10³*(6,28*25*10³)²=6,7кОм

R^/₃ =k(R₁+ R₂)/k-1

R^/₃ =2*(35,2+6,7)*10³/1=83,8кОм.

R^/₄ =k*(R1+R2)

R^/₄=2*(35,2+6,7)*10³=83,8кОм.

5. 
   Определяем емкости конденсаторов второго звена:
   

С₁≤(В^/2+4С^/ (к-1))*С₂/4С

C^//₁≤((1,618²+4*(2-1))*0,4*10^-9)/4=0,66нФ.

7. Вычисляем резистивные сопротивления второго звена:

R^//₁=2/[1,618*0,4*10^-9+√(1²+4(2-1))*(0.4*10^-9)²-4*0,66*10^-9*0,4*10^-9]*6,28*25*10³=9кОм

R^//₂ =1/0,4*0,66*10^-18*9*10³*(6,28*25*10³)²=17кОм

R^//₃=2(9+17)*10³/1=52кОм

R^/₄=2(9+17)*10³=52kOм.

8. Вычисляем сопротивления третьего звена:

R^///₁ =1/2*π*f₁*C1*C

R^///₁ =1/6.28*25*10³*0.4=15.9кОм

R^///₂ =к*R1/к-1=1,25*15,9/1,25-1=79,5кОм

R^///₃=к*R1=1.25*15.9=19.8кОм.

Амплитудно-частотная характеристика в приложении.

Электрическая схема фильтра выполнена на формате А4.

Список используемой литературы.

1. 
   Задание на курсовую работу и методические указания к ним по курсу «Теория электрических цепей» по теме электрические фильтры. Москва 1998. Составитель Щебес М.Р.
   
2. 
   Знаменский А.Е., Теплюк И.Н. Активные RC- фильтры. Связь. Москва 1970.
   
3. 
   Проектирование усилительных устройств. Под ред. Н.В.Терпугова.- М.Ж Высш. Школа, 1982.
   

Заключение

В курсовой работе представлен расчет трех видов фильтров: LС – фильтры нижних частот Чебышева, нагруженного двусторонне; симметричного полосового LC – фильтра Баттерворта, нагруженного двусторонне; активного RC – фильтра нижних частот Баттерворта.

Работа выполнена в полном объеме всем требованиям выполнения, которые предъявляют согласно методическим указаниям. В работе даны ответы на все поставленные задачи, с необходимыми к ним рисунками и графиками.

В ходе выполнения работы были использованы справочные данные по высшей математике, а также были использованы, предъявляемые к размерам элементов электрических схем. В целом выполнение курсовой работы не вызвало больших затруднений.