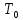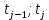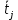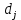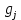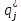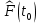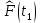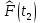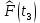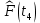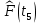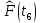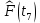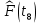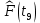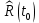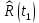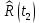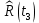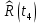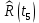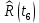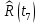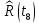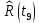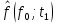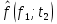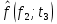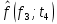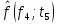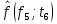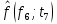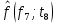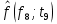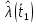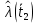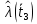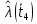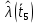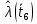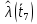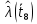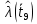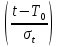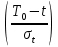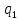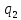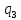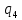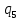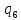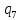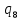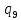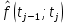Составление вероятностной модели распределения наработки технического объекта с целью возможности дальнейшего прогнозирования от. курсач чернышов. Курсовая работа по дисциплине Прогнозирование эксплуатационной надежности автотранспортных средств
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский Государственный технический университет» Факультет автомобильного транспорта Кафедра «Техническая эксплуатация и ремонт автомобилей» Курсовая работа по дисциплине «Прогнозирование эксплуатационной надежности автотранспортных средств» Тема: «Составление вероятностной модели распределения наработки технического объекта с целью возможности дальнейшего прогнозирования отказов и выработки ресурса» Выполнил: ст.гр. ТЭРА-2Н Матрёнин В.В. Номер зачетной книжки: 19102033 Проверил: доцент Чернышов К.В. Волгоград, 2020 Оглавление Исходные данные………………………………………………………………….3 Этап 1. Определение закона распределения наработки, основных функциональных зависимостей распределения наработки и показателей надежности первого элемента……………………………………………………4 Этап 2. Определение основных функциональных зависимостей и показателей надежности остальных элементов технического объекта……………………..24 Этап 3. Определение функции надежности технического объекта в целом и вероятности отказа объекта за время t* по структурной схеме надежности…37 Исходные данные Таблица 1 - Исходные данные (Вариант 13)
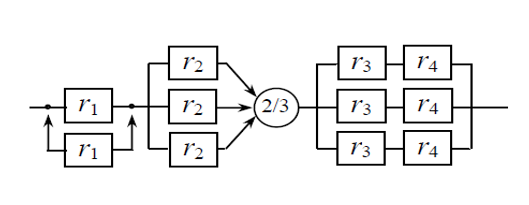 Рисунок 1 – Структурная схема надежности Этап 1. Определение закона распределения наработки, основных функциональных зависимостей распределения наработки и показателей надежности первого элемента Для построения графиков зависимостей заполним таблицу, где 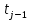 и и 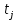 соответственно левая и правая границы j-го интервала времени, соответственно левая и правая границы j-го интервала времени, 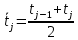 - середина j-го интервала, - середина j-го интервала, 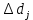 – количество отказавших объектов в j-м интервале времени, – количество отказавших объектов в j-м интервале времени, 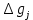 - количество объектов, выбывших из испытаний по каким-либо причинам в j-м интервале времени, - количество объектов, выбывших из испытаний по каким-либо причинам в j-м интервале времени, 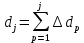 - суммарное количество отказов от начала испытаний до конца j-го интервала времени, - суммарное количество отказов от начала испытаний до конца j-го интервала времени, 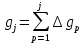 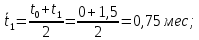 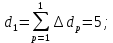 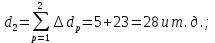 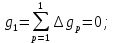 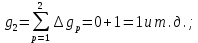 Эти величины являются исходными, подлежащими обработке. Для определения необходимых зависимостей используем метод Джонсона. Для каждого интервала определяется суммарное прогнозируемое количество отказов по формуле 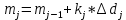 где 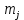 – прогнозируемое количество отказов к концу предыдущего интервала (для первого интервала – прогнозируемое количество отказов к концу предыдущего интервала (для первого интервала 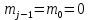 ); ); 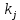 – коэффициент приращения отказа в j-м интервале – коэффициент приращения отказа в j-м интервале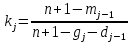 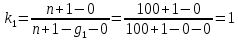 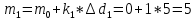 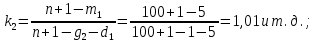 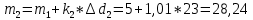 Далее вычислим прогнозируемое число отказов в каждом j-ом интервале 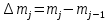 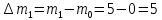 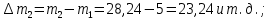 Зная значения 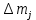 определим статистическое значение вероятности отказа (относительную частоту отказа) в каждом j-м интервале определим статистическое значение вероятности отказа (относительную частоту отказа) в каждом j-м интервале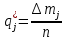 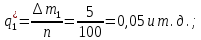 Таблица 2
Статистическую функцию распределения наработки строят на основании данных вариационного ряда по точкам, находящимся на границах интервалов этого ряда: 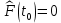 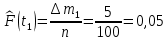 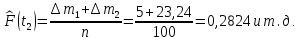 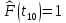 Таблица 3
Продолжение таблицы 3
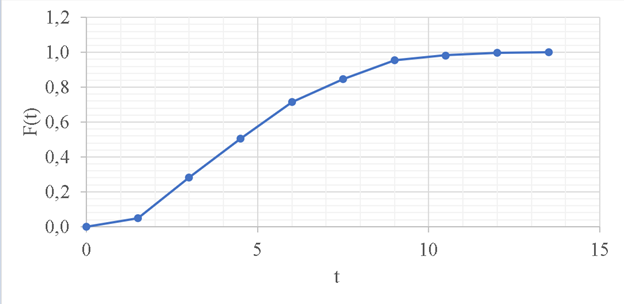 Рисунок 2 - График статистической функции распределения наработки При построении статистической функции надежности определяют значения функции надежности на границах интервалов ряда: 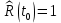 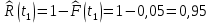 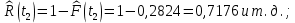 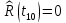 Таблица 4
Продолжение таблицы 4
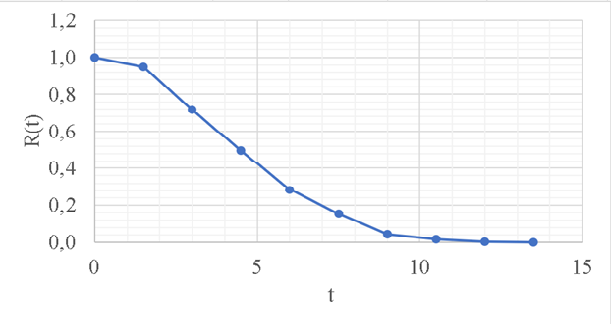 Рисунок 3 - График статистической функции надежности Гистограмма представляет собой статистический график плотности распределения наработки и поэтому строится как производная от графика функции распределения. Высота расположения j-го отрезка определяется по формуле 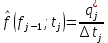 где 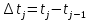 – величина j-го интервала. – величина j-го интервала.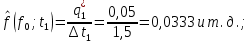 Таблица 5
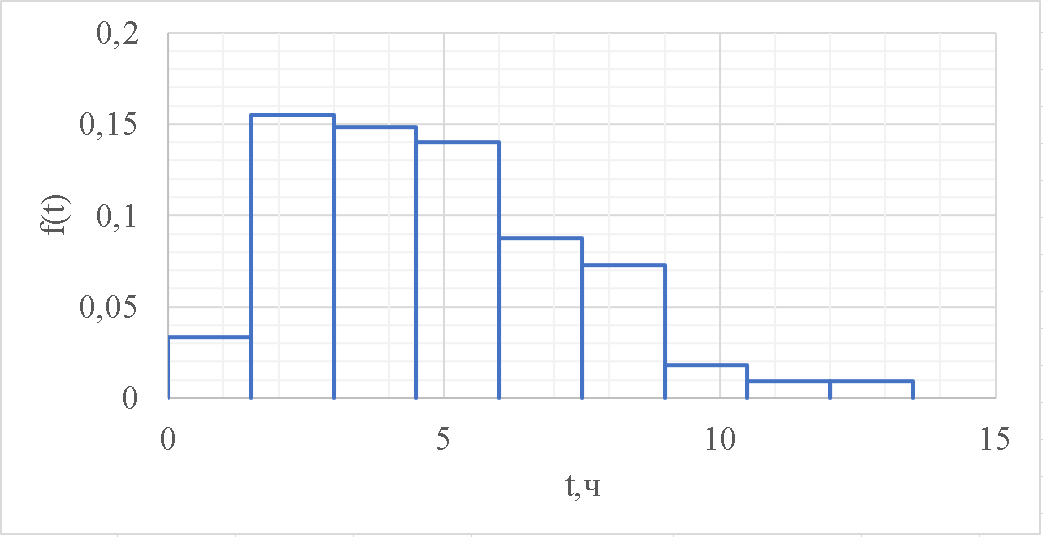 Рисунок 4 - Гистограмма распределения наработки Для построения графика статистической зависимости интенсивности отказов от времени в середине каждого интервала определяется значение интенсивности отказов по формулам 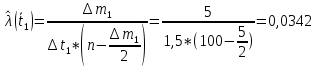 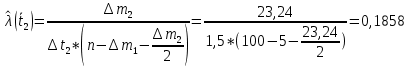 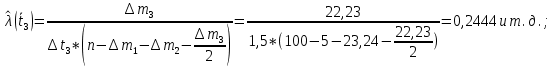 Таблица 6
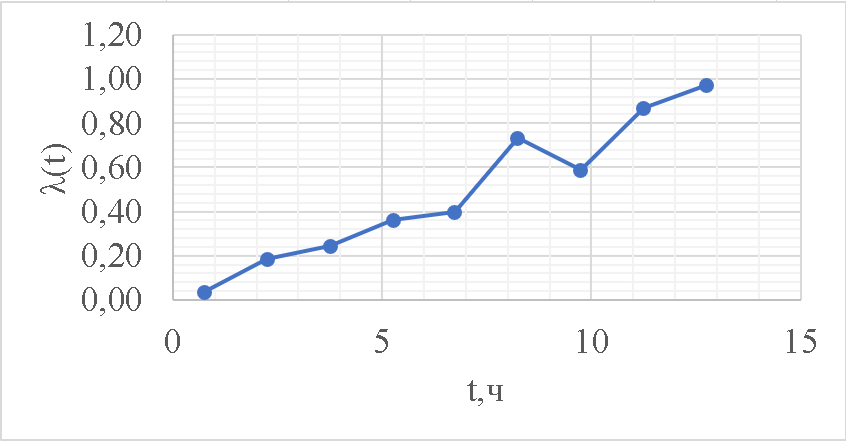 Рисунок 5 - График статистической функции интенсивности отказов По графикам зависимостей выдвигаем гипотезы о том, что это нормальное распределение или распределение Вейбулла. Определим параметры распределений. Нормальное распределение является двухпараметрическим распределениям. Параметрами нормального распределения являются средняя наработка (математическое ожидание наработки) T0 и среднеквадратическое отклонение 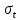 . .Оценку средней наработки можно определить на основе данных вариационного ряда по формуле 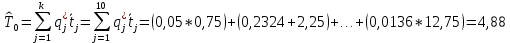 Дисперсию наработки объекта определим по формуле 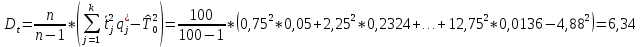 Оценка среднеквадратического отклонения находится по формуле 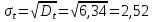 Распределение Вейбулла является двухпараметрическим распределением. Этими параметрами являются параметр формы η и параметр масштаба µ. Коэффициент вариации в случае распределения Вейбулла 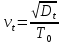 Где 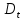 – дисперсия наработки объекта – дисперсия наработки объекта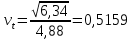 Используя метод моментов, приравняем статистическое значение коэффициента вариации 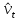 его точному значению его точному значению 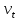 , по таблице зависимости ν(η) для распределения Вейбулла определим значение параметра формы , по таблице зависимости ν(η) для распределения Вейбулла определим значение параметра формы 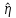 , соответствующее полученному значению , соответствующее полученному значению 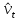 , а затем определим значение коэффициента масштаба с помощью формулы , а затем определим значение коэффициента масштаба с помощью формулы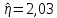 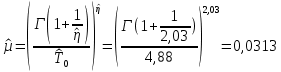 Подставляя полученные параметры в формулы временных зависимостей для соответствующих законов распределений, построим статистические графики. Нормальное распределение 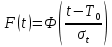 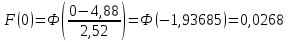 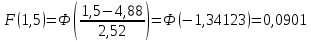 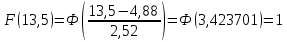 Таблица 7
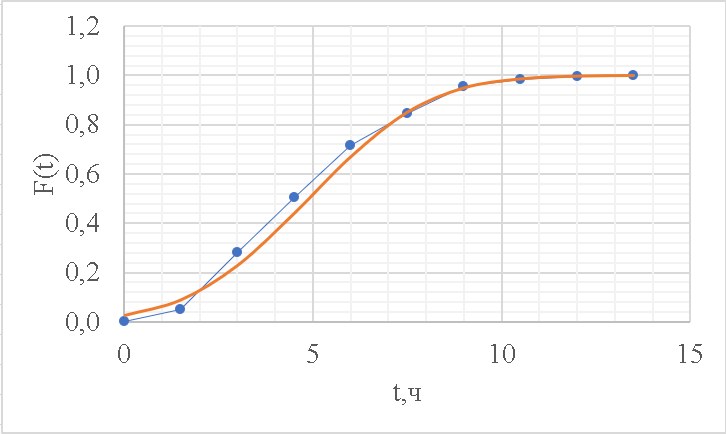 Рисунок 6 - Функция распределения наработки;  - - 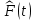 ; ;  - - 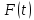 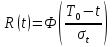 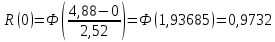 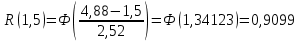 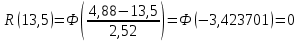 Таблица 8
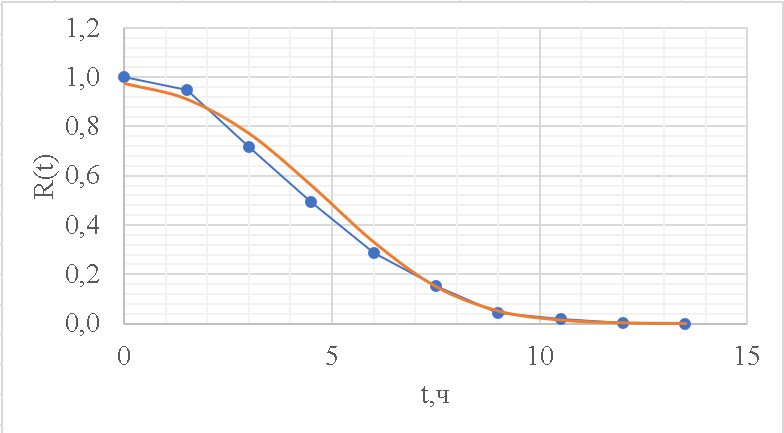 Рисунок 7 - Функция надежности;  - - 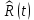 ; ;  - - 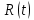 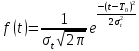 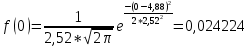 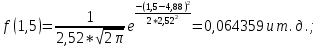 Таблица 9
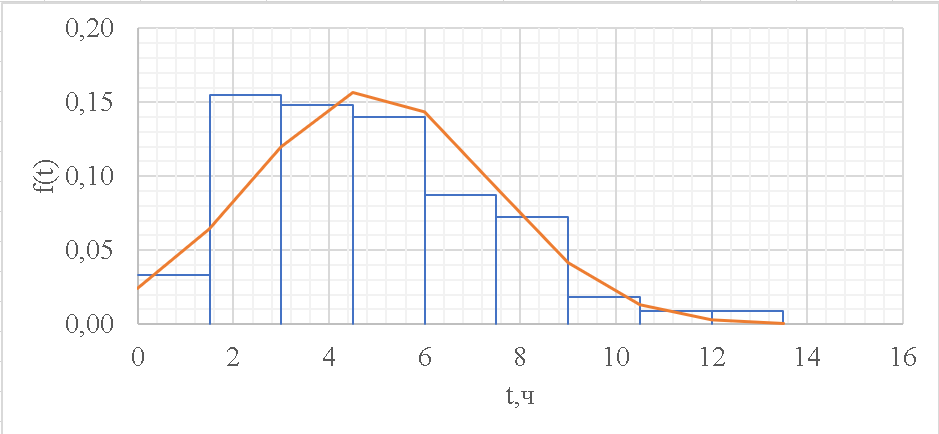 Рисунок 8 - Плотность распределения наработки;  - - 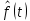 ; ;  - - 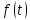 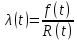 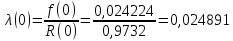 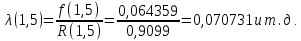 Таблица 10
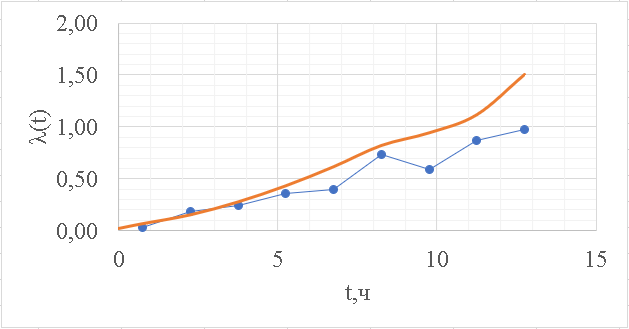 Рисунок 9 - Интенсивность отказов;  - - 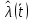 ; ;  - - 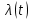 Оценим нормальный закон распределения с помощью критерия согласия Пирсона. В соответствии с критерием Пирсона, случайная величина 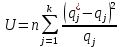 определяющая расхождение между теоретическим законом распределения и имеющимися статистическими данными, подчиняется закону 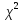 распределения с распределения с 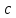 степенями свободы. Здесь степенями свободы. Здесь 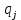 – вероятности отказов в соответствующих интервалах. Для нормального распределения – вероятности отказов в соответствующих интервалах. Для нормального распределения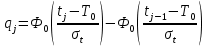  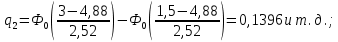 Таблица 7
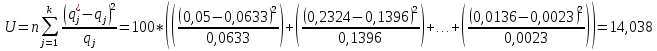 Число степеней свободы 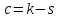 , где , где 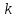 – это число интервалов статистического ряда, – это число интервалов статистического ряда, 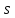 – число наложенных связей. Для нормального закона – число наложенных связей. Для нормального закона 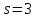 , тогда , тогда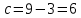 Используя таблицу квантилей 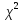 определяем, что вероятность данного распределения 0,025. определяем, что вероятность данного распределения 0,025.Распределение Вейбулла 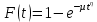 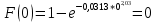 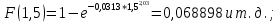 Таблица 8
Продолжение таблицы 12
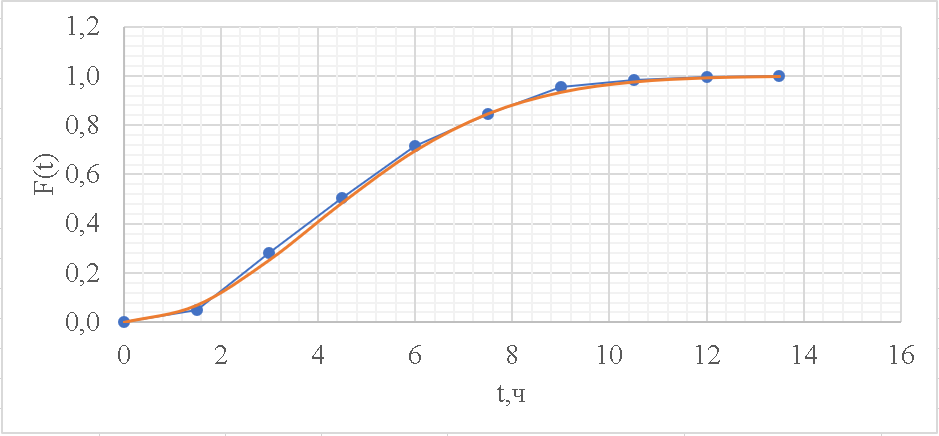 Рисунок 6 - Функция распределения наработки;  - - 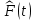 ; ;  - - 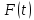 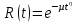 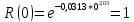 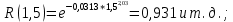 Таблица 9
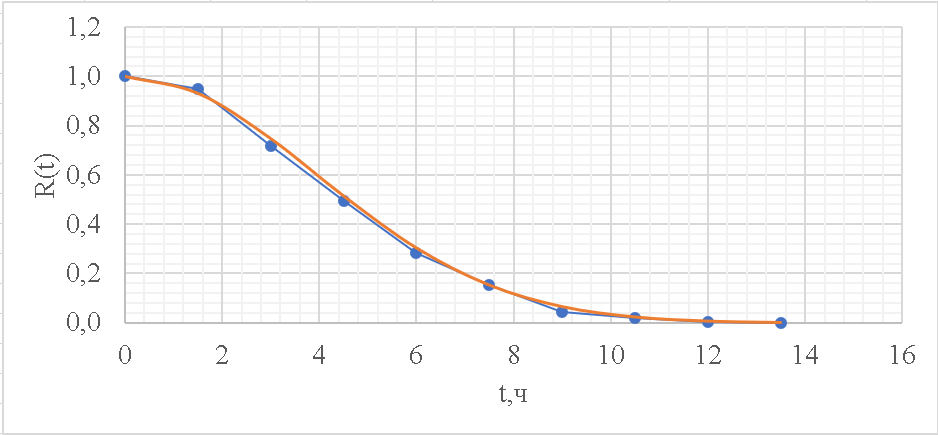 Рисунок 7 - Функция надежности;  - - 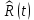 ; ;  - - 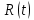 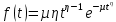 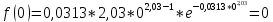 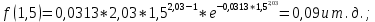 Таблица 10
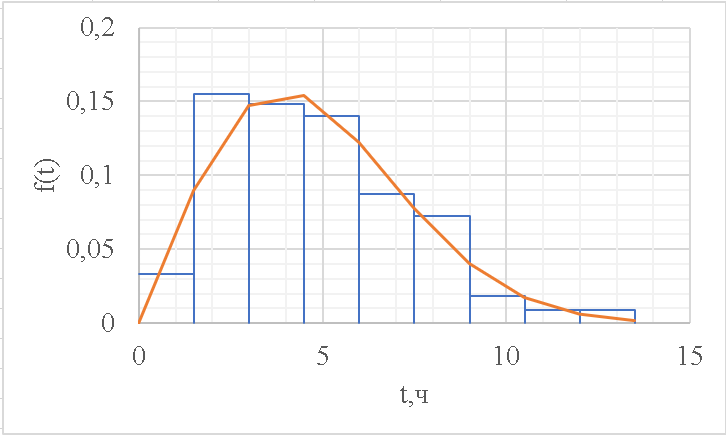 Рисунок 8 - Плотность распределения наработки;  - - 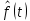 ; ;  - - 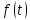 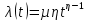 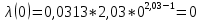 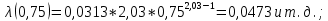 Таблица 11
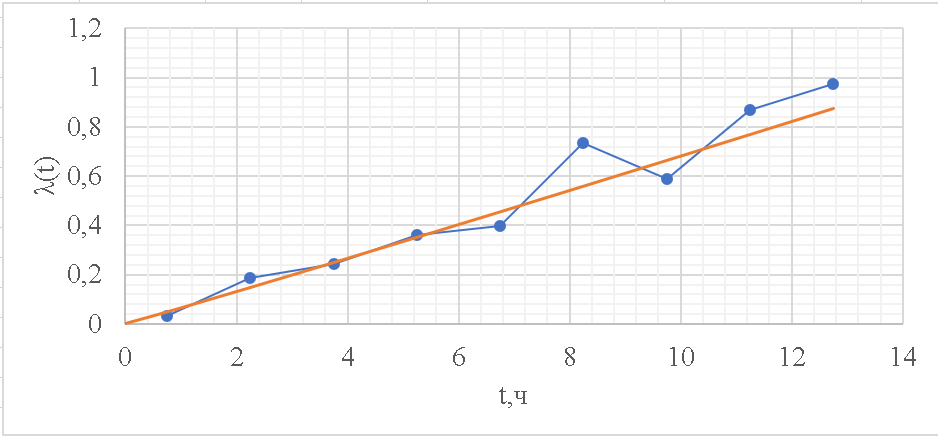 Рисунок 9 - Интенсивность отказов;  - - 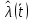 ; ;  - - 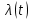 Оценим распределения Вейбулла с помощью критерия согласия Пирсона. 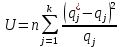 Для распределения Вейбулла 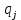 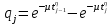 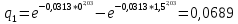 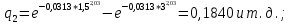 Таблица 12
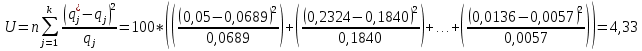 Для распределения Вейбулла 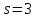 , тогда , тогда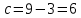 Используя таблицу квантилей 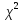 определяем, что вероятность данного распределения 0,57. определяем, что вероятность данного распределения 0,57.Большим уровнем значимости обладает распределение Вейбулла. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||