теплотехника. КР .docx04. Курсовая работа по дисциплине Теплотехника
 Скачать 103.34 Kb. Скачать 103.34 Kb.
|
|
Государственное образовательное учреждение высшего профессионального образования Уфимский государственный нефтяной технический университет Кафедра «Промышленная теплоэнергетика» Курсовая работа по дисциплине «Теплотехника»
Уфа 2021 ЗАДАНИЕ ДЛЯ ПЕРВОГО РАЗДЕЛА КУРСОВОЙ РАБОТЫ 1 кг газовой смеси в распределительной газовой сети (в емкости хранения сжиженных нефтяных газов, в газовом пространстве резервуара для нефти) в зависимости от состава совершает термодинамические процессы от состояния 1 до состояния 2 с показателями. Объем газовой смеси во всех процессах изменяется в раз. Смесь обладает свойствами идеального газа. Начальное (в состоянии 1) давление. Определить основные параметры газовой смеси в состоянии 1 и состоянии 2, изменение внутренней энергии, энтальпии, энтропии смеси, работу, внешнюю теплоту процесса, коэффициент распределения энергии в процессах. Исходные данные для варианта 04 принять по двум последним цифрам шифра зачетной книжки по табл. 2 и 3. Обработка исходных данных для газовой смеси. Смесь состоит из пяти индивидуальных газов. Нужно для каждого газа записать молярную массу. Данные имеются в пособии на стр. 58. Можно принимать округленно. Например, для метана μ(СН4)=16 г/моль (в таблице 16,04 г/моль). Определить объемные доли компонентов смеси. Для этого переводим объемную концентрацию из процентов в доли (делением на 100). Например, VСН4=80%, объемная доля - 0,8. Определить молярную массу газовой смеси по формуле, г/моль 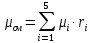 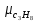 =12*3+1*8=44 г/моль =12*3+1*8=44 г/моль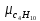 =12*4+1*10=58 г/моль =12*4+1*10=58 г/моль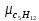 12*5+1*12=72 г/моль 12*5+1*12=72 г/моль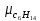 =12*6+1*14=86 г/моль =12*6+1*14=86 г/моль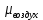 =28,96 г/моль =28,96 г/моль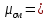 44*0.0002+58*0.1+72*0.088+86*0.01+29*0.80=36.20 г/моль 44*0.0002+58*0.1+72*0.088+86*0.01+29*0.80=36.20 г/мольГазовая постоянная смеси рассчитывается по формуле, кДж/(кг∙°С) Rсм =8,314/μсм Rсм =8,314/36.20=0.23 кДж/(кг∙°С) Массовые доли компонентов газовой смеси определятся для каждого из пяти газов 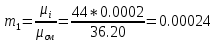 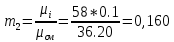 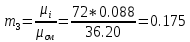 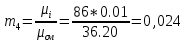  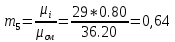 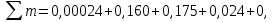 64 64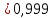 Сумма массовых долей должна быть равна единице. Начальный объем газовой смеси 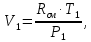 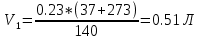 где Т1 абсолютная температура в градусах Кельвина. Конечный объем газовой смеси одинаков для всех процессов V2 = V1 ∙ ε, 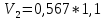 =0,56 Л =0,56 Лгде ε – степень сжатия – из исходных данных. Расчет процессов. Расчет изобарного процесса Показатель политропы n1=0 Давление в конце процесса, Па P2=P1 =140КПа Температура в конце процесса, К Т2= Т1∙ ε Т2=(37+273)*1,1=341К Средняя температура, К Тср=(Т1+Т2)/2 Тср=(341+310)/2=325,5К Или в градусах Цельсия tср= Тср – 273,15 tср=325,5-273,15=52,35 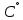 Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при средней температуре определяются для каждого из пяти газов. Для углеводородных газов (метан, этан, пропан и т.д.) по графикам из пособия (рисунки 1.14 – 1.19) по температуре в градусах Кельвина.. Для неуглеводородных газов (воздух, азот, кислород и т.д.) рассчитывается по формулам из Приложения 1.1 практического пособия. Например, для воздуха по формуле вначале определяется мольная теплоемкость где t = tср – средняя температура из предыдущего пункта, °С. Затем рассчитывается массовая теплоемкость воздуха делением мольной теплоемкости воздуха на молярную массу воздуха 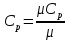 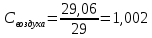 кДж/(кг∙°С) кДж/(кг∙°С)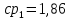 кДж/(кг∙°С) кДж/(кг∙°С)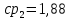 кДж/(кг∙°С) кДж/(кг∙°С)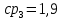 кДж/(кг∙°С) кДж/(кг∙°С)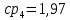 кДж/(кг∙°С) кДж/(кг∙°С)Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 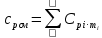 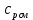 =1,86*0.0002+1,88*0.1+1,9*0.088+1,97*0.01+1,002*0.80=1,18 кДж/(кг∙°С) =1,86*0.0002+1,88*0.1+1,9*0.088+1,97*0.01+1,002*0.80=1,18 кДж/(кг∙°С)где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 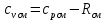 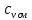 =1,18-0,23=0,95 кДж/(кг∙°С) =1,18-0,23=0,95 кДж/(кг∙°С) Показатель адиабаты k 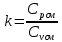 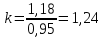 Термодинамическая работа процесса , кДж/кг l= P1 ∙ (V2-V1) l= 140 ∙ (0,56-0,51) = 7 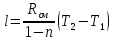 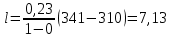 кДж/кг кДж/кгИзменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1) Δu =0,95*(341-310)=29,45 кДж/кг Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1) Δh=1,18*(341-310)=36,58 кДж/кг Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) 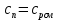 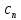 =1,18кДж/(кг∙°С) =1,18кДж/(кг∙°С) Теплота процесса, кДж/кг q = Δh q=36,58 кДж/кг Изменение удельной энтропии процесса, кДж/(кг ∙°С) 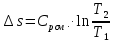 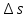 =1,18* =1,18*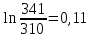 кДж /(кг ∙°С) кДж /(кг ∙°С)Расчет политропного процесса с n2 Показатель политропы n=n2=0,20 Давление в конце процесса, Па 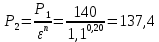 па паТемпература в конце процесса, К Т2= Т1/ ε(n-1) Т2= 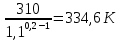 Средняя температура, К Тср=(Т1+Т2)/2 Тср=(334,6+310)/2=322,3К Или в градусах Цельсия tср= Тср – 273,15 tср=322,3-273,15=49,15 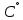 Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при средней температуре определяются для каждого из пяти газов. Для углеводородных газов (метан, этан, пропан и т.д.) по графикам из пособия (рисунки 1.14 – 1.19) по температуре в градусах Кельвина.. Для не углеводородных газов (воздух, азот, кислород и т.д.) рассчитывается по формулам из Приложения 1.1 практического пособия. Например, для воздуха по формуле вначале определяется мольная теплоемкость где t = tср – средняя температура из предыдущего пункта, °С. Затем рассчитывается массовая теплоемкость воздуха делением мольной теплоемкости воздуха на молярную массу воздуха 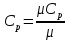 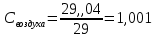 кДж/(кг∙°С) кДж/(кг∙°С)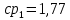 кДж/(кг∙°С) кДж/(кг∙°С)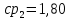 кДж/(кг∙°С) кДж/(кг∙°С)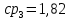 кДж/(кг∙°С) кДж/(кг∙°С)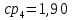 кДж/(кг∙°С) кДж/(кг∙°С)Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 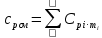 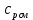 =1,77*0.0002+1,80*0.1+1,82*0.088+1,90*0.01+1,001*0.8=1,16кДж/(кг∙°С) =1,77*0.0002+1,80*0.1+1,82*0.088+1,90*0.01+1,001*0.8=1,16кДж/(кг∙°С)где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 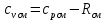 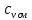 =1,16-0,23=0,93 кДж/(кг∙°С) =1,16-0,23=0,93 кДж/(кг∙°С) Показатель адиабаты k 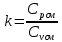 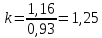 Термодинамическая работа процесса , кДж/кг l= P1 ∙ (V2-V1) l= 140 ∙ (0,56-0,51)=7 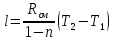 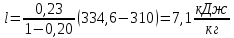 Изменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1) Δu =0,93*(334,6-310)=28,83 кДж/кг Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1) Δh=1,16*(322,3-310)=35,96кДж/кг Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) 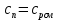 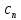 =1,16кДж/(кг∙°С) =1,16кДж/(кг∙°С) Теплота процесса, кДж/кг q = Δh q=35,96 кДж/кг Изменение удельной энтропии процесса, кДж/(кг ∙°С) 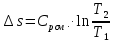 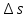 =1,16* =1,16*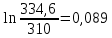 кДж/(кг ∙°С) кДж/(кг ∙°С)Расчет политропного процесса с n2 Показатель политропы n=n3 =1,0 Давление в конце процесса, Па 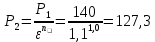 па паТемпература в конце процесса, К Т2= Т1/ ε(n-1) Т2= 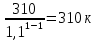 Средняя температура, К Тср=(Т1+Т2)/2 Тср=(310+310)/2=310К Или в градусах Цельсия tср= Тср – 273,15 tср=310-273,15=36,85 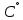 Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при средней температуре определяются для каждого из пяти газов. Для углеводородных газов (метан, этан, пропан и т.д.) по графикам из пособия (рисунки 1.14 – 1.19) по температуре в градусах Кельвина.. Для не углеводородных газов (воздух, азот, кислород и т.д.) рассчитывается по формулам из Приложения 1.1 практического пособия. Например, для воздуха по формуле вначале определяется мольная теплоемкость где t = tср – средняя температура из предыдущего пункта, °С. Затем рассчитывается массовая теплоемкость воздуха делением мольной теплоемкости воздуха на молярную массу воздуха 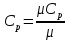 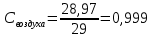 кДж/(кг∙°С) кДж/(кг∙°С)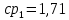 кДж/(кг∙°С) кДж/(кг∙°С)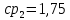 кДж/(кг∙°С) кДж/(кг∙°С)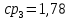 кДж/(кг∙°С) кДж/(кг∙°С)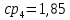 кДж/(кг∙°С) кДж/(кг∙°С)Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 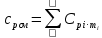 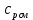 =1,71*0.0002+1,75*0.1+1,78*0.088+1,85*0.01+0,999*0.8=1,15кДж/(кг∙°С) =1,71*0.0002+1,75*0.1+1,78*0.088+1,85*0.01+0,999*0.8=1,15кДж/(кг∙°С)где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 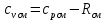 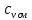 =1,15-0,23=0,92 кДж/(кг∙°С) =1,15-0,23=0,92 кДж/(кг∙°С) Показатель адиабаты k 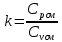 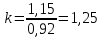 Термодинамическая работа процесса , кДж/кг l= P1 ∙ (V2-V1) l= 140 ∙ (0,56-0,51)=7 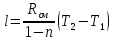 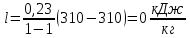 Изменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1) Δu =0,93*(310-310)=0 кДж/кг Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1) Δh=1,15*(310-310)=0 кДж/кг Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) 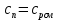 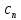 =1,15кДж/(кг∙°С) =1,15кДж/(кг∙°С) Теплота процесса, кДж/кг q = Δh q=l=7кДж/кг Изменение удельной энтропии процесса, кДж/(кг ∙°С) 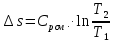 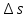 =1,15* =1,15*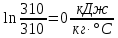 Расчет политропного процесса с n4 Показатель политропы n=n4 =1,10 Давление в конце процесса, Па 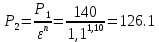 па паТемпература в конце процесса, К Т2= Т1/ ε(n-1) Т2= 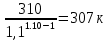 Средняя температура, К Тср=(Т1+Т2)/2 Тср=(307+310)/2=309К Или в градусах Цельсия tср= Тср – 273,15 tср=308.5-273,15=35.4 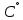 Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при средней температуре определяются для каждого из пяти газов. Для углеводородных газов (метан, этан, пропан и т.д.) по графикам из пособия (рисунки 1.14 – 1.19) по температуре в градусах Кельвина.. Для неуглеводородных газов (воздух, азот, кислород и т.д.) рассчитывается по формулам из Приложения 1.1 практического пособия. Например, для воздуха по формуле вначале определяется мольная теплоемкость где t = tср – средняя температура из предыдущего пункта, °С. Затем рассчитывается массовая теплоемкость воздуха делением мольной теплоемкости воздуха на молярную массу воздуха 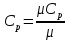 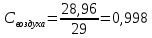 кДж/(кг ∙°С) кДж/(кг ∙°С)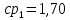 кДж/(кг ∙°С) кДж/(кг ∙°С)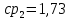 кДж/(кг ∙°С) кДж/(кг ∙°С)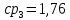 кДж/(кг ∙°С) кДж/(кг ∙°С)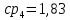 кДж/(кг ∙°С) кДж/(кг ∙°С)Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 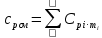 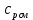 =1,7*0.0002+1,73*0.1+1,76*0.088+1,83*0.01+0,998*0.80=1,14кДж/(кг∙°С) =1,7*0.0002+1,73*0.1+1,76*0.088+1,83*0.01+0,998*0.80=1,14кДж/(кг∙°С)где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 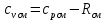 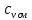 =1,14-0,23=0,91 кДж/(кг∙°С) =1,14-0,23=0,91 кДж/(кг∙°С) Показатель адиабаты k 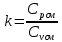 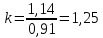 Термодинамическая работа процесса , кДж/кг l= P1 ∙ (V2-V1) l= 140 ∙ (0,56-0,51)=7 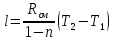 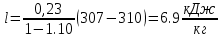 Изменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1) Δu =0,91*(307-310)=-2.73 кДж/кг Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1) Δh=1,14*(307-310)=-3.42кДж/кг Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) 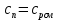 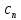 =1,14кДж/(кг∙°С) =1,14кДж/(кг∙°С) Теплота процесса, кДж/кг q = Δh q=-2.73кДж/кг Изменение удельной энтропии процесса, кДж/(кг ∙°С) 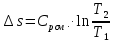 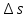 =1,14* =1,14*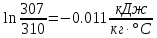 Расчет политропного процесса с n5 Показатель политропы n=n5 =k=1.25 Давление в конце процесса, Па 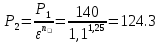 па паТемпература в конце процесса, К Т2= Т1/ ε(n-1) Т2= 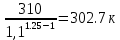 Средняя температура, К Тср=(Т1+Т2)/2 Тср=(302.7+310)/2=306.4К Или в градусах Цельсия tср= Тср – 273,15 tср=306.4-273,15=33.2 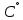 Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при средней температуре определяются для каждого из пяти газов. Для углеводородных газов (метан, этан, пропан и т.д.) по графикам из пособия (рисунки 1.14 – 1.19) по температуре в градусах Кельвина.. Для неуглеводородных газов (воздух, азот, кислород и т.д.) рассчитывается по формулам из Приложения 1.1 практического пособия. Например, для воздуха по формуле вначале определяется мольная теплоемкость где t = tср – средняя температура из предыдущего пункта, °С. Затем рассчитывается массовая теплоемкость воздуха делением мольной теплоемкости воздуха на молярную массу воздуха 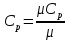 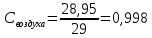 кДж/ (кг ∙°С) кДж/ (кг ∙°С)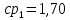 кДж/ (кг ∙°С) кДж/ (кг ∙°С)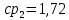 кДж/ (кг ∙°С) кДж/ (кг ∙°С)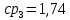 кДж/ (кг ∙°С) кДж/ (кг ∙°С)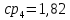 кДж/ (кг ∙°С) кДж/ (кг ∙°С)Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 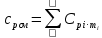 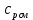 =1,7*0.0002+1,72*0.1+1,74*0.088+1,82*0.01+0,992*0.80=1,11кДж/(кг∙°С) =1,7*0.0002+1,72*0.1+1,74*0.088+1,82*0.01+0,992*0.80=1,11кДж/(кг∙°С)где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 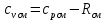 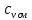 =1,11-0,23=0,88 кДж/(кг∙°С) =1,11-0,23=0,88 кДж/(кг∙°С) Показатель адиабаты k 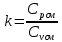 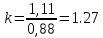 Термодинамическая работа процесса , кДж/кг l= P1 ∙ (V2-V1) l= 140 ∙ (0,56-0,51)=7 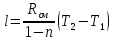 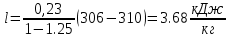 Изменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1) Δu =0,88*(306-310)=-3.52кДж/кг Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1) Δh=1,11*(306-310)=-4.44 кДж/кг Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) 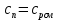 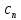 =1,11кДж/(кг∙°С) =1,11кДж/(кг∙°С) Теплота процесса, кДж/кг q = Δh q=-4.44кДж/кг Изменение удельной энтропии процесса, кДж/(кг ∙°С) 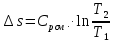 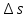 =1,11* =1,11*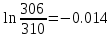 кДж/(кг ∙°С) кДж/(кг ∙°С)Часть 2 «Тепловой расчет теплообменного аппарата» Конструктивный тепловой расчёт ТОА Дано: 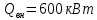 , , 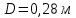 , , 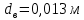 , , 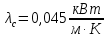 ; ;Мазут: 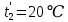 , , 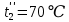 , , 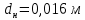 , , 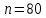 , , 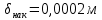 ; ;Вода: 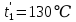 , , 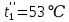 , , 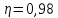 . .1. Тепловая мощность, полученная холодным теплоносителем, кВт 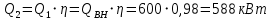 2. Построение графиков изменения температуры теплоносителей по длине аппарата: 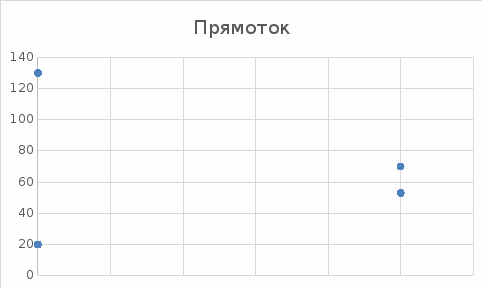 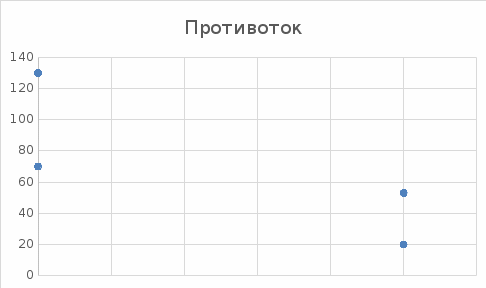 3. Температурные напоры для прямотока и противотока рассчитываются по формулам, °С Так как 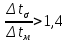 : , то по среднелогарифмической формуле : , то по среднелогарифмической формуле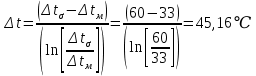 . .4. Изменение температуры по длине аппарата, °С 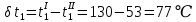 ; ;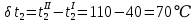 . .5. Средние температуры горячего и холодного теплоносителей, °С 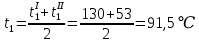 ; ;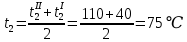 . .6. Физические свойства горячего и холодного теплоносителя определяются при средней температуре теплоносителей. Горячий теплоноситель Значения при средней температуре t1°С: средняя плотность 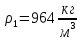 ; ;коэффициент теплопроводности 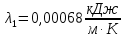 ; ;удельная теплоёмкость  ; ;кинематическая вязкость  ; ;коэффициент объёмного расширения  ; ;число Прандтля  . .Холодный теплоноситель Значения при средней температуре t2°С: средняя плотность 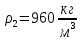 ; ;коэффициент теплопроводности 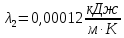 ; ;удельная теплоёмкость 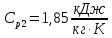 ; ;кинематическая вязкость 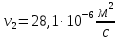 ; ;коэффициент объёмного расширения 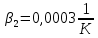 ; ;число Прандтля 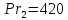 . .7. Проходные сечения для горячего и холодного теплоносителей, м2. Для горячего – площадь межтрубного пространства 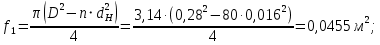 для холодного - площадь сечения трубок 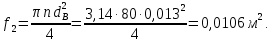 8. Скорости движения теплоносителей, м/с 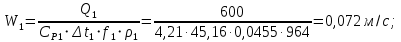 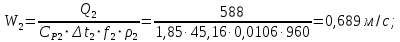 9. Эквивалентные диаметры, м 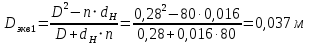 ; ;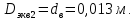 10. Число Рейнольдса для горячего и холодного теплоносителя: 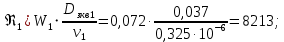 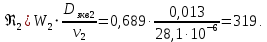 11. Температурный напор между жидкостью и стенкой, °С, рассчитывается, если Re<2300: 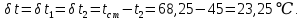 12. Числа Грасгофа для теплоносителей рассчитываются, если Re<2300: 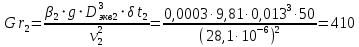 13. Задаемся температурой стенки (в первом приближении):  14. Физические свойства горячего и холодного теплоносителя при температуре стенки tст. Горячий теплоноситель Значения параметров при температуре стенки tст : средняя плотность  ; ;коэффициент теплопроводности  ; ;удельная теплоёмкость  ; ;кинематическая вязкость 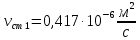 ; ;коэффициент объёмного расширения 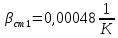 ; ;число Прандтля 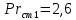 . .Холодный теплоноситель Значения параметров при температуре стенки tст : средняя плотность 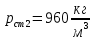 ; ;коэффициент теплопроводности 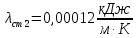 ; ;удельная теплоёмкость 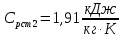 ; ;кинематическая вязкость 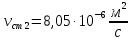 ; ;коэффициент объёмного расширения 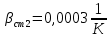 ; ;число Прандтля  . .15. Определим режимы течения и выберем формулу и рассчитаем число Нуссельта для горячего и холодного теплоносителей. Уравнение подобия при вынужденном течении однофазного теплоносителя по трубам и каналам имеет вид: при ламинарном вязкостном течении (Reж,d < 2300, Grж,d·Pr ж < 8·105)  при переходном течении (Reж,d = 2300…104)  16. Коэффициенты теплоотдачи для горячего и холодного теплоносителей, Вт/(м2∙°С)  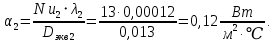 17. Коэффициенты теплопередачи, Вт/(м2∙°С) Толщина стенки трубок: 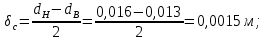 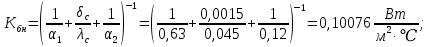 . .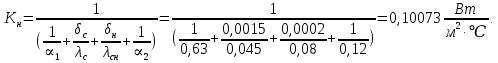 18. Определим площадь поверхности теплообмена, м2 для противотока  19. Плотность теплового потока (для противотока), Вт/м2  20. Полученная температура стенки (для противотока), °С  21. Полученная температура стенки отличается от заданной более, чем на 5 °С, приняв новую температуру стенки, равную полученной (  ), возвращаемся в пункт 13 для уточнения расчета. ), возвращаемся в пункт 13 для уточнения расчета. 21.13. Задаемся температурой стенки: 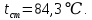 21.14. Физические свойства горячего и холодного теплоносителя при температуре стенки tст. Горячий теплоноситель Значения параметров при температуре стенки tст : средняя плотность 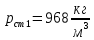 ; ;коэффициент теплопроводности 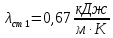 ; ;удельная теплоёмкость 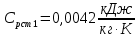 ; ;кинематическая вязкость  ; ;коэффициент объёмного расширения  ; ;число Прандтля  . .Холодный теплоноситель Значения параметров при температуре стенки tст : средняя плотность  ; ;коэффициент теплопроводности 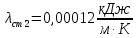 ; ;удельная теплоёмкость 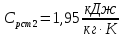 ; ;кинематическая вязкость 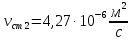 ; ;коэффициент объёмного расширения 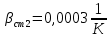 ; ;число Прандтля 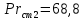 . .21.15. Определим режимы течения и выберем формулу и рассчитаем число Нуссельта для горячего и холодного теплоносителей. Уравнение подобия при вынужденном течении однофазного теплоносителя по трубам и каналам имеет вид: при ламинарном вязкостном течении (Reж,d < 2300, Grж,d·Pr ж < 8·105) 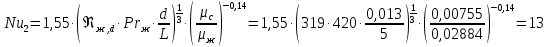 при переходном течении (Reж,d = 2300…104) 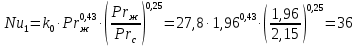 21.16. Коэффициенты теплоотдачи для горячего и холодного теплоносителей, Вт/(м2∙°С) 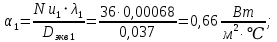 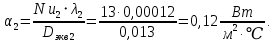 21.17. Коэффициенты теплопередачи, Вт/(м2∙°С) Толщина стенки трубок: 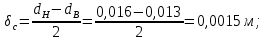 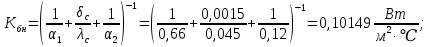 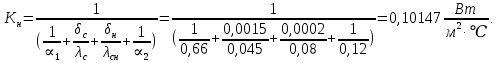 21.18. Определим площадь поверхности теплообмена, м2 для противотока  21.19. Плотность теплового потока (для противотока), Вт/м2  21.20. Полученная температура стенки (для противотока), °С  22. Средняя площадь теплообмена для одного погонного метра пучка труб ТОА  23. Суммарная длина пучка определяется для противотока и прямотока, а также с накипью и без накипи (рассчитываются 4 длины)  24. Определяются число секций теплообменного аппарата. Строится эскиз аппарата для варианта с наибольшим числом секций.   ЛИТЕРАТУРА Нащокин В.В. Техническая термодинамика и теплопередача. – М.: Высшая школа, 1980. – 469 с. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. – М.: Энергия, 1975. – 488 с. Болгарский А.В., Мухачев Г.А., Щукин В.К. Термодинамика и теплопередача. – М.: Высшая школа, 1964. – 459 с. Михеев М.А., Михеева И.М. Основы теплопередачи. – М.: Энергия, 1977. – 344 с. Краснощеков Е.А., Сукомел А.С. Задачник по теплопередаче. – М.: Энергия, 1969. – 254 с. Левин В.М., Шубин Е.П. Теплообменные аппараты систем теплоснабжения. – М.: Энергия, 1965. – 272 с. Кутателадзе С.С., Боришанский В.М. Справочник по теплопередаче. – М.: Госэнергоиздат, 1959. – 244 с. Расчеты основных процессов и аппаратов нефтепереработки: Справочник / Г.Г. Рабинович, П.М. Рябых, П.А. Хохряков и др. / Под ред. Е.Н. Судакова. – М.: Химия, 1979. – 568 с. |
